Static buoyancy

An object weighs less when it is immersed in a liquid - depending on the mass of the displaced liquid, the weight is reduced in accordance with the Archimedean principle .

The static buoyancy (in liquids and hydrostatic lift , in gases aerostatic buoyancy ) is the phenomenon that a body which in a quiescent fluid is immersed (liquid or gas), apparently loses weight. It looks as if the body has become lighter, it can even be "pulled up". In other words: its weight is partially, completely or excessively compensated by the static buoyancy force (also known as the hydrostatic buoyancy force ).

The (hydro) static buoyancy is often equated with the (hydro) static buoyancy force , although buoyancy actually only describes the effect that is created by the force .

Is the weight of the body is greater than the currently acting buoyancy, the body decreases in the fluid from . In the jargon of the Navy this is also negative buoyancy or negative buoyancy called, for example, in negative buoyancy cells of submarines. Is the weight force smaller, so the body increases in the fluid on . A movement driven by buoyancy ends when the buoyancy force and weight have found a new balance. For example, a hot air balloon rises until it has reached a layer of air with a lower density, which causes less buoyancy and has the same density as the balloon. When the forces are in equilibrium, the balloon floats without any change in altitude. A submarine that appears to the surface of the water can achieve equilibrium by partially leaving the water and thereby reducing its buoyancy. The submarine floats on the surface.

The strength of the static buoyancy results from the Archimedes' principle , i.e. it depends on the weight that has acted on the fluid that has now been displaced. The density of the body is often compared with that of the fluid in order to make a statement about the sinking, floating or rising of the body. The relation to the specific gravity of the fluid is out of date .

If fluid flows around objects , dynamic lift can also act (which, if it is directed downwards as contact pressure , is also referred to as downforce ), this dynamic lift is the physical principle for flying birds, airplanes and helicopters.

Physical background

The force of the water on the bottom (b) is greater than the force of the water on the top (a). The lateral forces (c) and (d) cancel each other out. They are irrelevant for buoyancy.

See also : Archimedes' principle

The buoyancy force of a body immersed in a fluid comes from the fact that the pressure of a fluid in the gravitational field , the so-called hydrostatic pressure , increases with depth, so it is different for each expanded body "below" and "above" . For example, is immersed parallelepipedic body with its base in a fluid, the hydrostatic pressure on the bottom surface (in the image b in) is greater than at the top ( a ). In the case of irregularly shaped bodies, the static buoyancy force is the force resulting from the (vertical) force components of the hydrostatic pressures that act on all parts of the surface.

Based on the submerged cuboid, one can derive: A buoyancy force acts on a body that is immersed in a fluid with the density : ${\displaystyle \rho }$ ${\displaystyle F_{\mathrm {A} }}$

${\displaystyle F_{\mathrm {A} }=g\rho V}$

It is the displaced by the body volume of the fluid, the Erdfallbeschleunigung . ${\displaystyle V}$ ${\displaystyle g}$

The product of density and volume is the mass of the fluid displaced by the body. And is its weight . The static buoyancy force thus corresponds to the weight of the fluid which would be in place of the immersed body. ${\displaystyle \rho V}$ ${\displaystyle m}$ ${\displaystyle g\rho V}$

${\displaystyle F_{\mathrm {A} {\text{, Körper}}}=F_{\mathrm {G} {\text{, Fluid}}}}$

This relationship is known as the Archimedean principle .

If the static buoyancy force is compared with the weight of the body under consideration, then the ratio of the densities of body and fluid is decisive for this comparison. It can be summarized in such a way that a body floats in a fluid when its mean density is exactly the same as that of the surrounding fluid, that it rises at a lower density or sinks at a higher density. ${\displaystyle {\vec {F}}_{\mathrm {A} }}$ ${\displaystyle {\vec {F}}_{\mathrm {G} }}$

The hydrostatic paradox states that the pressure only depends on the depth and not on the shape of a fluid. Therefore, the buoyancy force is independent of the amount of fluid in which the body is immersed. The principle therefore also applies if the remaining liquid has a smaller volume than the submerged part of the float.

The buoyancy force is smaller than the weight force: sinking

See also : Weighing value  and Dasymeter

• 

  Dasymeter at normal air pressure: Both bodies seem to have the same mass

• 

  Dasymeter in a vacuum: Due to the lack of buoyancy, the two bodies of unequal density are no longer in equilibrium

• 

  Zeppelin during the landing maneuver (1936), to balance water ballast (front) is drained

A buoyancy force acts on every body not only when immersed in a swimming pool, this is also the case in air. Under normal circumstances, this effect is much smaller (~ factor 1000) than in a liquid, but for precise weighing it must be taken into account that when determining the mass in air, only the weighing value is obtained as an approximate value . Even with small bodies such as oil droplets in air, the buoyancy must be taken into account for precise measurements of the balance of forces, see Millikan experiment .

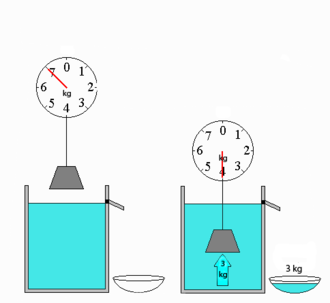
According to legend, Archimedes of Syracuse was supposed to check the gold content of a crown by dipping the crown and then a gold bar of the same weight into a full water container and measuring the amount of overflowing water. Galileo Galilei suspected that Archimedes instead used a beam balance, similar to the one shown above, to measure density differences due to different buoyancy in the water.

The buoyancy is greater than the weight: ascending

• 

  Vapor-containing smoke gases rise because they are buoyant in the cold (and denser) ambient air

• 

  Fire of moist leaves in open combustion (without chimney effect ) results in cooler smoke gases that are heavier due to soot and show little buoyancy

• 

  When Rhine flood 1993 of the floating shell located Schürmann-Bau (foreground) in increased ground water on the building stood out in places up to 70 centimeters.

• Hot air and gas balloons as well as airships rise when their mean density is less than that of the surrounding air. This is achieved either with a lifting gas with a lower density than air or with heated air. Warm air also has a lower density than the surrounding air. If the inner air filling in a hot air balloon cools down, the balloon sinks until the air is warmed up again. Vertical acceleration caused by buoyancy ends when buoyancy and weight are in equilibrium. For example, a hot air balloon rises until it has reached a layer of air with the same average density as the entire balloon (including the load). In the resulting equilibrium of forces, the balloon floats without any change in height. When a submarine appears on the surface of the water, equilibrium is established by lifting itself out of the water so far that the buoyancy force resulting from the displacement of the water is equal to the weight. The submarine then floats on the surface.
• With natural convection, differences in density cause gravity circulation, which was used in the (outdated) gravity heating .
• Scuba divers tare with the help of a buoyancy compensator that can be filled with a compressed air cylinder. Filling the buoyancy compensator increases buoyancy and the diver ascends. Since the water pressure continues to decrease as the diving depth decreases, the buoyancy compensator expands (due to the compressibility of the air) and the diver ascends even faster. In order not to be driven to the surface of the water, air must be released from the BC. Breathing the compressed air also leads to a change in the volume of the upper body. This effect can also be used for taring on a smaller scale.
• Volcanism , geysers or mud pots are based on buoyancy effects, just like the rising of vapor bubbles from the bottom of a vessel when a liquid is heated from below when it is boiled .
• Buildings with basements are threatened by buoyancy when the groundwater level is high . A house with a watertight basement made of reinforced concrete can float when the water rises. That is why such basements are sometimes deliberately flooded when flooded. Empty swimming pools can also float in the then elevated groundwater. In flood of heating oil tank in the flooded tank room can float, tilt, wires can be torn off and lick.
• Spaetzle or dumplings will rise to the top in the saucepan if the enclosed, now heated air causes an increase in volume and thus a decrease in density. This shows that they are completely heated and that they are done.
• CO ₂ bubbles in sparkling wine rise because of the buoyancy.

The lift force is equal to the weight

Hover

• 

  Solar balloon

• When a person floats in water (in a floating tank ) or drifts on the surface as a “dead man” , then he experiences roughly the same as in weightlessness . In this state of levitation the weight appears to be zero. For this reason, space travelers prepare for weightlessness in pools of water and practice work there that they have to carry out, for example, outside the space station or space shuttle .
• Submarines : During static diving , ballast tanks are deliberately flooded. This allows a submarine to be held at a certain depth.

Swimming on the surface

Because of the higher salt content in the Dead Sea , the density of the water is higher than in the North Sea , for example , which leads to a lower sinking depth due to the same buoyancy.

If, in addition to its weight, only the static buoyancy acts on a resting, partially submerged body (e.g. a ship) , then the buoyancy force in static equilibrium applies ${\displaystyle {\vec {F}}_{\mathrm {G} }}$ ${\displaystyle {\vec {F}}_{\mathrm {A} }}$

${\displaystyle {\vec {F}}_{\mathrm {A} }=-{\vec {F}}_{\mathrm {G} }}$

regardless of the density of the water, which however has an influence on the depth of penetration of the body (in equilibrium ) ${\displaystyle {F_{\mathrm {A} }}/{({\bar {\rho }}V)}={\bar {g}}}$

The so-called swimming equilibrium states that:

${\displaystyle {\frac {\text{Eintauchendes V}}{\text{Gesamtvolumen}}}={\frac {\text{Dichte d. schwimmenden Körpers}}{\text{Dichte der Flüssigkeit}}}}$

Use: draft of ships

Floating ships are in a stable equilibrium: If they dive deeper in high waves, the displaced water volume and thus the buoyancy increase and they are lifted up again. If they are lifted too far, the displaced water volume and buoyancy decrease, and gravity lets them submerge again.

If a ship heels to one side, e.g. B. in turning circle or cross wind, the draft increases on this side, while it decreases on the other side. According to the changed pressure conditions, the center of lift shifts and a moment arises that counteracts the heeling and brings the ship back into its starting position as soon as the external influence subsides.

→ Main article : Draft

If a ship is loaded, its weight increases, so it sinks deeper into the water and displaces more water than when it is unloaded. Because of the greater sinking depth, more buoyancy force acts , this is always in balance with the (now greater) weight force .

If this ship drives from the North Sea to the Elbe and thus changes from salt water to fresh water (which has a lower density than salt water), the buoyancy force would decrease in fresh water with unchanged immersion depth. Therefore, the ship sinks deeper until the buoyancy force of the larger sink volume is again in equilibrium with the weight of the ship.

Freeboard mark (left) and loading mark (right) on a ship: TF = Freeboard in fresh water tropics
F = Freeboard in fresh water
T = Freeboard in tropical sea water (salt water of the sea)
S = Summer loading mark in sea water
W = Freeboard in sea water in winter
WNA = Freeboard in Sea water in winter in the North Atlantic

Loading tags on ships indicate the (permitted) immersion depths in water of different densities. The top two horizontal upper edges of the step (towards the circular) freeboard mark for fresh water in inland waters, four lower one below the other for the denser salt water in the seas with different temperatures.

Rising methane bubbles of submarine methane hydrate on storage sites, this can for shipping dangerous. Scottish scientists attribute this to the sinking of a fishing trawler discovered in the Witches' Hole in the North Sea . The rising gas bubbles can therefore reduce the density of the sea ​​water so much that ships suddenly lose their ability to swim.

Application: density measurement, temperature measurement

A buoyancy force also acts on a hydrometer (also called a density spindle) that is immersed in a liquid with the same density : ${\displaystyle \rho }$ ${\displaystyle F_{\mathrm {A} }}$

${\displaystyle F_{\mathrm {A} }=g\rho V}$

The depth of penetration can therefore be used to determine the density of the liquid and thus possibly the content of dissolved substances, which can be read off on a scale adapted to the purpose of the hydrometer. A typical example of this is the scale aerometer .

In a liquid thermometer according to Galileo Galilei , the buoyancy bodies arranged in accordance with the temperature dependent density of the fluid in different heights in the respective position of equilibrium

A Galileo thermometer shows the temperature of the liquid based on the buoyancy of different bodies in a liquid. The glass spheres used for this purpose, whose diameter is larger than half the inner diameter of the cylinder (so that they stay in the stratification and do not "overtake" each other), were balanced with liquids in such a way that their mean density increases from the top sphere to the bottom sphere . Since the density of the liquid is temperature dependent, the buoyancy changes according to the temperature. At a certain temperature, all spheres rise up, the mean densities of which are smaller than the mean density of the liquid surrounding them. All spheres sink, the mean densities of which are greater than the mean density of the surrounding liquid. The current temperature can be read from the sticker attached to the ball floating at the bottom. If the liquid then heats up, i.e. its density decreases, another ball sinks and the new temperature can be read off the sticker attached to the ball floating at the bottom.

The effect of buoyancy, which changes with temperature, also occurs during submarine dives, when the temperature of the sea water decreases with increasing water depth or the submarine alternates between a warm and a cold sea current during static diving.

See also the illustration of the ship loading marks above, which take into account the different buoyancy of ships in summer and winter and in the cold waters of the North Atlantic and in warmer tropical waters.

Application: physical toys

• Cartesian diver
• Lava lamp

See also

• Fluid statics
• Aerostatics
• Isostasis

Web links

Wiktionary: Buoyancy  - explanations of meanings, word origins, synonyms, translations

Commons : Static Buoyancy  - collection of images, videos, and audio files

• Derivation of the buoyancy force from the pressure of gravity at student level ( LEIFI )

Individual evidence

1. ↑ Ernst Lecher: Mechanics and acoustics - heat - optics. ISBN 3-11-121275-0 , p. 121 ( limited preview in Google Book Search), last accessed in February 2020.
2. ↑ Joseph H. Spurk: Fluid Mechanics. ISBN 3-540-61308-0 , p. 143 ( limited preview in Google Book Search), last accessed in February 2020.
3. ↑ currents. P. 12 ( limited preview in Google Book search), last accessed in February 2020.
4. ↑ Physics and radio technology for seafarers. P. 48 ( limited preview in Google Book search), last accessed in February 2020.
5. ^ ^{A b c} Douglas C. Giancoli: Physics. ISBN 3-86894-023-5 , p. 460 ( limited preview in Google book search)
6. ↑ These buildings became much more expensive than planned ; at weser-kurier.de
7. ↑ Hans-Joachim Schlichting (physics teacher)
8. ↑ Hans-Joachim Schlichting (physics teacher)
9. ↑ David Halliday, Robert Resnick, Jearl Walker: Halliday Physics. ISBN 978-3-527-81260-8 , p. 467 ( limited preview in Google Book Search), last accessed in February 2020.
10. ^ Clifford A. Pickover: Archimedes to Hawking . Oxford University Press USA - OSO, 2008, ISBN 978-0-19-533611-5 , pp. 41 .
11. ^ Theodor Pöschl: Swimming the body . In: Textbook of hydraulics for engineers and physicists . Springer, Berlin / Heidelberg 1924, ISBN 978-3-642-98315-3 , p. 27–35 , doi : 10.1007 / 978-3-642-99127-1_4 ( springer.com [accessed February 25, 2020]).
12. ↑ Wolfgang Demtröder: Experimentalphysik 1 (=  Springer textbook ). Springer, Berlin / Heidelberg 2018, ISBN 978-3-662-54846-2 , doi : 10.1007 / 978-3-662-54847-9 ( springer.com [accessed February 25, 2020]).
13. ^ Johow, E. Foerster: calculation and design of the ships . In: Aid book for shipbuilding . Springer, Berlin / Heidelberg 1928, ISBN 978-3-642-50392-4 , p. 1–150 , doi : 10.1007 / 978-3-642-50701-4_1 ( springer.com [accessed February 25, 2020]).
14. ↑ ^{a b} Thomas Krist: Hydraulics . In: formulas and tables basic knowledge of technology . Vieweg + Teubner Verlag, Wiesbaden 1997, ISBN 978-3-528-14976-5 , p. 197–208 , doi : 10.1007 / 978-3-322-89910-1_16 ( springer.com [accessed February 25, 2020]).
15. ↑ BBC News: North Sea wreck in methane mystery. November 29, 2000 (accessed July 23, 2013).
16. ↑ Hans-Joachim Schlichting (physics teacher)
17. ↑ ^{a b} Games, Physics and Fun. P. 87 ( limited preview in Google Book search).