Principal shear stress

The principal shear ^stress ( dimension ML ⁻¹ T ⁻² , SI unit Pascal = N · m ⁻² , symbol τ ) is a term from strength theory . In a given state of stress , the greatest principal shear stress is also the maximum shear stress and, according to the shear stress hypothesis, this is responsible for the failure of a material.

The main shear stresses have the values

${\displaystyle \tau _{1}={\frac {|\sigma _{2}-\sigma _{3}|}{2}},\quad \tau _{2}={\frac {|\sigma _{3}-\sigma _{1}|}{2}},\quad \tau _{3}={\frac {|\sigma _{1}-\sigma _{2}|}{2}}.}$

In the plane stress state, the main shear stress is

${\displaystyle \tau _{\max }={\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}.}$

Here, σ _{1,2,3 are} the principal stresses and ( σ _x , σ _y , τ _xy ) is a plane stress state in the xy plane . The main shear stresses occur in sectional planes , the normals of which are an angle bisector of the corresponding main stress directions.

Mohr's circle of tension

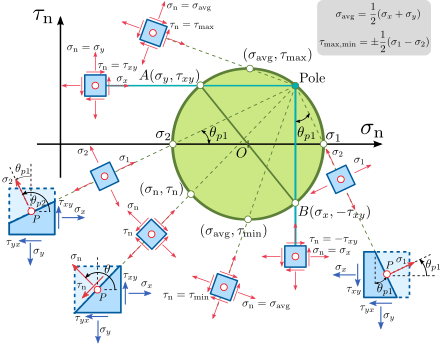
Mohr's circle of tension with sketches of various states of tension seen from the pole

The Mohr stress circle provides a clear orientation for the directions of the normals in which the main shear stresses occur . In the stress space, the normal stresses are plotted in a Cartesian coordinate system on the abscissa and the shear stresses on the ordinate . For a given stress state ( σ _x , σ _y and τ _xy ) the points A ( σ _y , τ _xy ) and B ( σ _x , - τ _xy ) define the endpoints of the diameter of the Mohr stress circle. Its intersection points with the abscissa indicate the principal stresses σ _1,2 and the points T with horizontal tangents provide the principal shear stress . The pole is the point P ( σ _x , τ _xy ). The angle between the abscissa and the segment (PT) shows the angle by which the current cutting plane with the given cutting stresses must be rotated in order for the main shear stress to occur. The same applies to the directions from the pole to the points of intersection of the circle with the abscissa and the principal stresses, see picture.

Flow area according to Tresca, Coulomb, Saint-Venant, Guest

Flow site area according to Tresca viewed along the room diagonal. Stress states can only be in the blue hexagon.

In the main stress space, in which the main stresses are plotted on the coordinate axes, each stress state occupies a point which also defines the main shear stresses. According to the shear stress hypothesis , it is the maximum principal stress difference, i.e. twice the greatest principal shear stress τ , that determines the plasticity of a material. The stress states, which have a maximum principal stress difference smaller than 2 τ , cause elastic deformation and lie in a prismatic body with a regular, hexagonal cross-section, see picture. Increasing or decreasing pressure in the material does not affect the main stress differences, because the pressure adds up to all three main stresses equally and is therefore emphasized in the difference formation. Therefore, the flow location area is infinitely extended in the direction of the space diagonal.

The flow location surface according to the shape change hypothesis forms the cylinder surrounding the prism, which is indicated in green in the picture.

Derivation in the plane stress state

Stresses on a cut triangle in a plane stress state

A plane stress state in the xy-plane is considered in which the shear stresses τ _xz and τ _yz vanish. The normal stress σ _z perpendicular to the plane does not necessarily have to be zero here.

Equilibrium in the triangle delivers, see picture:

${\displaystyle {\begin{aligned}\sum F_{ix}=&0=A\sigma _{\alpha }\cos \alpha +A\tau _{\alpha }\sin \alpha -A\sigma _{x}\cos \alpha -A\tau _{xy}\sin \alpha \\\sum F_{iy}=&0=A\sigma _{\alpha }\sin \alpha -A\tau _{\alpha }\cos \alpha -A\tau _{xy}\cos \alpha -A\sigma _{y}\sin \alpha \end{aligned}}}$

Where A is the length of the hypotenuse. With the double-angle functions from the fact, the voltages at the charge hypotenuse to

${\displaystyle {\begin{aligned}\sigma _{\alpha }=&{\frac {\sigma _{x}+\sigma _{y}}{2}}+{\frac {\sigma _{x}-\sigma _{y}}{2}}\cos 2\alpha +\tau _{xy}\sin 2\alpha \\\tau _{\alpha }=&{\frac {\sigma _{x}-\sigma _{y}}{2}}\sin 2\alpha -\tau _{xy}\cos 2\alpha \end{aligned}}}$

The maximum shear stress is also determined

${\displaystyle {\begin{aligned}{\frac {\partial \tau _{\alpha }}{\partial \alpha }}=&{\frac {\sigma _{x}-\sigma _{y}}{2}}2\cos 2\alpha +\tau _{xy}2\sin 2\alpha =0\\\rightarrow {\frac {\sin 2\alpha }{\cos 2\alpha }}=&\tan 2\alpha ={\frac {\sigma _{y}-\sigma _{x}}{2\tau _{xy}}}\\\rightarrow \tau _{\alpha }=&{\frac {\sigma _{x}-\sigma _{y}}{2}}{\frac {\tan 2\alpha }{\sqrt {1+\tan ^{2}2\alpha }}}-\tau _{xy}{\frac {1}{\sqrt {1+\tan ^{2}2\alpha }}}=-{\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}\\\rightarrow \tau _{\max }=&{\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}={\frac {|\sigma _{1}-\sigma _{2}|}{2}}\end{aligned}}}$

The latter results from the principal stresses

${\displaystyle \sigma _{1,2}={\frac {\sigma _{x}+\sigma _{y}}{2}}\pm {\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}.}$

The angle to the main stress directions results when they lie in the x or y direction:

${\displaystyle {\frac {\partial \tau _{\alpha }}{\partial \alpha }}={\frac {\sigma _{1}-\sigma _{2}}{2}}2\cos 2\alpha +\tau _{12}2\sin 2\alpha =(\sigma _{1}-\sigma _{2})\cos 2\alpha =0}$

Accordingly, either both principal stresses are the same and the shear stress disappears at all values ​​of α or the angle α = 45 ° defines an angle bisector of the principal stress directions, which are at α = 0 ° and α = 90 °.

Derivation in the three-axis stress state

A stress state is given with the principal stresses σ _1,2,3 and their principal stress directions, which define a Cartesian coordinate system with 1, 2 and 3 directions. The internal stresses on a cutting plane with normal unit vector with components n _1,2,3 then reads:

${\displaystyle {\vec {T}}^{({\hat {n}})}:={\begin{pmatrix}\sigma _{1}&&\\&\sigma _{2}&\\&&\sigma _{3}\end{pmatrix}}{\begin{pmatrix}n_{1}\\n_{2}\\n_{3}\end{pmatrix}}={\begin{pmatrix}\sigma _{1}n_{1}\\\sigma _{2}n_{2}\\\sigma _{3}n_{3}\end{pmatrix}}.}$

The shear component of this vector remains when the normal stress ${\displaystyle {\vec {s}}}$

${\displaystyle \sigma :={\vec {T}}^{({\hat {n}})}\cdot {\hat {n}}=\sigma _{1}n_{1}^{2}+\sigma _{2}n_{2}^{2}+\sigma _{3}n_{3}^{2}}$

is deducted:

${\displaystyle {\vec {s}}:={\vec {T}}^{({\hat {n}})}-({\vec {T}}^{({\hat {n}})}\cdot {\hat {n}}){\hat {n}}={\begin{pmatrix}\sigma _{1}n_{1}-\sigma n_{1}\\\sigma _{2}n_{2}-\sigma n_{2}\\\sigma _{3}n_{3}-\sigma n_{3}\end{pmatrix}}={\begin{pmatrix}(\sigma _{1}-\sigma )n_{1}\\(\sigma _{2}-\sigma )n_{2}\\(\sigma _{3}-\sigma )n_{3}\end{pmatrix}}.}$

Of this, the amount is the shear stress in the plane: . The square of the amount of the shear component should become stationary under the secondary condition . This secondary condition is taken into account with a Lagrange multiplier in the objective function: ${\displaystyle \tau :=|{\vec {s}}|}$ ${\displaystyle n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1}$

${\displaystyle {\begin{aligned}\Pi (n_{1},n_{2},n_{3},\lambda ):=&{\vec {s}}\cdot {\vec {s}}-\lambda (n_{1}^{2}+n_{2}^{2}+n_{3}^{2}-1)\\=&(\sigma _{1}-\sigma )^{2}n_{1}^{2}+(\sigma _{2}-\sigma )^{2}n_{2}^{2}+(\sigma _{3}-\sigma )^{2}n_{3}^{2}-\lambda (n_{1}^{2}+n_{2}^{2}+n_{3}^{2}-1)\to {\text{stat.}}\end{aligned}}}$

At a stationary point, the derivative of the objective function for each variable vanishes . The derivation requires the fulfillment of the secondary condition as desired. The derivative according to the components of the normals gives with : ${\displaystyle {\tfrac {\partial \Pi }{\partial \lambda }}=-(n_{1}^{2}+n_{2}^{2}+n_{3}^{2}-1){\stackrel {\displaystyle !}{=}}0}$ ${\displaystyle {\tfrac {\partial \sigma }{\partial n_{1}}}=2\sigma _{1}n_{1}}$

${\displaystyle {\begin{aligned}{\frac {\partial \Pi }{\partial n_{1}}}=&-2(\sigma _{1}-\sigma ){\frac {\partial \sigma }{\partial n_{1}}}n_{1}^{2}+2(\sigma _{1}-\sigma )^{2}n_{1}-2(\sigma _{2}-\sigma ){\frac {\partial \sigma }{\partial n_{1}}}n_{2}^{2}-2(\sigma _{3}-\sigma ){\frac {\partial \sigma }{\partial n_{1}}}n_{3}^{2}-2\lambda n_{1}\\=&2[(\sigma _{1}-\sigma )^{2}-2\sigma _{1}\underbrace {(\sigma _{1}n_{1}^{2}+\sigma _{2}n_{2}^{2}+\sigma _{3}n_{3}^{2})} _{=\sigma }+2\sigma \sigma _{1}\underbrace {(n_{1}^{2}+n_{2}^{2}+n_{3}^{2})} _{=1}-\lambda ]n_{1}\\\rightarrow {\frac {1}{2}}{\frac {\partial \Pi }{\partial n_{1}}}=&[(\sigma _{1}-\sigma )^{2}-\lambda ]n_{1}{\stackrel {\displaystyle !}{=}}0\\{\frac {1}{2}}{\frac {\partial \Pi }{\partial n_{2}}}=&[(\sigma _{2}-\sigma )^{2}-\lambda ]n_{2}{\stackrel {\displaystyle !}{=}}0\\{\frac {1}{2}}{\frac {\partial \Pi }{\partial n_{3}}}=&[(\sigma _{3}-\sigma )^{2}-\lambda ]n_{3}{\stackrel {\displaystyle !}{=}}0\end{aligned}}}$

The last two equations are derived analogously. The three components n _1,2,3 cannot all vanish at the same time due to the secondary condition. There are therefore (1) one, (2) two or (3) no components n _1,2,3 equal to zero.

If (1) only one normal component is zero, for example n ₂ = 0, then the problem is reduced to a plane:

${\displaystyle {\begin{aligned}1=&n_{1}^{2}+n_{3}^{2}\\\sigma =&\sigma _{1}n_{1}^{2}+\sigma _{3}n_{3}^{2}=\sigma _{1}n_{1}^{2}+\sigma _{3}(1-n_{1}^{2})\\\lambda =&(\sigma _{1}-\sigma )^{2}=(\sigma _{3}-\sigma )^{2}\end{aligned}}}$

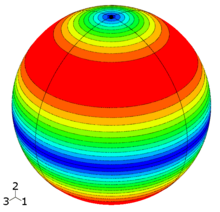
Amount of the shear stresses in the tangential planes of a sphere for the principal stresses σ ₁ = σ ₃ = 2 and σ ₂ = 0 from blue = 0 to red = 1

If σ ₁ - σ = σ ₃ - σ , then σ = σ ₁ = σ ₃ and . The main shear stress ${\displaystyle \tau ^{2}=(\sigma _{1}-\sigma )^{2}n_{1}^{2}+(\sigma _{3}-\sigma )^{2}n_{3}^{2}=0}$

${\displaystyle \tau =\tau _{2}={\frac {|\sigma _{1}-\sigma _{3}|}{2}}=0}$

lies on a circular ring with , the blue ring in the picture. In the other case, σ ₁ - σ = - ( σ ₃ - σ ), we get: ${\displaystyle n_{1}^{2}+n_{3}^{2}=1}$

${\displaystyle {\begin{aligned}\sigma _{1}-\sigma =&\sigma _{1}-\sigma _{1}n_{1}^{2}-\sigma _{3}n_{3}^{2}=\sigma -\sigma _{3}=\sigma _{1}n_{1}^{2}+\sigma _{3}n_{3}^{2}-\sigma _{3}\\\rightarrow 0=&(\sigma _{1}-\sigma _{3})(1-2n_{1}^{2})\end{aligned}}}$

The identity σ ₁ = σ ₃ has already been dealt with above. If the second factor disappears, then, because of the secondary condition, it follows and ${\displaystyle n_{1}=n_{3}={\tfrac {1}{\sqrt {2}}}}$ ${\displaystyle \sigma ={\tfrac {\sigma _{1}+\sigma _{3}}{2}}}$

${\displaystyle {\begin{aligned}\tau ^{2}=&(\sigma _{1}-\sigma )^{2}n_{1}^{2}+(\sigma _{3}-\sigma )^{2}n_{3}^{2}=\left({\frac {\sigma _{1}-\sigma _{3}}{2}}\right)^{2}\\\rightarrow \tau =&\tau _{2}={\frac {|\sigma _{1}-\sigma _{3}|}{2}}\end{aligned}}}$

If (2) two components of the normal are zero, then the normal lies in the direction of a principal stress direction and the shear component is zero, i.e. in the global minimum.

If (3) all three components are present, then at least two principal stresses must be equal. If all three principal stresses are equal, then there is a hydrostatic stress state and there are no shear stresses in any plane, which is nevertheless in accordance with the formulas for the principal shear stresses given at the beginning. If not all three principal stresses are equal, for example σ ₁ = σ ₃ ≠ σ ₂ , then and from the condition of the inequality of the remaining principal stresses,, follows and therefore . The secondary condition then delivers . The normal and principal shear stress are then ${\displaystyle \lambda =(\sigma _{1}-\sigma )^{2}=(\sigma _{2}-\sigma )^{2}=(\sigma _{3}-\sigma )^{2}}$ ${\displaystyle \sigma =\sigma _{2}n_{2}^{2}+\sigma _{1}(1-n_{2}^{2})}$ ${\displaystyle \sigma _{1}-\sigma =-(\sigma _{2}-\sigma )}$ ${\displaystyle (\sigma _{1}-\sigma _{2})(1-2n_{2}^{2})=0}$ ${\displaystyle n_{2}^{2}={\tfrac {1}{2}}}$ ${\displaystyle n_{1}^{2}+n_{3}^{2}={\tfrac {1}{2}}}$

${\displaystyle {\begin{aligned}\sigma =&\sigma _{1}n_{1}^{2}+\sigma _{2}n_{2}^{2}+\sigma _{3}n_{3}^{2}={\frac {1}{2}}(\sigma _{1}+\sigma _{2})\\\tau ^{2}=&(\sigma _{1}-\sigma )^{2}n_{1}^{2}+(\sigma _{2}-\sigma )^{2}n_{2}^{2}+(\sigma _{3}-\sigma )^{2}n_{3}^{2}=\left({\frac {\sigma _{1}-\sigma _{2}}{2}}\right)^{2}=\left({\frac {\sigma _{3}-\sigma _{2}}{2}}\right)^{2}=\tau _{1,3}^{2}\end{aligned}}}$

and the main shear stress is on a circular ring, the red ring in the picture.

Thus, in each of the three cases (1), (2) and (3), either one of the formulas given at the beginning for the main shear stress or the shear stress disappears as a minimum in the main stress directions or in the hydrostatic stress state.

Derivation with the help of tensor calculus

A calculation of the main shear stresses with the help of the tensor calculation can be found with the stress tensor .

example

Amount of the shear stress in the tangential planes of a sphere with the principal stresses σ ₁ = 4, σ ₂ = 0 and σ ₃ = -2

A stress state is considered with the principal stresses σ ₁ = 4, σ ₂ = 0 and σ ₃ = -2 (the units are suppressed for the sake of clarity). Then the main shear stresses are calculated

${\displaystyle {\begin{aligned}\tau _{1}=&{\frac {|\sigma _{2}-\sigma _{3}|}{2}}={\frac {|0-(-2)|}{2}}=1\\\tau _{2}=&{\frac {|\sigma _{3}-\sigma _{1}|}{2}}={\frac {|-2-4|}{2}}=3\\\tau _{3}=&{\frac {|\sigma _{1}-\sigma _{2}|}{2}}={\frac {4-0}{2}}=2\end{aligned}}}$

The figure shows the amount of shear stress in the tangential plane at a point on the surface of the sphere, color-coded from blue (0) to red (3). The main shear stresses are present in the three points shown in bold black and the shear stress is stationary . The point in the red area marks the global maximum, i.e. the maximum shear stress, and the other two points lie in saddle points . The shear stresses disappear in the main stress directions (blue areas). Here the shear stress is in the global minimum.

literature

• Ralf Greve: Continuum Mechanics. A basic course for engineers and physicists . Springer, Berlin et al. 2003, ISBN 3-540-00760-1 .
• Hans Albert Richard, Manuela Sander: Fatigue cracks. Recognize - judge reliably - avoid, 2nd edition, Springer Fachmedien, Wiesbaden 2012, ISBN 978-3-8348-1594-1 .
• Hans Albert Richard, Manuela Sander: Technical Mechanics. Strength theory, textbook with practical examples, 2nd edition, Vieweg + Teubner Fachverlag, Wiesbaden 2006, ISBN 978-3-8348-0454-9 .

Web links

• Superposition of stresses, principal normal stresses, flow hypothesis (accessed on September 20, 2018)
• Stresses and transmission capacity of the weakened shaft-hub-press connections (accessed on September 20, 2018)
• Analysis of the manufacturing and process influences on the formation of stress cracks when joining amorphous thermoplastics using a heating element (accessed on September 20, 2018)
• Corrosion-resistant rolling bearings in hydraulic fluids containing water (accessed on September 20, 2018)
• Meaning of the calculated stress and deformation values (accessed on September 20, 2018)