Material model
A material model , material or material law , is a quantification of physical material properties. Material properties determine the ability of a material to react to physical influences (such as forces, heat input or currents). Material models are independent of the shape of a body and are mostly experimentally motivated. The aim of a material model is to be able to predict how and to what extent the material will react to external influences. As models, they mathematically map relevant relationships for the model creator, i.e. they are mathematical models that have an originator, the model creator. Even if they are often referred to as material laws, they do not have the general validity of physical laws, because different models from different modelers can exist for the same material, which differ in the area of application, the dependencies considered, the calculation effort, the accuracy and their range of validity.
The reactions of a material are called material quantities and the influencing quantities are called constitutive variables . The connection of the constitutive variables and material quantities is done in equations called material or constitutive equations . Furthermore, inequalities can also occur which separate the different behavior modes (such as plastic flow, phase transitions) of the material from one another. The simplest conceivable relationship between material size and constitutive variable is proportionality: The material size is equal to a constitutive variable multiplied by a constant. Such a relationship often has a defining character for a material property, as the examples specific heat capacity , permittivity , permeability (magnetism) on the page material constant show. Material properties and therefore also the material constants are always dependent on the temperature, which can be taken into account with temperature coefficients . If further or more complex dependencies are considered relevant in the analysis case under consideration, the model creator steps in, who then creates a model suitable for the case under consideration (if one does not already exist). The development from the first definition of a property and quantification with a material constant through the consideration of a temperature dependence to complex models is traced. The reasons for the complexity can be non-linearities, multiaxiality or dependence on several constitutive variables.
The continuum mechanics has its own field of knowledge, the material theory , which deals with the classification of materials and material properties and the creation of media models. The materials science developed material models from the need to characterize precisely as possible of their developed materials.
Scope
Material models have a limited validity because they do not take into account influences excluded by the model creator. When applying the models, it is important to ensure that the assumptions on which the model is based apply, such as:
- Ambient conditions such as temperature or pressure
- Time spans over which the material behavior is to be observed (long-term or short-term behavior).
- Rates of change of the constitutive variables. A distinction is made between static, quasi-static, moderate rates and high-speed ranges.
- Size scale of the material samples. A distinction is made between macro, meso or micro level of observation.
- Chemical condition. Materials can change their properties through corrosion .
Physical framework
On the one hand, materials are subject to the laws of physics such as conservation of mass, momentum and energy or Maxwell's equations. On the other hand, a material sample follows geometric bonds, which are the specialty of kinematics and which describe the possible movements and resulting deformations and strains. Material models that indicate a quantitative relationship between the variables in these physical and kinematic equations are suitable for calculating the reactions of a body that follows the laws of nature to external influences.
The second law of thermodynamics has a special status: When setting up material models, care must be taken that the entropy production of the material is not negative for all possible temporal courses of the constitutive variables.
Simple materials
Some material properties are so complex that they can be illustrated using the reaction of test objects as an example. Examples of this are impact strength , notched impact strength or component Wöhler lines . It is more about component properties, because the separation of material properties and sample properties (shape, size or surface properties of the test specimen) is not reliable or not possible with justifiable effort. For most material properties, however, the notion that any part of a material sample has the same properties as the sample itself has worked well. To determine the material response at a point on the sample, one then only needs to consider an (infinitesimal) small area around the point. The material reacts locally to local influences. Experience also shows that the material response depends entirely on past or present influences, but not on future influences, that is, materials are deterministic . The principle of material objectivity states that an observer who moves in any translotoric or rotational manner measures the same material response as an experimenter who is at rest relative to the sample. Materials that are local, deterministic and objective are called simple and only these are the subject of classical material theory .
Material equations
Objective sizes
Only objective quantities can be used for material quantities and constitutive variables, i.e. H. those that an observer who moves in any translator or rotation perceives in the same way as an experimenter who is at rest relative to the sample. Mass, density, temperature, heat, specific internal energy and entropy are scalar objective quantities. Objective directed quantities, vectors, are e.g. B. Forces, stress, heat flow and entropy flow vectors. The speed of a particle is z. B. not an objective variable, because it is judged differently by differently moving observers. Furthermore, in some natural laws, tensorial quantities occur, the objectivity of which must be checked in each individual case. Cauchy's stress tensor , which is an objective quantity, should be mentioned here as an important example .
Types of material equations
Equations that describe a material can be divided into three classes:
- Those that indicate the material symmetry or direction dependence. In this case, the properties of the material are different in one direction than in the other. A well-known example of this is wood, which behaves differently in the direction of the grain than across it.
- Material constraints prohibit certain changes to a material. The best known example of this is incompressibility, in which the volume of a material sample cannot be changed.
- Constitutive equations that formulate the functional relationship between material sizes and the constitutive variables.
While the members of the first two classes are algebraic in nature, the constitutive equations can have other forms:
- Differential equations,
- Integral equations,
- algebraic equations and
- Inequalities,
see the example below.
Conservative materials
Conservative materials have a special form of constitutive equations in which the material size results from the derivation of a scalar potential according to the constitutive variable. An example of this is Hooke's law where the potential is the deformation energy. Here you have the special properties:
- Path independence : The material size always has the same value for a given value of the constitutive variable, regardless of the path on which the final state was reached.
- Conservativity : If the potential is an energy, no work is done or energy is consumed along a closed path. Work that has been expended is fully returned by the system until you return to the starting point.
Material parameters
For the quantification of the material behavior, the constitutive equations contain material parameters or - as they are also called - material constants that allow the model to be adapted to measured values. It is common practice to design the model so that the parameters have positive values for real materials. If negative values occur during the adjustment, caution is usually required.
Mechanical solid models
The following list shows representatives of the four material models of classical continuum mechanics for solids.
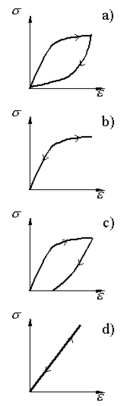
- If the stress-strain curve is identical for loading and unloading, the material law is elastic or ideally elastic ( b or d in the picture) and not viscous, i.e. H. speed independent. Ideally elastic material laws do not necessarily have to be linear, but can also be non-linear ( b in the picture). If a material law is linear and ideally elastic ( d in the figure), one speaks of a linear, ideally elastic law . Since this expression is very long, it is abbreviated to a linear law of elasticity or simply a law of elasticity , e.g. B. Hooke's law .
- If the stress-strain curve arrives at the starting point again during relief, but if the path during relief differs from that during stress ( a in the picture), the material law is viscoelastic and you can see a hysteresis . In the case of very slow stress-strain curves, the hysteresis disappears and you can see a curve as in Figure b . Rubber-like substances show such behavior.
- If the start and end point are not the same, one speaks of a plastic material law ( c in the picture). This applies to substances that flow during exposure, see also the example below. Here one observes a hysteresis that is independent of the rate of expansion.
- If the start and end point are not the same and a hysteresis that is dependent on the strain rate is observed, but which does not disappear even with very slow stress-strain curves, there is viscoplasticity. The hysteresis curve for very slow stress-strain processes is called equilibrium hysteresis here .
The four named material classes are therefore dependent or independent of the expansion rate and show an equilibrium hysteresis or not. The creep is a property of viscous substances.
If there is a linear relationship between stress and strain, one speaks of a linear material law ( d in the figure). It must also be linear with regard to its temperature expansion. Laws that do not show a linear relationship are called nonlinear material laws .
example
The ideal plasticity should serve as an example, the material equations of which contain both algebraic and differential equations and a case distinction. With ideal plasticity, there is no solidification during plastic flow, ie the stress-strain curve has a horizontal course during flow. Dough is roughly ideally plastic. In practice, this model is used when only the yield point is known and one does not want to overestimate it when calculating the stiffness of a component.
In the important special case of uniaxial tension / compression, one can restrict oneself to scalar quantities and simplify the material equations very much. The way there is taken as in a multi-axis plasticity model with several constitutive variables. The constitutive variable is the total strain and the material size is the stress . The tension is positive in the tensile area and negative in the pressure area. The material has an elastic area in which the material reacts elastically and a plastic area where plastic flow takes place. The flow is represented by the plastic strain , which is an internal variable of the model. The plastic strain cannot be influenced or specified directly from the outside. The difference between the total elongation and the plastic elongation is the elastic elongation. The total strain is divided into an elastic and a plastic part:
where is the elastic portion. The tension depends on the elastic elongation via a law of elasticity:
where the material parameter is called the modulus of elasticity . The plastic strain only develops when the stress reaches the yield point , which is another material parameter. The flow function shows the distinction between elastic and plastic areas:
- .
Is in the elastic range . With plastic flow, and therefore , is what the special characteristic of ideal plasticity is. However, it can also apply with constant elongation, which is why flow only occurs when is. The yield criterion is therefore
- and .
An associative flow rule determines the evolution of the plastic strain in the case of plastic flow:
- .
This is the plastic multiplier , which is derived from the consistency condition :
with plastic flow. For the evolution of plastic strain, this means:
- .
The reverse is true in the elastic range , that is .
The material equations of ideal plasticity can thus be summarized in the uniaxial case as follows:
| Flow function | |
|---|---|
| Stress-strain relationship |
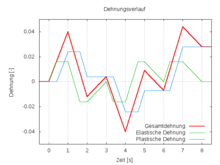
The images on the right show diagrams of a simulated strain-controlled tensile test. The upper picture shows the course of the strains, the middle one shows the course of the stress over time and the lower picture shows the stress-strain diagram of this ideally plastic material. The material parameters used were:
| parameter | ||
|---|---|---|
| value | 10,000 | 160 |
| unit | MPa | MPa |
At the end of the test, after eight seconds, the sample was relieved after a total elongation of 0.045, so that the tension disappears, and therefore also applies. In the end, however, one observes remaining strains that correspond to the plastic strains. Your size is
- .
A real body made of this material would not return to its original state at the end of the experiment, which is the characteristic of plasticity.
See also
Thermodynamics:
Fluids (liquids or gases):
Solid:
Fabric properties:
- Substance property
- Material properties
- Material databases provide information on many materials.
- Materials science and technology develops and characterizes materials.
literature
- H. Altenbach: Continuum Mechanics . Springer 2012, ISBN 978-3-642-24118-5 .
- Ralf Greve: Continuum Mechanics. Springer, 2003, ISBN 3-540-00760-1 .