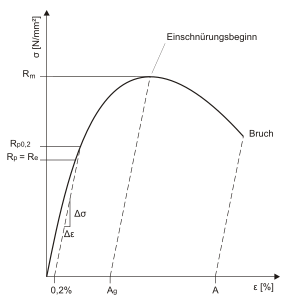
Stress-strain diagram

In technology it is often of great importance to exactly know the properties of a material used in terms of its strength , its plasticity or its brittleness , its elasticity and some other properties.

For this purpose samples of material are in the tensile test tested by the sample of known initial cross-section in a tensile testing machine clamped and a tensile force F is loaded.

When the force is increased, it is then graphically displayed against the change in length ΔL caused . This curve is known as the force-elongation diagram .

In order to obtain a measurement curve that only depends on the type and structure of the tested material, i.e. not on the geometric dimensions of the sample, reduced units are used, i.e. the change in length ΔL is based on the initial length L ₀ and the force F on the vertical Cross-section S _{0 of} the body in the undeformed state.

This curve, which is now independent of the specimen shape, is called the stress-strain diagram .

Elongation :

${\displaystyle \varepsilon ={\frac {\Delta L}{L_{0}}}}$

(Nominal) voltage :

${\displaystyle \sigma ={\frac {F}{S_{0}}}}$

The strain is a magnitude of the number of dimensions . It is often given in percent or in alcoholic beverages (e.g. "0.3% yield point").
The unit of tension is N / m² (= 1 Pa). In mechanical engineering and materials science, the unit 1 N / mm² (= 1 MPa) is often used.

Depending on whether the experiment is carried out with tension control or expansion control, the tension or the expansion is the independent variable. However, it has become common practice to always apply tension over the stretch.

The (technical) voltage always relates to the output cross-section . However, the true stress continues to increase in the tensile test from as the cross-sectional area is reduced due to constriction. However, the true stress cannot be determined directly with the tensile test , so the technical stress is almost always used . One possibility to determine the true voltage is the simultaneous optical evaluation. ${\displaystyle S_{0}}$ ${\displaystyle R_{\mathrm {m} }}$ ${\displaystyle \sigma }$

There are different areas in the stress-strain diagram:

• the linear-elastic range (proportional range, "Hooke's straight line"), in which the strain is proportional to the tension and thus Hooke's law applies
• the non-linear elastic range in which the deformation is still reversible (elastic) but is no longer proportional to the stress.
• the elastic-plastic area , in which the deformation is partially plastic - that is, irreversible. If the elastic limit is exceeded, permanent deformations arise in the component due to dislocation movements that are temperature and strain rate dependent (thermally activated flow).

Structural steels show a pronounced yield point effect , which is caused by interstitially embedded foreign atoms such as carbon and nitrogen.

• 

  Fig. 1 Schematic stress / strain diagram with pronounced yield strength

• 

  Fig. 2 Schematic stress / strain diagram with continuous start of flow and entered 0.2% yield strength

• 

  Fig. 3 Schematic fine expansion diagram

The following abbreviations have been used in the diagrams:

• ${\displaystyle R_{\mathrm {m} }}$= Tensile strength
• ${\displaystyle R_{\mathrm {eH} }}$= upper yield point
• ${\displaystyle R_{\mathrm {eL} }}$ = lower yield point
• ${\displaystyle R_{\mathrm {p0,2} }}$= Yield strength with 0.2% plastic deformation
• ${\displaystyle E}$= Modulus of elasticity
• ${\displaystyle A}$= Elongation at break
• ${\displaystyle A_{\mathrm {g} }}$= Uniform expansion
• ${\displaystyle A_{\mathrm {L} }}$= Lüders expansion

See also

• Material testing

literature

• Eckard Macherauch: Internship in materials science. 10., verb. Ed., Vieweg, Braunschweig 1992, ISBN 3-528-93306-2