Profile (fluid dynamics)

In fluid mechanics, a profile is the shape of the cross-section of a body in the direction of flow. The flow around a liquid or a gas causes forces acting on this body .
Specially shaped profiles are particularly suitable for generating dynamic lift with little flow resistance . Examples of this are the profile of bird wings, wings on aircraft, hydrofoils , propellers on ships or turbine blades . Since the shape of the profile has a great influence on the forces on the body in flow, the development and characterization of profiles is an important part of aerodynamics .
Significance of the flow around the profile for aerodynamics
Determining the aerodynamic properties of an aircraft is a great challenge, both theoretically and experimentally. Therefore, attempts were made early on to determine the aerodynamic properties of the entire aircraft from the properties of its parts (e.g. wings, fuselage and tail unit). The aerodynamic properties of a wing can, under certain conditions, be divided into the properties of the profile sections around which the air flows and the properties of the wing outline itself. The conditions here are the absence of larger 3-D effects in the individual profile sections, which is the case with wings with a high degree of elongation and low taper and sweep (see gliders ). The two-dimensional flow around a profile then represents a great simplification (in theory as well as in experiment) compared to the flow around a three-dimensional aircraft (or wing) and allows z. B. carry out extensive parameter studies, which would not be possible for 3-D configurations.
Geometric categories
Profiles can be divided into different categories based on geometric or aerodynamic properties.
Profile types
- Symmetrical profilesare mirror-symmetrical along their longitudinal axis. The skeleton line is straight. Such profiles are used where there is a need to generate buoyancy or downforce, e.g. B. tail units on airplanes or rudders on ships.
- Semi-symmetrical profiles have no symmetry. It has become common practice to use this designation to classify profiles that have a curvature, but no concave contours. Such profiles are used when a low lift value is desired, for example in aerobatics.
- Profiles with a flat bottom have advantages in terms of mechanical construction. The best-known profile in this category is the Clark-Y with 11.7% thickness and 3.5% curvature.
- Normal profiles are convex at the top and S-shaped at the bottom. The concave lower and rear area is also called a hollow arch.
- Club profiles are similar to normal profiles , but have a distinctly low reserve thickness for good properties in the critical Reynolds number range .
- S-impact profiles : The rear part of the profile is drawn upwards so that the skeleton line at the profile exit is directed slightly upwards. However, this does not mean that an S-impact profile must be externally recognizable. So z. For example, the NACA-230 profile series has an almost straight line on the top in the rear area, while the bottom is convex. This can also be seen in the rotor blade of the Kamow Ka-26 shown opposite. S-flapping profiles have a very low negative, a neutral or even a positive torque coefficient Cm0. Special forms are the so-called supercritical or transonic profiles, which practically represent an S-shaped profile lying on its back.
Geometric parameters
- Profile depth (t = 1) is now the longest line from the profile nose to the profile rear edge and is also identical to the profile chord and the x-coordinate. In the past, the lower support line of the profile was defined as a chord or as a reference line for the wing chord or coordinate axis for the profile contour.
- Profile curvature (f / t) is the name given to the greatest deviation of the skeleton line from the profile chord. With S-impact profiles it is the difference between the front and rear deviation. Together with the reserve, it determines the torque at the neutral point and thus the pressure point migration. A large curvature enables a high coefficient of lift.
- Cavity (h / t) is the greatest deviation of a profile bitangent from the profile contour. It is usually only located on the lower side of the profile at the rear and has a major influence on the top speed of aircraft. Not all profiles have a concavity. Only a few S-shaped profiles have a hollow arch on the top.
- Profile thickness (d / t) is the largest possible circle diameter on the skeleton line. The thickness and its back position, together with the curvature, also determine the maximum lift. Thin profiles with a pointed nose are only suitable in the sub-critical speed range.
- Nose radius (r / t) denotes the radius of the nose circle of the profile nose . Large nose radius usually means little thickness reserve.
- Rear edge angle (τ) is the angle at the rear edge between the top and bottom of the profile.
- Arch reserve (xf / t) denotes the distance from the profile nose that the point has at the maximum height of the skeleton line. It is usually located behind the thickness reserve and largely determines the moment coefficient and thus the pressure point migration.
- Thickness reserve (xd / t) denotes the distance of the greatest thickness above the profile chord from the profile nose. It is usually located in front of the arching reserve. Thin profiles with a large nose radius always have a small thickness reserve.
Aerodynamic categories
- Low Re profiles are used primarily with model aircraft used and very slowly flying gliders. They are characterized by a larger concavity. The greatest thickness of the rather thin profiles is on the anterior quarter of the tendon.
- Conventional profiles are mainly used in the speed range of small aircraft. They have a straight or slightly convex shape on the underside of the profile and the greatest profile thickness is in the front third of the wing depth.
- Laminar profiles have a long laminar flow path and therefore a low resistance. The thickest part of the profile is just in front of the center of the wing and the nose radius is rather small. Such profiles react more sensitively to disturbances in the flow, which arise among other things from roughness and pollution of the surface, and are mainly used in gliders and light powered aircraft.
- Transonic profiles (supercritical profiles) show a lower or weaker increase and decrease in flow velocity on the upper side. The air flows there from the subsonic into the transonic and back into the subsonic area. The shock wave recompression turns out weaker and remains the collision-induced detachment. Such profiles were primarily made possible by CFD and are used in aviation in almost all commercial aircraft in the near-sound speed range.
- Supersonic profiles : are made as thin as possible, have practically no curvature and have pointed profile noses.
Types of flow
Influence of the Reynolds number
The most important key figure for the flow around the profile is the Reynolds number . It determines the influence of friction (viscosity) on the flow. With the flow around the profile, the Reynolds number is formed with the flow velocity and the profile depth. The Reynolds number falls below a certain (profile-dependent) value (Re crit ) it is called subcritical, otherwise of supercritical flow around.
Sub-critical flow around the profile
The small Reynolds numbers of the subcritical flow around the profile express the dominant influence of the viscosity. The boundary layer is comparatively thick and laminar over long distances. An increase in pressure in the direction of flow leads to laminar separation of the boundary layer even at moderate angles of attack. Due to the separation, the profile experiences a relatively high flow resistance and generates little lift.
Supercritical flow around the profile
If the flow is applied to the profile with a supercritical Reynolds number, the profile performance improves dramatically. Due to the higher Reynolds number, the transition from the laminar to the turbulent boundary layer takes place either without separation or within a laminar separation bubble. In any case, the boundary layer is mostly adjacent. Practically all technically used profiles are operated supercritically.
Influencing the critical Reynolds number
Due to the poor profile performance with a subcritical flow, a supercritical flow is to be aimed for in any case. For this, the critical Reynolds number of the profile must be smaller than the Reynolds number. Particular attention must be paid to this fact, especially in applications with small Reynolds numbers, such as B. model airplanes. If the Reynolds number is around 500,000 or greater, then supercritical flow is automatically guaranteed for the commonly used aerospace profiles.
Some design guidelines for profiles with a small critical Reynolds number
In the lower critical Reynolds area, only moderate profile thicknesses and high profile arches are attached. Thin profiles have lower overspeeds and therefore a smaller pressure increase. The resulting small nose radius ensures the formation of a suction tip on the profile nose and the early transition of the boundary layer into the turbulent state. The turbulent boundary layer can then better cope with the pressure increase in the rear profile area. The installation of suitable turbulators on the profile also ensures that the boundary layer changes in good time. Alternatively, turbulence can also be generated by a wire stretched in the direction of the span in front of the profile nose. In the lower transition area, the following profile thicknesses are optimal for good glide and sink rates: Re 1000 4%, Re 50,000 6%, Re 100,000 8%, Re 500,000 12%. In the subcritical area, there are high arched thin profiles with a pointed leading edge (hall flight models ).
Mach number influence
The second important figure for the flow around the profile is the Mach number , which indicates the influence of compressibility on the flow around the profile. Depending on the inflow number Ma inf , the following flow ranges can be distinguished:
Incompressible flow around
(typical: Ma inf <0.3) The flow can be regarded as incompressible . The only relevant parameter for the flow is the Reynolds number.
Subsonic flow around
(typically: 0.3 <Ma inf <0.7) The flow has subsonic speed in the entire field. There are therefore no compression shocks and expansion fans and no wave resistance. The influence of the compressibility of the air can be very easily z. B. can be recorded with the help of the Prandtl-Glauert rule and only plays a subordinate role in profile design. The upper limit is only to be understood as a rule of thumb. For high-lift configurations, supersonic areas can arise even with much lower inflow numbers.
Near sound / transonic flow
(typical: 0.7 <Ma inf <1.2) In transonic currents, both subsonic and supersonic regions occur. If the flow is subsonic, supersonic areas are formed around the profile, which are usually closed off by shock waves. If the flow is supersonic, a raised head wave with a subsonic area forms in the nose area. This Mach number range is the most difficult to determine mathematically and the place of use of numerically optimized supercritical profiles.
Pure supersonic flow
(typically: 1.2 <Ma inf ) In the entire flow field the air has supersonic speed. Disturbances only propagate downstream (in the so-called Mach cone). Typical profiles for this purpose are very thin, not arched and have a pointed front edge.
Aerodynamic parameters
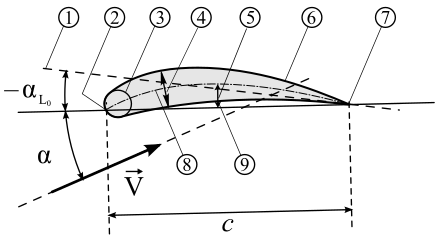
The air forces that occur on a profile can be reduced to a force acting on the pressure point . This force (R) can be divided into dynamic lift (A) and drag (W). The flow resistance points in the direction of flow and the dynamic lift is perpendicular to it. They are shown, possibly together with the torque, in the polar diagram . The torque (M) around the wing axis, but also lift and drag can be plotted against the angle of attack (α) in the resolved polar diagram .
Instead of these forces and moments, the dimensionless coefficients , and are used . This means that all forces are related to the dynamic pressure and the wing area (not to the frontal area, which is dependent on the angle of attack, across the direction of flow), the moments are also related to the profile depth, and you can calculate with values that are independent of the airspeed, the air density and the size of the Wings are. and , depending on the direction of force, can assume positive and negative values in relation to the profile.
- is the coefficient of lift. Its value is proportional to the angle of attack over a wide range. A positive value corresponds to lift, a negative value to downforce.
- is the coefficient of air resistance in the direction of flow. Its value changes little in the normal operating range and is always positive.
- is the coefficient of the torque at the t / 4 point of the chord. Its value depends only slightly on the angle of attack in the operating range of most profiles.
- is the calculated coefficient of the torque at the neutral point. The definition of the neutral point makes it independent of the angle of attack. That is why it is usually listed as a single value and not as a measurement curve like .
- is the distance between the neutral point and the leading edge of the profile in relation to the profile depth. For supercritical profiles it is between 25% and 28% of the depth.
It should be noted that all profile polars are calculated on infinite extension. The lift value of a real (finite) wing and above all the drag value must be corrected according to the aspect ratio (see lift coefficient and induced air resistance ).
Important points on the polar of profiles
- E opt is the best glide ratio . It is the largest possible ratio of forward speed to descent speed or Ca to Cw on the polar diagram. The associated Ca value is always in the upper buoyancy range.
- E sink_min is the glide ratio for the smallest sink. The associated Ca value is slightly above Ca opt .
- α0 is the zero lift angle , the angle of attack at which the lift disappears. It is always negative for lift profiles, 0 ° for symmetrical profiles and it can be 0 ° or even positive for S-flapping profiles.
- Cm0 is the coefficient of zero lift torque . This torque occurs with all asymmetrical profile shapes and is usually less than the calculated Cm and the Cm25 measured in the normal range. The direction of rotation is denoted as negative (-) when the profile nose is pressed down. It can be measured at the neutral point or at the t / 4 point or anywhere on the profile chord.
- Ca0 is the zero-angle lift, the lift at zero angle of attack. In the vicinity of this point the resistance becomes minimal. It is also proportional to the neutral torque.
- Cw0 is the coefficient of zero lift drag , the drag without lift. The theoretical maximum speed of an aircraft is at this operating point.
- Ca max is the maximum lift coefficient. It depends on the nose radius, curvature and thickness. It determines the minimum speed in level flight.
- Ca opt is the coefficient of lift during the best glide. Its value can be up to half below Ca max or even below (~ Ca 0.35 -Ca0.5)
- Ca sink_min is the buoyancy at the slightest sink . Its value is between Ca opt and Ca max or more precisely at (Ca 1.5 / Cw) max .
- Ca travel is the coefficient of lift at the best ratio of horizontal distance to time. Its value is between Cw min and Ca opt at about (Ca 0.5 / Cw) max .
- Cw min is the least resistance. It is usually located at zero angle of attack, that is, when the flow is in the direction of the chord (see also Ca0). This point on the polar usually corresponds to the cruising speed.
- α crit is the angle of attack at which the flow breaks off and many aerodynamic laws no longer apply. It is usually a little above the angle for maximum lift.
Geometric and aerodynamic relationships
Curvature and thickness are important geometrical profile sizes. Together they determine the maximum lift. The curvature and its reserve are important for the moment coefficient. These geometrical variables determine the shape and the position of the profile polar. In many catalogs with profile numbers , the first number means a code for the bulge, the second number a code for the bulge reserve, and the third number a code for the thickness. The thickness reserve is closely related to the thickness itself.
An important aerodynamic profile size is the glide ratio. The maximum glide ratio (best glide) is also called "efficiency". Small sink and fast flying are also important. The smallest sink rate is at slightly higher lift values (lower speeds), the "cruise" at slightly lower lift values (higher speeds) than that of the best gliding. Good performance values are achieved with a curvature plus thickness of 17%. The nose radius or the thickness and its back position have a major influence on the angle of attack range (lift range from Cw min to Ca max ). High-speed profiles have little curvature and a smaller thickness. The largest possible ratio of maximum to minimum speed can practically only be achieved with variable curvature ( flaps ).
- The increase in lift depends linearly on the angle of attack in the normal range of application. The slope ΔCa / Δα is about 0.11 Ca per degree for all profile shapes.
- The maximum lift is determined by the curvature , the thickness and its back position .
- The neutral torque , the zero lift angle and the zero angle lift are determined by the curvature and its backward position .
The following relationship applies to normal profiles: Cm = f · xf · -6; α0 = Cm x 40 °; Ca0 = α0 * 0.11. Ca max is strongly dependent on the Re number. The geometric profile curvature f depends on the definition of the profile chord. The value of Cm0 can be less than half of Cm if the flow type in the normal operating range is not the same as at zero lift. The following example shows in principle the connection between the geometric profile data - thickness and thickness reserve, curvature and curvature reserve - with the aerodynamic key values of wing profiles.
Basics
A profile has the following designations and geometric and aerodynamic characteristics:
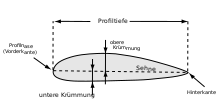
- Profile nose (English leading edge ) - the leading edge (VK or profile leading edge or wing leading edge ) of the profile (note: in the following text only the term leading edge is used);
- Trailing edge (engl. Trailing edge ) - trailing edge (HK) of the profile;
- Rear edge angle - among other things because of the manufacture and durability of the profile, the rear edge must not be too pointed; the rear edge must therefore have a certain radius of curvature;
-
Profile depth (t) (engl. Chord length ) - the distance between the front and rear edge of the profile (identical to the chord). When calculating the profile, the profile depth is used as a reference value. The profile depth is set equal to 100% (or equal to 1.0). Example:
- 20% thickness reserve for a profile with a profile depth of 1.90 m (calculation: x = 20 · 1.90 / 100 = 0.38 m) is 0.38 m (measured from the front edge).
- A profile thickness of 12% for a profile with a profile depth of 1.90 m (calculation: x = 12 * 1.90 / 100 = 0.228 m) is 0.228 m.
- Chord (s) (engl. Chord ) - the straight line connecting leading and trailing edges of the profile. The profile contour is specified in the xy coordinate system, with the origin at the front edge at the level of the chord and the x-axis being identical to the chord. At the trailing edge of the profile at the level of the chord, x = 1.0 or x = 100%. The length of the chord (the profile depth) x = 1.0 is the basic dimension to which all other dimensions are given as a ratio . On the profile chord y = 0.
- Skeleton line (engl. Camber ) - the center line of the profile which connects the center points of all circles that fit into the profile, that the curve everywhere to the top and bottom of the same profile (transverse) distance has. Most of the profile properties such as B. Cm0 or the later area of application can already be derived from the shape of the skeleton line, even before a suitable symmetrical profile drop is adapted to this. With the classic asymmetrical profiles, the skeleton line lies completely above the profile chord, with S-profile profiles it touches or intersects the profile chord in the rear area of the profile. The skeleton line can be determined from the y-values of the profile top (y o ) and the profile bottom (y u ), it is identical to the y-values of the relative curvature: f '= y o - (y o + y u ) / 2.
-
Profile curvature (f) (English camber ) (curvature of the profile) and maximum profile curvature (English camber ) (f max )
- maximum profile curvature - the maximum distance between the profile chord and the skeleton line; the distance between the skeleton line and profile chord at the maximum of the curved skeleton line;
- Profile curvature - the distance between the profile chord and the skeleton line;
- The profile curvature can be determined from the y-values of the profile top (y o ) and the profile bottom (y u ): f = y o - (y o + y u ) / 2 (distance of the chord from the top minus distance of the skeleton line from the top). The largest value for f is f max .
- Symmetrical profiles do not have a curved skeleton line - their profile curvature is zero.
- Arch reserve (x f ) - the distance of the maximum profile arch from the leading edge; relative arch reserve (x ' f = x f / t);
- Profile thickness (d) and maximum profile thickness d max - this usually means the maximum profile thickness, the maximum distance between the top and bottom of the profile;
- Thickness reserve (x d / t) - the distance of the maximum profile thickness from the leading edge (in relation to the profile depth); relative thickness reserve (x ' d = x d / t);
- Thickness Ratio (or: Relative Profile Thickness or Relative Thickness Ratio) - the maximum profile thickness in relation to the profile depth; Profile thickness / profile depth (δ = d / t);
- Nose radius (engl. Leading edge radius ) (r N ) - the radius of the nose circle at the leading edge; Nose radius in relation to the tread depth (r N / t). However, especially with regard to today's inverse calculation methods (spline interpolation with coordinate points that are very close to one another), it is not absolutely necessary for a geometrically correct circle to appear on the profile nose at all.
- Camber ratio: profile camber / profile depth (f '= f / t);
- Pressure point ;
- Position of the neutral point ;
- Drag coefficient (c W );
- Lift coefficient (c L );
- Moment coefficient (c M ) (pitching moment coefficient);
- Torque (profile) .
- Zero buoyancy .
The symbols for the individual geometric parameters of a profile are handled very inconsistently from textbook to textbook. As an example, only some of the symbols used in Germany are listed here:
- Nose radius: r or r N or a.
- maximum profile curvature: f or p.
- Profile depth: t or l 0
- Arch reserve: x f or m;
- Thickness reserve: x d / t or b.
Have the greatest influence on the properties of the profile:
- Profile curvature,
- Arch reserve,
- maximum profile thickness,
- the change in profile thickness along the profile chord,
- Nose radius,
- Trailing edge (shape of the skeleton line near the trailing edge - straight skeleton line or curved upwards; angle between top and bottom at the trailing edge).
Development of profiles
Methods
In the early days of profile development, profiles were primarily developed based on their geometric parameters. Examples are the NACA profiles of the 4 series. A suitable symmetrical drop from the profile catalog is placed over a skeleton line from which certain properties are expected.
With the development of inverse design methods from the middle of the last century, it was possible to go over to directly stipulating the aerodynamically decisive pressure distribution and deriving the profile contour from it. These methods have been further developed to this day for incompressible (friction-prone) profile flow and are standard today (see XFOIL or the numerical Eppler code developed by Richard Eppler at the University of Stuttgart in the early 1980s ).
No such methods are known for the transonic (frictional) flow around the profile, and the profile contour must be determined by solving the compressible Navier-Stokes equations (or RANS equations) in conjunction with an optimizer.
Since the development and measurement of profiles is very complex, universities and other public institutions carried out systematic test series early on and published catalogs of proven profiles with known properties. The profile catalogs of the Aerodynamic Research Institute in Göttingen (Profile Gö-xxx) and that of the American NACA (National Advisory Committee for Aeronautics) (Profile NACA-xxxx) were widely used .
The system of the profile numbers of the NACA profiles corresponds to the chronological order in which they were created. The profiles of the four-digit and later the five-digit NACA series were intended for comparatively slow aircraft. While the later profiles of the six-digit, seven-digit and eight-digit NACA series were intended for high speeds in the subsonic range. The nomenclature of the NACA profiles made it possible to derive the exact profile geometry from the names of the profile.
Today, profile catalogs are rarely used for new developments, as the computing power and theoretical knowledge are available to numerically calculate new profiles tailored to the desired properties.
Criteria and boundary conditions
The flow conditions (i.e. the Reynolds and Mach numbers) in later operation are decisive for the selection or design of a profile. In the simplest case, only one operating point i is taken into account. A. but several, which then have to be weighted. Therefore, there cannot be the best profile, but only one best profile for a precisely defined application.
In almost all cases, the most important criterion is a high maximum glide ratio E max , i.e. H. the generation of lift with as little drag as possible. In addition, there are a number of other criteria:
- With the loss of E max , an attempt can be made to achieve a large E over a wide c a range (and thus speed range).
- A c a, max that is as large as possible defines (together with the wing loading) the later minimum speed of the aircraft. In the same way, the c a, min determines the minimum inverted speed or the ability to do so in general.
- The lowest air force c r, min determines the (aerodynamically possible) maximum speed in a dive.
- The pitching moment c m of the profile causes torsion of the wing or rotor blade and is important for stability and trimming of the flying wing .
- A good-natured tear - off behavior contributes to flight safety and relieves the pilot when flying in the border area. For aerobatic aircraft, on the other hand, a harder tear-off behavior is desired.
- Depending on the intended use, the profile must be suitable for the use of flaps or other oars.
Possible secondary conditions for the selection or the design of profiles:
- The height and cross-sectional area of the profile determine its static properties and the volume of the wing, which z. B. is important as tank volume.
- The achievable surface quality determines to what extent the aerodynamically possible laminar running routes on the profile can be used in practice.
- A covered wing can require the use of purely convex profiles. Profiles with a straight underside can also be found in the model area to minimize construction costs.
The different requirements often contradict each other (e.g. small c wmin and large c amax ). Really existing profiles are therefore always a compromise.
For example, the following properties are aimed for in gliders:
- maximum efficiency, d. H. maximum ratio of lift to drag, for a large maximum glide ratio
- flat speed polar, for good efficiency over a wide speed range
- high maximum lift at low speed, for good climbing in thermals and good landing properties
- Good-natured behavior at high angles of attack (tear-off behavior), for safe slow flight characteristics
- Tolerance to pollution (mosquitoes), rain.
Applications
The functional principle of the profile shape of a wing can be found in the wing of an aircraft, the rotor blade of a wind turbine, the drive propeller , the moving and guide blades of compressors and turbines, etc.
swell
- Klaus Engmann (Hrsg.): Technology of the airplane . 6th edition. Vogel, Würzburg 2013, ISBN 978-3-8343-3304-9 .
- Hermann Schlichting , Erich Truckenbrodt : Aerodynamics of the aircraft . 3. Edition. tape 1 . Springer, Berlin / Heidelberg / New York 2001, ISBN 3-540-67374-1 .
Web links
- Irrotational plane flows
- X-Foil , a program for calculating the properties of subsonic profiles
- xflr5 , a graphic program based on X-Foil
- Airfoil Investigation Database , an extensive collection of profile data with search function and calculated polars (in the Internet Archive )