pitch

The slope of a linear function corresponds to the quotient ${\displaystyle {\tfrac {\Delta y}{\Delta x}}}$

In mathematics , especially in analysis , the slope (also known as slope ) is a measure of the steepness of a straight line or a curve .

The problem of determining the gradient arises not only with geometric issues, but also, for example, in physics , in road construction or in economics . For example, the slope in a time-distance diagram corresponds to the speed or the slope in a time-charge diagram corresponds to the current intensity .

Slope of a straight line

Definition and calculation

Slope of a straight line

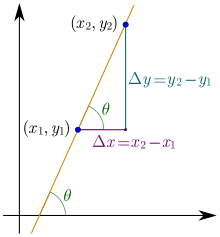
The slope of a straight line is often denoted by the letter . If Cartesian coordinates are used , the straight line defined by two points and has the slope ${\displaystyle m}$ ${\displaystyle (x_{1}|y_{1})}$ ${\displaystyle (x_{2}|y_{2})}$

${\displaystyle m={\frac {\Delta y}{\Delta x}}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}.}$

${\displaystyle \Delta x}$(read: Delta x) means the difference between the x values, corresponding to the difference between the assigned y values. ${\displaystyle \Delta y}$

For example, the slope through the points and results: ${\displaystyle (1|2)}$ ${\displaystyle (3|7)}$

${\displaystyle m={\frac {7-2}{3-1}}={\frac {5}{2}}=2{,}5}$

It does not matter from which points of the straight line the coordinates are used in the formula. For example , if you take and , you get: ${\displaystyle (-1|-3)}$ ${\displaystyle (1|2)}$

${\displaystyle m={\frac {2-(-3)}{1-(-1)}}={\frac {5}{2}}=2{,}5}$

If the straight line rises (in the positive x-direction, i.e. viewed from left to right), its slope is positive. For a falling straight line the slope is negative. Slope 0 means that the straight line runs horizontally, i.e. parallel to the x-axis.

If the straight line has the slope and it intersects the y-axis at the point , then it has the equation ${\displaystyle m}$ ${\displaystyle (0|c)}$ ${\displaystyle y=mx+c}$

Note: The straight lines parallel to the y-axis are not function graphs and therefore do not have a slope value . You can assign them the slope “infinite” (∞).

Road traffic

→ Main article : Gradient

The steepest street in the world with around 35% (19.3 °) is Baldwin Street in New Zealand.

Percentage gradient on a road sign (lower sign) in St Mawes , Cornwall

The gradient of a straight line also plays a role in road traffic . The traffic sign for the uphill or downhill gradient of a street is based on the same term for the gradient, but it is usually expressed as a percentage. A specification of 12% gradient means, for example, that the height increases by 12 m for every 100 m in the horizontal direction. According to the definition given above, one has to divide 12 m by 100 m, which leads to the result 0.12 (in percent notation 12%).

The steepest street in the world is Baldwin Street in New Zealand. The maximum gradient of the almost 350 meter long road is 1: 2.86 (19.3 ° or approx. 35%).

A ratio such as 1: 2.67 is another way of defining slopes or inclines. It gives, as well as a percentage, the difference in height per horizontal section : 1 m height over 2.67 m distance = 1 / 2.67 ≈ 0.37453 ≈ 37.45% (= 37.45 m height over 100 m distance ). Even banks are so stated. The often used ratio of artificial embankments of 1: 1.5 (depending on the material etc.) results in a height difference of 1 meter over a horizontal distance of 1.5 meters. That means a slope of 66.7% and a slope angle of arctan (1 / 1.5) = 33.7 °.

Incline or slope angle

With the help of the tangent and arctangent function, the gradient or inclination angle of the straight line can be calculated from the gradient of a straight line in relation to the positive axis: ${\displaystyle x}$

A connection from trigonometry says that in a right-angled triangle the tangent of one of the two acute angles is equal to the quotient of the respective opposite and adjacent cathetus, which makes it clear that the slope is also the tangent of the slope angle (in degrees) compared to the positive one -Axis is: ${\displaystyle x}$

${\displaystyle m=\tan(\alpha ).}$

When specifying in percent (%) it should be noted that the gradient and the gradient angle are not proportional to each other, so it is not possible to convert the gradient and gradient angle into one another with a simple rule of three . For example, slope 1 (= 100%) corresponds to a slope angle of 45 °, slope 2 (= 200%) on the other hand only corresponds to an angle of around 63.4 °, and for a slope angle of 90 °, the slope would have to be infinite to grow.

On the other hand, there is an approximate proportionality of the pitch and pitch angle only for small pitch angles up to about 5 ° - a pitch of ± 0.01 or ± 1% corresponds to a pitch angle of approximately ± 0.57 °, and vice versa a pitch angle of ± 1 ° a slope of approximately ± 0.0175 or 1.75%. Mathematically this can be explained by the fact that the derivative of the tangent in 0 is exactly 1, i.e. H. for values close to 0 applies . ${\displaystyle x}$ ${\displaystyle \tan(x)\approx x}$

For larger angles of inclination, on the other hand, or if their size is to be determined exactly, the inverse function of the tangent is required, i.e. the arctangent function :

${\displaystyle \alpha =\arctan(m).}$

In the example above one calculates:

${\displaystyle \alpha =\arctan(0{,}4)\approx 21{,}8^{\circ }.}$

In the case of negative gradients, it should be noted that - due to the point symmetry of the arctangent function - the gradient angles then also become negative. ${\displaystyle \alpha }$

Cutting angle

The term slope also provides a convenient method to determine the intersection angle of two straight lines with given slopes and : ${\displaystyle \varepsilon }$ ${\displaystyle m_{1}}$ ${\displaystyle m_{2}}$

${\displaystyle \tan \varepsilon =\left|{\frac {m_{2}-m_{1}}{1+m_{1}\cdot m_{2}}}\right|.}$

${\displaystyle \varepsilon =\arctan \left|{\frac {m_{2}-m_{1}}{1+m_{1}\cdot m_{2}}}\right|.}$

Two straight lines are parallel ( = 0 °) if and only if their slopes match. They are perpendicular to each other ( = 90 °) if and only if their slopes meet the orthogonality condition · = −1. ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon }$ ${\displaystyle m_{1}}$ ${\displaystyle m_{2}}$

Pitch of threads

In the case of metric threads , the pitch characterizes the pitch , i.e. the distance between two thread steps along the thread axis, in other words the axial path that is covered by one revolution of the thread.

In the case of imperial threads, on the other hand, the number of thread turns over the distance of one inch is specified as the value. The abbreviation TPI ("threads per inch") is often used as a pseudo unit .

Gradients in waters, in potential-driven processes and currents

In particular at hydropower plants , the local water level difference between the upstream and downstream water is referred to as the gradient (or working height). This applies to mills, run-of-river power stations, but also to constructions with tunnels, water locks and pressure pipes. The decrease in the water level between 2 distant points along a river is also referred to as a gradient.

In thermal power processes , for example on heat engines or refrigeration units, we speak of pressure and temperature gradients when there are discrete differences between the corresponding measured variables between 2 areas that lead to self-running flows of fluids (gas, liquid) or thermal energy.

Static pressure gradients can also exist between different points of supply systems for compressed air or tap water , as well as in ventilation systems (important for hygiene, clean rooms, odor nuisance). (A pressure drop occurs dynamically along a flow path.)

Chemical-physical processes are sometimes driven by a spatially existing material concentration gradient. Osmosis , diffusion , chromatography , crystallization from solution, evaporation are all mentioned here.

In a figurative sense, similarly in economics and sociology, differences in wage levels , price levels or education , e.g. regionally between town and country, socially between men and women, are referred to as wage gaps, price gaps, educational gaps.

In all of these cases, contrary to the usual term `` slope '' (as a negative slope), what is meant is not a slope in the sense of height difference per distance (length) and thus the unit of measurement 1, but a height difference (measured in the unit of measurement). All flow processes driven by this have in common (by themselves) only to run in one direction - downhill. (See potential difference .)

Generalization: slope of a curve

One of the fundamental problems of analysis is to find the slope of a curve at a given point on the curve. The formula discussed above can no longer be used since only one point is given. If you choose the second point arbitrarily, you will not get a clear result or, if both points are chosen identically, the result is not defined because it is divided by 0.

The slope of the graph of a function at a point on the graph is therefore defined as the slope of the curve tangent at this point. The differential calculation provides the concept of derivation as an aid to be able to calculate such slope values.

Example: For the graph of the function , the slope at the curve point and the associated angle of inclination are to be calculated. ${\displaystyle f:\;x\mapsto 2x^{2}-{\frac {1}{2}}x^{3}}$ ${\displaystyle (2|4)}$

First, one finds the equation of the derivative function : ${\displaystyle f'}$

${\displaystyle f'(x)=2\cdot 2x^{2-1}-{\frac {1}{2}}\cdot 3x^{3-1}=4x-{\frac {3}{2}}x^{2}}$

Now the x-coordinate of the given point is inserted:

${\displaystyle f'(2)=4\cdot 2-{\frac {3}{2}}\cdot 2^{2}=8-{\frac {3}{2}}\cdot 4=8-6=2}$

The angle of inclination results from the value of the slope:

${\displaystyle \tan \alpha =2}$

${\displaystyle \alpha =\arctan 2\approx 63{,}4^{\circ }}$

See also

• Rise , steepness

Web links

Wikibooks:: Mathematics for School ${\displaystyle {\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}}$

Wiktionary: slope  - explanations of meanings, word origins, synonyms, translations

• Website that automatically calculates derivatives and integrals
• Derivation using the example f (x) = x²

Individual evidence

1. ↑ Steven Morris: Welsh street loses world's steepest title after New Zealand rival's appeal. In: .theguardian.com . April 8, 2020, accessed on May 22, 2020.