Bernoulli's equation
The Bernoulli equation , also known as Bernoulli's law or (ambiguously) the Bernoulli theorem , is a statement about flows according to Bernoulli and Venturi . The theory about these essentially one-dimensional flows along a stream filament was created in the 18th century by Daniel Bernoulli and Giovanni Battista Venturi and forms the basis for important aero- and hydrodynamic calculations.
The Bernoulli equation states in the steady flow viscosity sfreier incompressible fluids (liquids and gases), that the specific energy of the fluid elements along a flow line is constant:
Here, u the velocity , p the operation pressure , ρ the density , g the gravitational acceleration and z the height above a reference plane in the gravitational field of the earth. The operating pressure is that portion of the static pressure that does not result from the fluid's own weight. The first summand represents the specific kinetic energy , the second the specific pressure energy and the third the specific positional energy . The specific total energy e constant on the streamline is determined by suitable reference values on the streamline and represents an integral of the movement along the streamline.
The multiplication of the equation with the (constant) density ρ gives the Bernoulli pressure equation
in which the total pressure is the sum of the dynamic pressure and the static pressure , which is composed of the operating pressure and the weight pressure of the fluid column . Division of the energy equation by the (constant) gravitational acceleration g yields a height equation that represents the original form given by Bernoulli:
In it, the sum of the velocity altitude , the pressure altitude and the geodetic altitude z (in the loss-free case) is constant and equal to the energy altitude .
Unsteadiness of the flow, compressibility and viscosity of the fluid can be taken into account by extending the Bernoulli equation. It is used in a wide range of applications in the design of technical pipe flows , in turbine and wind power plant construction, and in measuring devices ( pitot tube , Prandtl probe ).
history
Today the Bernoulli equation can be derived from the Navier-Stokes equations or the law of conservation of energy for the fluid elements along a streamline. However, since these connections were only found in the 19th century, Daniel Bernoulli could not refer to them in his derivation in 1738. Instead, he used the preparatory work by Evangelista Torricelli , Christiaan Huygens and Gottfried Wilhelm Leibniz .
In 1640 Torricelli transferred the Galilean law of fall to outflowing liquids, which led to Torricelli's law of discharge . Huygens recognized in 1669 that the equations for elastic collision established by René Descartes are correct if one counts the velocities taking into account their sign. Leibniz concluded in 1678 from Huygen's law of elastic collision that the product of mass and the square of the velocity, twice the kinetic energy , are identical before and after the collision.
Daniel Bernoulli published his Hydrodynamica in 1738 , see pictures, where in Caesarean section 12 he combined the results of Torricelli and Huygens on a ball of fluid (abdc in his Fig. 72). In this way he succeeded in determining the pressure of flowing fluids on walls and uncovering the role of the loss of kinetic energy, which he called vis viva , in the event of sudden changes in the flow cross section.
In 1797 the Italian physicist Giovanni Battista Venturi published his discovery that the flow rate of a liquid flowing through a pipe is inversely proportional to a changing pipe cross-section. Venturi was also able to demonstrate experimentally that the static pressure at the constrictions is lower than at the other parts, see the illustration of the Bernoulli effect below.
Bernoulli and Venturi looked at the quasi one-dimensional flow with flat cross-sections, which today is the subject of hydraulics and not hydrodynamics .
Areas of application and limitations
Strictly speaking, Bernoulli's equation only applies to points on the same streamline, which requires knowledge of the velocity field. In two technically significant cases, the restriction is not serious:
- On the one hand, along flow tubes with inlet and outlet, which are connected by a "middle" flow thread, which is thus fixed. This is the specialty of hydraulics . In the #example below, too , every fluid element must run from the surface to the outlet opening , a knowledge that is already sufficient to solve the problem.
- On the other hand, in rotation-free, laminar flows far away from the edges of the flow. Such flows can be viewed as a potential flow , in which the Bernoulli equation applies globally between any two points in the area, see the #application for the wing profile.
The Bernoulli equation can also be applied in a modified form to compressible barotropic fluids. Use is again permitted in two significant cases:
- if the density-pressure relation is of the form ρ (p, T) and the temperature field T is homogeneous, i.e. only isothermal changes of state occur, or
- if the density-pressure relation is of the form ρ (p, s) and the entropy field s is homogeneous, i.e. only isentropic changes of state take place.
On the other hand, when fluid elements go through a Carnot process along a streamline, for example , they do work and give off energy and the Bernoulli equation loses its validity.
Properties of currents according to Bernoulli and Venturi
Venturi effect
Giovanni Battista Venturi discovered the continuity equation for incompressible fluids : For a given volume flow A · v , the relation flow velocity v of a non-compressible tube flow inversely proportional to the pipe cross-section A , so that the flow through each cross section is constant, see Fig. There is Δx 1,2 = v 1,2 Δt and with the constant volume V = A 1 Δx 1 = A 2 Δx 2 follows:
This means that the speed of the fluid is greatest where the cross-section of the pipe is smallest. This effect is known colloquially as the nozzle effect . The above relationship is only valid as long as changes in density are insignificant, which is a good approximation for flow velocities far below the speed of sound, see the derivation diagram below. In the case of a supersonic flow in a nozzle , the effect is reversed: a decreasing cross-section leads to a decrease in speed and vice versa, which is explained in the last two articles and used in the Laval nozzle .
The Venturi effect becomes noticeable in everyday life, for example, when the wind increases in strength between houses.
Bernoulli effect and hydrodynamic paradox
Venturi was also able to demonstrate experimentally what the Bernoulli equation predicted, namely that the static pressure decreases at the constrictions in the Venturi nozzle , see FIG. 11 in the picture. The force to accelerate the fluid particles into the constriction is the pressure gradient force and its work p · V (specific ) leads to an increase in the kinetic energy of the fluid particles.
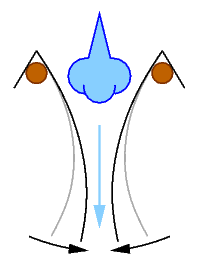
The fact that the pressure is lower at a place where the flow is faster is called the Bernoulli effect . This effect can be shown in a simple experiment, see experiment sketch: air is blown (light blue) between two sheets of paper (gray) hung over rods (brown). Due to the higher ambient pressure compared to the reduced pressure in the air stream, the leaves are compressed (black).
This fact is the hydrodynamic paradox : instead of the blown air flow pushing the leaves apart, they move together. Objects that are adjacent to flow zones of gases or liquids are drawn into them. Also, a hose that expels water and is held vertically against a wall under water is not repelled from the wall, but pulled towards the wall.
The human vocal folds are stimulated to vibrate by the Bernoulli effect, which leads to voice formation . The Bernoulli effect is used technically in jet pumps , in chimneys and when flying , see also the application below.
However, the Bernoulli effect can also have undesirable effects: If two ships are on a parallel course, the effect can distract the ships in such a way that they collide. Likewise, a ship can go aground when traveling fast and with little water under the keel because the Bernoulli effect sucks it towards the bottom. The same active principle can lead to shortness of breath in strong winds, if the wind sucks out the air that is still in the airways as a result of the Bernoulli effect. Strong winds sweeping over houses also have a reduced pressure compared to the spaces under the roof tiles , which leads to a wind load that can cover house roofs.
Further conclusions from the Bernoulli equation
The Bernoulli equation explains the following facts in a stationary, lossless and incompressible flow along a streamline:
- Pascal's Law : With a constant flow rate - especially in the rest - the pressure decreases with the height (or increases with depth) .
- Torricelli ULTRASONIC discharge law : At a constant external pressure, the square velocity increases with decreasing height (or depth increases) .
- Venturi effect: When the horizontal flow velocity squared increases in the direction of pressure increase from: .
The delta Δ stands for the difference at locations 1 and 2 on the streamline. In addition, when comparing the physical states at two points on the streamline, the following applies:
- With the same speed and the same pressure, the height at the points must also be the same.
- At the same speed and height, the pressure difference at the points is zero.
- With the same pressure and the same height, the speed is the same at the points.
application
The Bernoulli principle can be applied to many things in everyday life. Here are some examples:
- An aerator at the outlet of a water fitting sucks in air ("pearls").
- A fire brigade admixer works in a very similar way to generate extinguishing foam.
- Perfume atomizer with a rubber bubble ball.
- Airbrush brushes, compressed air spray guns for paint, oil and other things.
- Airless paint spray gun and Weingarten backpack syringe suck in air during atomization in order to distribute the liquid particles like a mist.
- Pressure differences on a wing are sufficiently well described up to speeds of approx. 300 km / h, which is an indication that the flow behaves like a potential flow in which the Bernoulli equation applies globally, i.e. between any two points in the flow area . If - as can be seen from the graphic - the threads of smoke along the top of the wing are closer together and thus the air flows faster than in other areas, then the Bernoulli equation implies that the static pressure is lower there than in the other areas. On the underside, where the threads of smoke are further apart and thus the air flows more slowly, there is a correspondingly higher static pressure. The Bernoulli equation explains the pressure differences on a wing using the streamline diagram; however, it does not explain why the current is faster on the top than the bottom. (The pressure differences are a result of the deflection of the flow; see also dynamic lift .)
- Prandtl'sches Pitot tube , which u. a. is used to measure the speed of an aircraft. Due to the presupposed incompressibility, it delivers reliable results only in subsonic flight (e.g. sports aircraft) with the same restriction.
- Water jet pump .
- Brake lip , a breathing technique for bronchial asthma and COPD .
- Intake funnel of a carburetor . The Venturi flow meter and the Venturi nozzle are also named after their inventor .
- Ventilation of ships through windscreens and Dorade fans .
- Ecological energy supply through vertical wind turbines in the Pearl River Tower (a high-rise in Guangzhou ).
The following applies to these applications:
- Since Bernoulli's law only applies along a streamline, freedom from eddies must be required in the area of the flow under consideration.
- The Bernoulli's law does not establish causality, but a relation between velocity and pressure field .
Classic formulation for incompressible fluids
Energy equation
The Bernoulli equation consists of three terms and can be clearly explained using a pipeline system for a dam and the law of conservation of energy. The energy is specified as a specific quantity , i.e. based on the mass of the fluid ( , per kg in SI units).
The first sub-term is the velocity energy e k (kinetic energy) of the fluid, which results from the flow velocity u . If the pipe narrows, the flow velocity increases according to the law of continuity and with it the kinetic energy.
If the pipeline now runs over a height difference z , the positional energy e p comes into play via the gravitational acceleration g . At the lower end of the dam, the potential energy of the flowing fluid is lower.
In order for the energy to remain constant according to the law of conservation of energy, a third sub-term, the pressure energy w p , is required in addition to the position energy and the kinetic energy . It is the work it takes to push a particle from an area of lower pressure into an area of higher pressure, as it does at the bottom of the dam. The smaller the density ρ of the particle (large volume) and the greater the pressure difference p , the more work the process requires. In the case of the funnel-shaped constriction, the constant volume flow increases the flow velocity, which means that the fluid must be accelerated by a force. This force results from the pressure in front of the constriction and reflects the pressure energy carried by each unit of mass of fluid flowing through the pipe. This results in the energy equation given at the beginning for incompressible media
Height equation
Division of the Bernoulli equation indicated by the gravitational acceleration: When the stationary (time not changing) movement of an ideal ( viscosity sfreien), incompressible liquid which is subjected only to the force of gravity, for all points of a power line the sum of velocity head , pressure altitude and constant geodetic height :
The velocity level can be understood as the dynamic pressure of the flow, the pressure level as a measure of the pressure of the liquid. This sum h , which is constant along the streamline , is called the energy level and is specified in meters.
Pressure equation
Multiplying the Bernoulli energy equation by the density ρ gives the Bernoulli pressure equation :
The total pressure p t is therefore the sum of
- the operating pressure p , which is that part of the static pressure that does not result from the dead weight of the fluid,
- the hydrostatic pressure ρ gz , which is the product of density ρ , gravitational acceleration g and height z , and
- the dynamic pressure ½ ρ u ², which is half the product of density and speed square,
constant along a streamline. From the pressure equation it can be seen, for example, that an increase in speed in a pipeline due to the narrowing of the cross-section due to the constant mass flow in the flow course must lead to a reduction in pressure if the geodetic height remains the same.
Extensions to the classic formulation
The derivation of the Bernoulli equation from the Navier-Stokes equations leads to the general Bernoulli equation in the form
In it are:
- u the speed
- the pressure function , which corresponds to the specific enthalpy for isentropic flow or p / ρ for incompressibility,
- V is the specific positional energy that takes the form V = gz in the earth's gravitational field ,
- η is a loss term that leads to pressure loss p V = ρ η in the case of incompressible flow and to loss height H V = η / g in the gravitational field of the earth , and
- a contribution that only occurs with unsteady flow.
The individual terms of this general Bernoulli equation are the subject of the following sections.
The Bernoulli equation can also be set up in a rotating frame of reference .
Extended Bernoullian pressure equation for viscosity-free, ideal gases
The Bernoulli equation given at the beginning only applies with sufficient accuracy to fluids with a negligible change in density. In the case of gases and larger changes in speed, the density changes associated with the pressure change must be taken into account in the energy approach:
The following formulations are available for the dependence of the density on the pressure:
- In isothermal or isenthalpic change of state is the specific gas constant R s and the absolute temperature T . This means that relative to a reference point 0:
- Therein ln forms the natural logarithm .
- In the case of an isentropic or adiabatic change of state , the isentropic exponent κ is relative to a reference point 0 and thus
The differential of the specific enthalpy h is d h = T d s + v d p . Here T is the absolute temperature, s the specific entropy and v = 1 / ρ the specific volume. With isentropic flow (d s = 0), d h = d p / ρ and the integrand in the Bernoulli equation above corresponds to the specific enthalpy. The Bernoulli equation for real gases with isentropic flow is thus :
Therein is the specific enthalpy.
The following relationships apply to pressure-driven equalizing flows through converging nozzles. The specific enthalpy for an ideal gas is h = c p T and with the relationships found in ideal gases it follows:
Here, c p, v are the specific heat capacities of the gas at constant pressure or constant volume.
The picture shows the enthalpy contributions h / h 0 with h 0 = R s T of air according to the given formulas and isentropic change of state (except for the isothermal change of state) relative to reference point 0 under normal conditions
With the orange curve " h = c v T " and as with the red curve " h = c p T " was used.
Extended Bernoulli energy equation for viscous liquids
The extended Bernoulli energy equation deals with viscous liquids. The friction losses are taken into account. The so-called loss height H V is usually calculated empirically using a pressure loss coefficient ( zeta ) with the following function:
With
- ζ : pressure loss coefficient
- u : speed
- g : gravitational acceleration (i.e. positional energy V = gz )
This assumption is based on the empirical observation that the pressure losses in pipelines with turbulent flow increase with the square of the flow velocity. The loss coefficients or the sum of the loss coefficients in an overall system are made up of:
- Individual losses such as inlet and outlet loss, loss of built-in components (elbows, constrictions, slides) and
- Losses from pipe friction
The pressure equation expanded by the pressure loss ρ g H V is therefore:
With this equation, the usual questions of dimensioning piping systems with turbulent flow can be solved if the loss coefficients are known.
For the calculation of the energy losses, a distinction should be made between individual losses and losses in straight pipes.
Individual losses
These are according to the formula
calculated. The pressure loss coefficients ζ are exemplary
- for inlets in pipes:
- ζ = 0.50 (vertical inlet, sharp-edged),
- ζ = 0.06 to 0.005 (vertical, rounded inlet),
- with sudden expansion of the cross-section F 1 → 2
- or
- with gradual narrowing (angle of narrowing <20 °)
- ζ = 0.04.
The parameter ζ is determined according to empirical formulas that depend on the roughness of the pipeline and the flow behavior of the medium, see pipe friction coefficient .
Losses in straight pipes
These are prepared by the so-called Darcy-Weisbach equation to
- : Energy line gradient, i.e. loss height per unit length of the pipeline.
- : Pipe friction coefficient (loss coefficient)
- : Pipe diameter
calculated.
Extended Bernoulli energy equation for unsteady flows
The contribution of speed changes over time is usually omitted in the Bernoulli equation, but can be taken into account:
The integral of the local acceleration along the streamline between points 1 and 2 is evaluated at a fixed point in time, see the example below.
The equation is significantly simplified when the flow is lossless and rotation-free or - equivalent - is a potential flow . Then there is a velocity potential φ whose gradient is the speed: . In such a flow the extended Bernoulli equation applies
even globally, i.e. for any point in the flow field. The variable C , which is constant in the entire flow field at one point in time, could still depend on the time, but this time dependency can be added to the potential φ without its physical meaning changing.
Derivation
Derivation from the energy law
The Bernoulli equation can be derived from the energy balance , which requires that work has to be done in a steady flow to change the energy of a fluid element . The work is that of pressure and the energies are the positional energy and the kinetic energy. It then shows that the sum of the pressure work (somewhat imprecise pressure energy ), the kinetic and the positional energy is constant along a streamline.
| Derivation via the energy balance |

Ball of fluid (light blue) in a stream filament ( royal blue )
|
The energy balance states that work has to be done to change the energy of the fluid elements:
Here, W is the mechanical work that has to be expended in order to generate the energy differences ΔE pot / kin between the states 2 (after) and 1 (before). The mechanical work W is the work of pressure that is required to bring a mass m = ρ V with the density ρ from the volume V with pressure p 1 into the space with pressure p 2 . The necessary force F is exerted by the pressure difference at points 1 and 2 on cross-sectional area A 1 : F = (p 1 - p 2 ) A 1 , see picture. Because the pressure p 2 also acts at the right end of the fluid ball 1. In order to push out the entire mass, this force has to work along the path s 1 with V = A 1 s 1 :
The difference in positional energy after and before is
with the heights h 1,2 . The difference in kinetic energy after and before is
with the speeds u 1.2 . Inserting these intermediate results into the energy balance provides:
Division by the volume V and conversion leads to the Bernoulli equation:
|
Today, the Bernoulli equation, in a barotropic , Newtonian fluid in a conservative gravity field from the Navier-Stokes equations are derived. The preconditions made allow the pre-integration of the gradients occurring in the Navier-Stokes equations along a streamline, which leads to the Bernoulli equation. Since the pressure-density relationship for gases is temperature dependent - gases are generally not barotropic - and often liquids are incompressible in good approximation, is usually incompressibility provided. This is a good approximation for currents far below the wave propagation speed in the fluid, see picture.
| Derived from the Navier-Stokes equations |
| The flow of a barotropic Newtonian fluid in a conservative gravity field is considered. Newtonian fluids obey the Navier-Stokes equations
In it the velocity field in the flow, the vector a volume force density such as the acceleration due to gravity , t the time, ∂ the partial derivative , Δ the Laplace operator , “·” the (formal) scalar product with the Nabla operator , which leads to the divergence of a vector field and forms the convective part of the substantial acceleration with the velocity gradient . The material parameters μ and λ are the shear viscosity and the first Lamé constant . If these are set to zero, the derivation results from the Euler equations of fluid mechanics . In a barotropic fluid, density is a function only of pressure. Then there is the pressure function P with the property In an incompressible fluid the density is constant and P = p / ρ . In a conservative acceleration field there is a potential V with the property . Furthermore, the Graßmann identity is exploited, in which "×" is the (formal) cross product of two vectors. Inserting these relationships into the Navier-Stokes equations yields after conversion: If this equation is integrated at a fixed time t along a streamline , on which by definition applies, the contribution of the last term on the right-hand side disappears and the integral yields: The loss term η is difficult to determine exactly for real flows, but it can be estimated. For a function that is only location-dependent, the following applies in a Cartesian coordinate system with x, y and z coordinates: The indices 1 and 2 mark the values at the beginning and at the end of the streamline segment under consideration. The integration of the first integral on the left-hand side can therefore be carried out at a fixed time, since the time dependence of the integrands is not relevant: After the change, the extended Bernoulli equation given in the text arises: In a steady flow the remaining integral on the right-hand side does not apply, in viscosity-free flows the loss term η disappears , in the earth's gravitational field V = gz and with incompressibility P = p / ρ . |
example
A container like the one in the picture is in the homogeneous gravitational field of the earth with gravitational acceleration g and ambient pressure p 0 and is filled with an ideal, incompressible liquid with density ρ . Let the height difference between the surface AB and the outflow o between F and D be h and the diameter FD be negligibly small compared to the surface AB and the height h . At time t 0 = 0, the outflow is opened so that the container runs out in an unsteady flow, the fill level of the container being kept constant by an inflow. Find the outflow velocity in the drain pipe as a function of time.
At a time t > t 0 , a stream filament connects the surface AB (point 1) and the outflow o (point 2). The speed in the container ACGB can be neglected because of the small diameter FD compared to AB and the speed on the cross-sections in the drainage pipe between EG and FD (over the distance L ) is the same everywhere u and its change ∂u / ∂t in the drainage pipe is also constant . The extended Bernoulli equation for unsteady flows thus yields:
This first order nonlinear ordinary differential equation can be solved by separating the variables:
Artanh is the hyperbolic areatangent and tanh is its inverse hyperbolic tangent . The velocity has the value zero at time t = 0 and asymptotically reaches the limit value for t → ∞ , which is Torricelli's law of discharge .
This law results from the Bernoulli equation faster with the assumption of a steady flow:
See also
Bernoulli effect:
- Bādgir
- Coanda effect
- Lens (optics)
- Airspeed indicator
- Harmonica instrument
- Cavitation
- sail
- Suction
- Teapot effect
Individual evidence
- ↑ Hans-Gerd Bannasch, Wolf D. Hartmann, Rainhart Kny: Maritime Clean Tech Compendium . How sustainable growth makes international success. ifi Institute for Innovation Management, 2013, ISBN 978-3-940090-12-6 , p. 130 f . ( Limited preview in Google Book Search [accessed May 1, 2017]).
- ↑ Oertel (2012), p. 60, Sigloch (2014), p. 115, Spurk (2010), p. 117, Durst (2006), p. 157.
- ↑ Pressure Energy - Lexicon of Physics. Spektrum Verlag, accessed on May 3, 2017 .
- ^ Spurk (2010), p. 117.
- ↑ Sigloch (2014), p. 115.
- ↑ Christiaan Huygens: Oeuvres Complètes . De motu corpum ex percussione. Ed .: Société Hollandaise des Sciences. tape 3 , 1929, pp. 30th ff . (French, archive.org [accessed May 1, 2017] posthumous publication).
- ↑ Gottfried Falk, Wolfgang Ruppel: Mechanics, Relativity, Gravitation . The physics of the natural scientist. Springer Verlag, Berlin, Heidelberg, New York 1973, ISBN 978-3-540-05982-0 , pp. 26th ff ., doi : 10.1007 / 978-3-642-96123-6 ( limited preview in Google Book Search [accessed on May 1, 2017]).
- ↑ Nicholas Jolley (Ed.): The Cambridge Companion to Leibniz . Cambridge University Press, 1995, ISBN 978-0-521-36769-1 (English, limited preview in Google Book Search [accessed May 1, 2017]).
- ↑ Danielis Bernoulli (1738), see literature.
- ^ A b G. K. Mikhailov: Landmark Writings in Western Mathematics 1640-1940 . Ed .: Ivor Grattan-Guinness. Elsevier, 2005, ISBN 978-0-08-045744-4 , pp. 131 ff . (English, limited preview in Google Book Search [accessed on May 1, 2017] Kindle Edition).
- ↑ Venturi (1797), see literature.
- ↑ Spurk (2010), p. 119.
- ↑ a b Spurk (2010), p. 118.
- ↑ Thomas Tredgold (1836), p. 251
- ↑ Weather and Climate. German Weather Service , October 14, 2014, accessed on September 9, 2015 .
- ↑ Jürgen Wendler, Wolfram Seidner, Ulrich Eysholdt: Textbook of Phoniatry and Pedaudiology . Georg Thieme Verlag, 2014 ( limited preview in Google Book Search [accessed June 1, 2017]).
- ↑ Bernoulli Effects - Lexicon of Physics. Spektrum Verlag, accessed May 30, 2017 .
- ↑ Holger Babinsky: How do wings work? In: Gary Williams (Ed.): Physics education . tape 38 , no. 6 . IOP Publishing (United Kingdom), November 2003 ( University of Cambridge (PDF 370 kB) [accessed April 4, 2018]).
- ↑ David Anderson, Scott Eberhardt: Understanding Flight . 1st edition. McGraw-Hill, New York et al. 2001, ISBN 978-0-07-136377-8 .
- ↑ Hermann Rietschel, Horst Esdorn, Klaus Fitzner: Indoor Climate: Volume 1: Fundamentals , Springer, 1994, ISBN 3-540-54466-6
- ↑ Spurk (2010), p. 121.
- ↑ Bernoulli's equation - Lexicon of Physics. Spektrum Verlag, accessed January 5, 2017 .
- ↑ LD Landau , EM Lifshitz : Fluid Mechanics . Course of Theoretical Physics. 3rd ed. Vol. 6. Pergamon Press, Oxford 1966, ISBN 0-08-033932-8 , pp. 9 f . ( archive.org [accessed May 16, 2017]).
-
↑ F. Durst: Fundamentals of fluid mechanics . Springer, 2006, ISBN 3-540-31323-0 , pp. 293 . see also L. J. Clancy: Aeordynamics . Wiley, 1975, ISBN 0-273-01120-0 ( limited preview in Google Book Search [accessed June 2, 2017], Chapter 3.11).
- ↑ Ralf Greve (2003), p. 147, Spurk (2010), p. 120.
- ↑ a b A. Malcherek: Hydromechanics for civil engineers. (PDF) Universität der Bundeswehr München, p. 81 , accessed on October 9, 2016 .
- ↑ Ralf Greve (2003), p. 144 f.
literature
- Danielis Bernoulli: Hydrodynamica, sive de veribus et motibus fluidorum commentarii . 1738 (Latin, archive.org [accessed May 1, 2017]). or Daniel Bernoulli: Hydrodynamics: or comments on the forces and movements of fluids . Research Institute for the History of Natural Sciences and Technology, 1965 ( limited preview in Google Book Search [accessed May 1, 2017]).
- Giovanni Battista Venturi: Recherches expérimentales sur le principe de la communication latérale du mouvement dans les fluides: appliqué à l'explication de différens phénomènes hydrauliques . Paris 1797, OCLC 15341820 ( wikimedia.org [accessed May 17, 2017] plate p. 97). English translation by Thomas Tredgold from 1836 in: Giovanni Battista Venturi: Experimental inquiries concerning the principle of the lateral communication of motion in fluids applied to the explanation of various hydraulic phenomena . printed by James Moyers, London 1836, p.
131-184, plate p. 238 ( archive.org [accessed May 2, 2017]). - Ludwig Prandtl : Prandtl guide through fluid mechanics . Fundamentals and phenomena. Ed .: H. Oertel. 13th edition. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5 .
- JH Spurk: Fluid Mechanics . 8th edition. Springer Verlag, Heidelberg, Dordrecht, London, New York 2010, ISBN 978-3-642-13142-4 , pp. 177 ff ., doi : 10.1007 / 978-3-642-13143-1 ( limited preview in the Google book search [accessed on March 17, 2020] The preview refers to the fourth edition from 1996.).
- Ralf Greve: Continuum Mechanics . Springer, 2003, ISBN 3-540-00760-1 , pp. 143 ff .
- Dieter Meschede (Ed.): Gerthsen Physik . 24th, revised edition. Springer, Heidelberg a. a. 2010, ISBN 978-3-642-12893-6 .
- H. Sigloch: Technical fluid mechanics . Springer Vieweg, Berlin, Heidelberg 2014, ISBN 978-3-642-54291-6 , pp. 115 , doi : 10.1007 / 978-3-642-54292-3 ( limited preview in Google book search [accessed March 17, 2020]).
- F. Durst: Fundamentals of Fluid Mechanics . Springer, 2006, ISBN 3-540-31323-0 , pp. 62 f.} .
- George K. Batchelor : An introduction to fluid mechanics . 1st Cambridge mathematical ed., 14th print. Cambridge University Press, Cambridge u. a. 2010, ISBN 978-0-521-66396-0 .
Web links
- Video: Ideal flow, Bernoulli and continuity equation . Jakob Günter Lauth (SciFox) 2019, made available by the Technical Information Library (TIB), doi : 10.5446 / 40453 .


























![{\ displaystyle {\ begin {aligned} \ underbrace {e} _ {\ begin {array} {c} {\ text {specific}} \\ [- 1ex] {\ text {total energy}} \ end {array}} = & \ underbrace {\ frac {u ^ {2}} {2}} _ {\ begin {array} {c} {\ text {specific}} \\ [- 1ex] {\ text {speed -}} \ \ [- 1ex] {\ text {energy}} e _ {\ text {k}} \ end {array}} + \ underbrace {\ frac {p} {\ rho}} _ {\ begin {array} {c} {\ text {specific}} \\ [- 1ex] {\ text {pressure energy}} \\ [- 1ex] w _ {\ text {p}} \ end {array}} + \ underbrace {g \, z} _ {\ begin {array} {c} {\ text {specific}} \\ [- 1ex] {\ text {positional energy}} \\ [- 1ex] e _ {\ text {p}} \ end {array}} \ \ = & {\ text {constant along a streamline}} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f94d115b42387f8f05947b54293a0a8390c82776)









![{\ displaystyle {\ begin {aligned} \ int {\ frac {\ mathrm {d} p} {\ rho (p)}} = & {\ frac {\ kappa} {\ kappa -1}} {\ frac { p_ {0}} {\ rho _ {0}}} \ left [\ left ({\ frac {p} {p_ {0}}} \ right) ^ {\ frac {\ kappa -1} {\ kappa} } -1 \ right] \\\ rightarrow \; e = & {\ frac {u ^ {2}} {2}} + {\ frac {\ kappa} {\ kappa -1}} {\ frac {p_ { 0}} {\ rho _ {0}}} \ left [\ left ({\ frac {p} {p_ {0}}} \ right) ^ {\ frac {\ kappa -1} {\ kappa}} - 1 \ right] + V \\ = & {\ text {constant along a streamline}} \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6660bb36aab6b581baa32e951d2419db15d1246b)






















![{\ displaystyle {\ frac {\ partial {\ vec {u}}} {\ partial t}} + ({\ vec {u}} \ cdot \ nabla) {\ vec {u}} = - {\ frac { \ nabla p} {\ rho}} + {\ vec {k}} + {\ frac {1} {\ rho}} [\ mu \ Delta {\ vec {u}} + (\ lambda + \ mu) \ nabla (\ nabla \ cdot {\ vec {u}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98517c537814b1527e94cad2bae85ede6e73611b)









![{\ displaystyle \ nabla \ left ({\ frac {1} {2}} {\ vec {u}} \ cdot {\ vec {u}} + P + V \ right) + {\ frac {\ partial {\ vec {u}}} {\ partial t}} = {\ frac {1} {\ rho}} [\ mu \ Delta {\ vec {u}} + (\ lambda + \ mu) \ nabla (\ nabla \ cdot {\ vec {u}})] + {\ vec {u}} \ times (\ nabla \ times {\ vec {u}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/308968509debcdc1ac1c9f0f22a1e37796d663fb)
![{\ displaystyle \ gamma \ colon s \ in [s_ {1}, s_ {2}] \ mapsto {\ vec {x}} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49eac0471cb1fa1ef2b1297e90d9304a9b5c12b5)

![{\ displaystyle {\ begin {aligned} \ int _ {\ gamma} \ nabla \ left ({\ frac {1} {2}} {\ vec {u}} \ cdot {\ vec {u}} + P + V \ right) \ cdot \ mathrm {d} {\ vec {x}} + \ int _ {\ gamma} {\ frac {\ partial {\ vec {u}}} {\ partial t}} \ cdot \ mathrm {d} {\ vec {x}} \ qquad \ qquad \ qquad \\ = \ int _ {\ gamma} {\ frac {1} {\ rho}} [\ mu \ Delta {\ vec {u}} + (\ lambda + \ mu) \ nabla (\ nabla \ cdot {\ vec {u}})] \ cdot \ mathrm {d} {\ vec {x}} =: - \ eta \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e93abfc8150497c5b2da1bdad6f028218be5bd5f)








