Disturbed gamma-gamma angle correlation
The disturbed γ-γ angle correlation , PAC for short ( English perturbed angular correlation ) or PAC spectroscopy , is a method of nuclear solid-state physics with which magnetic and electric fields can be measured in crystal structures. Electric field gradients and the Larmor frequency in magnetic fields as well as dynamic effects are determined. With this very sensitive method, which only needs approx. 10–1000 billion atoms of a radioactive isotope per measurement, material properties in the local structure, phase transitions, magnetism and diffusion can be examined. The PAC method is related to nuclear magnetic resonance and the Mössbauer effect , but it does not show any signal attenuation at very high temperatures. Today the time differential PAC ( TDPAC , English time differential perturbed angular correlation ) is mainly used.
History and Development

PAC is based on a theoretical work by Donald R. Hamilton from 1940. The first successful experiment was carried out by Brady and Deutsch in 1947. In these first PAC experiments, the spin and parity of nuclear spins were essentially investigated. However, it was recognized early on that electrical and magnetic fields interact with the nuclear moment, which provided the basis for a new form of material investigation: nuclear solid-state spectroscopy.
The theory develops step by step. After Abragam and Pound published their work on the theory of PAC in 1953, which account for extranuclear fields in the theory, many studies were carried out with PAC thereafter.
In the 1960s and 1970s there was a strong increase in interest in PAC experiments, the focus of which were mainly magnetic and electric fields in crystals into which the probe cores were introduced. In the mid-1960s, ion implantation was discovered, which opened up new possibilities for sample production. The rapid electronic development of the 1970s brought significant improvements in signal processing. From the 1980s to the present day, PAC has emerged as an important method for studying and characterizing materials, e.g. B. for the investigation of semiconductor materials, intermetallic compounds, surfaces and interfaces. Lars Hemmingsen et al. recently also used PAC in biological systems.
While PAC instruments used conventional high-frequency electronics from the 1970s until around 2008, Christian Herden and Jens Röder et al. Developed the first fully digitized PAC instrument that enables extensive data analysis and the parallel use of several probes. Replicas and further developments followed.
Measuring principle
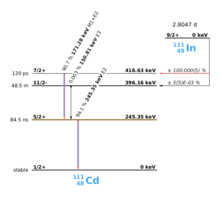
PAC uses radioactive probes that have an intermediate state with lifetimes of 2 ns to approx. 10 µs when they decay, see example 111 In in the picture on the right. After electron capture (EC ), indium transmutes to cadmium . Immediately afterwards, the cadmium nucleus is predominantly in the excited 7/2 + nuclear spin and only a very small part in the 11/2 - nuclear spin; the latter should not be considered any further. The 7/2 + excited state changes into the 5/2 + intermediate state by emitting a γ quantum with 171 keV , which has a lifetime of 84.5 ns and is the sensitive state for the PAC. This state in turn breaks down into the 1/2 + ground state by emitting a γ quantum with 245 keV. PAC now detects both γ quanta and evaluates the first as a start signal, the second as a stop signal.
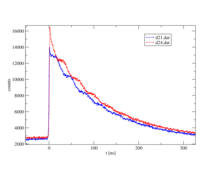
Now measure the time between start and stop for each event. One speaks of a coincidence when a start and stop pair has been found. Since the intermediate state decays according to the laws of radioactive decay , an exponential curve with the lifetime of this intermediate state is obtained after plotting the frequency over time. Due to the non-spherically symmetrical emission of the second γ-quantum, the so-called anisotropy, which is an intrinsic property of the nucleus in this transition, there is a periodic disturbance ( hyperfine interaction ) with the electric and / or magnetic fields surrounding it . The illustration of the individual spectra on the right shows the effect of this disturbance as a wave course on the exponential decay of two detectors, one pair at 90 ° and one at 180 ° to each other. The waveforms to both detector pairs are shifted against each other. In a very simplified way, one can imagine that a stationary observer is looking at a lighthouse, the light intensity of which is periodically lighter and darker. Correspondingly, a detector arrangement, mostly 4 detectors in a planar 90 ° arrangement or 6 detectors in an octahedral arrangement, “sees” the rotation of the core in the order of magnitude from MHz to GHz.
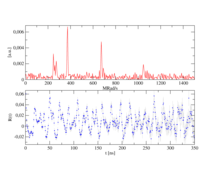
The number n of detectors results in the number of individual spectra ( z ) according to z = n ²− n , for n = 4 therefore 12 and for n = 6 thus 30. To obtain a PAC spectrum, the 90 ° - and 180 ° individual spectra are offset against each other in such a way that the exponential functions cancel each other out and the different detector properties are also reduced. The pure disturbance function remains, as shown in the example of a complex PAC spectrum. Its Fourier transformation gives the transition frequencies as peaks.
, the count rate ratio is calculated as follows:
Depending on the spin of the intermediate state, there are different numbers of transition frequencies. For 5/2 spin 3 transition frequencies can be observed with the ratio ω 1 + ω 2 = ω 3 . As a rule, a different combination of 3 frequencies can be observed for each associated grid position of the unit cell .
PAC is a statistical method: each radioactive probe atom sits in its own environment. In crystals , due to the high regularity of the arrangement of the atoms or ions, the surroundings are identical or very similar, so that probes on identical grid positions experience the same disturbance variable, which can only then be measured in a PAC spectrum. On the other hand, if the probes are in very different environments, such as B. in amorphous materials, a broad frequency distribution or none at all is usually recognizable and the PAC spectrum appears flat, without a frequency curve. In the case of single crystals, depending on the orientation of the crystal in relation to the detectors, certain transition frequencies can be reduced or extinguished, as can be seen in the example of the PAC spectrum of zinc oxide (ZnO).
Instrumental structure
In the typical PAC spectrometer, 4 detectors in a planar 90 ° and 180 ° arrangement or 6 detectors in an octahedral arrangement are placed around the sample with the radioactive source. Scintillation crystals made of BaF 2 or NaI are used as detectors . Today LaBr 3 : Ce or CeBr 3 are predominantly used in modern instruments . Photomultiplier convert the weak flashes of light into electrical signals that were generated in the scintillator by gamma radiation . In classic instruments, these signals are amplified and in logical AND / OR circuits in combination with time windows for the various detector combinations (for 4 detectors: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43) assigned and counted. Modern digital spectrometers use digitizer cards that use the signal directly and convert it into energy and time values and store them on hard drives. These are then searched for coincidences by software. While with classical instruments for the respective γ-energies limiting "windows" have to be set before processing, with the digital PAC this is not necessary during the recording of the measurement and only takes place in the analysis step. In the case of probes with complex cascades, it is possible to optimize the data or to evaluate several cascades in parallel and to measure different probes at the same time. The resulting data volumes can be between 60 and 300 GB per measurement.
Sample materials
In principle, all materials that can be solid or liquid are suitable as materials for the investigation (samples). Depending on the question and the objective of the investigation, certain framework conditions arise. For the observation of clear interference frequencies it is necessary due to the statistical method that a certain proportion of the probe atoms is in a similar environment and z. B. experiences the same electric field gradient. Furthermore, the direction of the electric field gradient must not change during the time window between the start and stop, or roughly approx. 5 half-lives of the intermediate state. Because of the frequent collisions, no interference frequency can be measured in liquids, unless the probe is complexed in large molecules, such as B. in proteins. The samples with proteins or peptides are usually frozen to improve the measurement.
The most widely studied materials with PAC are solids such as semiconductors , metals , insulators, and various types of functional materials. These are mostly available in crystalline form for the examinations . Amorphous materials do not have any highly ordered structures. However, they have a short-range order that can show up in PAC spectroscopy as a broad distribution of frequencies. According to the core-shell model, nano-materials have a crystalline core and a shell, which has a more amorphous structure. The smaller the nanoparticle, the greater the volume fraction of this amorphous fraction. In PAC measurements, this shows with the decrease in the crystalline frequency component in a decrease in the amplitude (damping).
Sample production
The amount of suitable PAC isotopes required for a measurement is between approx. 10 to 1000 billion atoms (10 10 –10 12 ). The correct amount depends on the particular properties of the isotope. 10 billion atoms is a very small amount of matter. For comparison, one mole contains about 6.22 · 10 23 particles. 10 12 atoms in one cubic centimeter of beryllium result in a concentration of approx. 8 nmol / L (nanomol = 10 −9 mol). The radioactive samples each have an activity of 0.1-5 MBq , which is in the range of the exemption limit for the respective isotope.
How the PAC isotopes are brought into the sample to be examined is up to the experimenter and the technical possibilities. The following methods are common:
implantation

During the implantation , a radioactive ion beam is generated which is directed onto the sample material, such as B. to ISOLDE . The kinetic energy of the ions (1–500 keV ) causes them to fly into the crystal lattice and are slowed down by impacts. They either come to a standstill on interstitial sites or push a lattice atom out of its place and replace it. This leads to a disruption of the crystal structure. These disorders can be investigated with PAC. These disorders can be cured by tempering. If, on the other hand, radiation defects in the crystal and their healing are to be examined, unhealed samples are measured, which are then gradually healed.
Implantation is usually the method of choice because it can be used to produce very well-defined samples.
Over-steam
The PAC probe can be evaporated onto the sample in a vacuum. The radioactive probe is applied to a heating plate or filament, brought to the evaporation temperature and condensed on the opposite sample material. With this method z. B. Surfaces are examined. Furthermore, interfaces can be produced by vapor deposition of other materials, the behavior of which can be studied with PAC during tempering. The PAC probe can also be transferred during sputtering with the aid of a plasma .
diffusion
With the diffusion method, the radioactive probe is usually diluted in a solvent and applied to the sample, dried and then diffused into the material by tempering it. The solution with the radioactive probe should be as pure as possible, since all other substances can also diffuse into the sample and this affects the measurement result. The sample should be sufficiently diluted in the sample. The diffusion process should therefore be planned in such a way that the most even distribution possible or sufficient penetration depth is achieved.
Incorporation during synthesis
PAC probes can also be added during the synthesis of sample materials in order to achieve the most even distribution possible in the sample. This method is particularly suitable if, for example, the PAC probe diffuses poorly in the material and a higher concentration at grain boundaries is to be expected. Since PAC only requires very small samples (approx. 5 mm), micro-approaches can be used. Ideally, the probe is added to the liquid phase of the sol-gel process or to one of the later precursor phases.
Neutron activation
With neutron activation , the probe is produced directly from the sample material by converting a very small fraction of one of the elements of the sample material into the desired PAC probe or its parent isotope by neutron capture. As with implantation, radiation damage must be healed. This method is limited to sample materials that contain elements from which PAC probes can be produced by neutron capture. Furthermore, samples can be specifically contaminated with elements that are to be activated. For example, hafnium is ideally suited for activation because of its large capture cross-section for neutrons.
Nuclear reactions
Direct nuclear reactions , in which nuclei are converted into PAC probes by bombardment with high-energy elementary particles or protons , are rarely used . This results in major radiation damage that must be healed. This method is used with PAD, which is one of the PAC methods.
Laboratories
The currently largest PAC laboratory in the world is located at ISOLDE in CERN with around 10 instruments, which is largely funded by the BMBF . At the ISOLDE, radioactive ion beams are produced by shooting protons from the booster onto target materials ( uranium carbide , liquid tin , etc.) and evaporating the spallation products at high temperatures (up to 2000 ° C), then ionizing them and then accelerating them. With the subsequent mass separation, very pure isotope beams can usually be produced, which can be implanted in PAC samples. Of particular interest for the PAC there are short-lived probes such as: 111m Cd, 199m Hg, 204m Pb, as well as various rare earth probes.
theory
The first quantum ( ) is emitted isotopically. By detecting this quantum in a detector, a subset is sought out of the many possible directions that has a given orientation. The second quantum ( ) is emitted anisotopically and shows the effect of the angle correlation. The aim is to determine relative probability with the detection of a fixed angle in relation to ( perturbation theory ). The probability is given by the angle correlation:
For a - cascade, precisely because of the conservation of parity as well as:
It is the spin of the intermediate state, and with the multi-polarity of the two transitions. For pure multipole transitions is .
is the anisotropy coefficient, which depends on the angular momentum of the intermediate state and the multipolarities of the transition.
The radioactive nucleus is built into the sample material for investigations and emits two quanta when it decays . During the lifetime of the intermediate state, i.e. the time between and , the nucleus experiences a disturbance due to the hyperfine interaction from its electrical and magnetic environment. This disturbance changes the angle correlation according to:
is the disruptive factor. Due to the electrical and magnetic interaction, the angular momentum of the intermediate state experiences a torque around its axis of symmetry. In terms of quantum mechanics, this means that the interaction leads to transitions between the M-states. The second quant ( ) is then sent out from a level with a changed population. This population change is the reason for the damping of the correlation.
The interaction takes place between the magnetic core dipole moment and the intermediate state and / or an external magnetic field . The interaction also takes place between the nuclear quadrupole moment and the extra-nuclear electric field gradient .
Magnetic dipole interaction
For the magnetic dipole interaction, the frequency of the precession of the nuclear spin around the axis of the magnetic field is :
is the Landé factor and is the nuclear magneton .
With results:
From the general theory we get:
The following then results for the magnetic interaction:
Static electrical quadrupole interaction
The energy of the electrical hyperfine interaction between the charge distribution of the nucleus and the extranuclear static electric field can be expanded to multipoles. The monopole term only causes an energy shift and the dipole term disappears, so that the first relevant expansion term is the quadrupole term:
- ij = 1; 2; 3
This can be written as the product of the quadrupole moment and the electric field gradient . Both tensors are of second order. Higher orders have too little effect to be measured with PAC.
The electric field gradient is the second derivative of the electric potential at the core:
is diagonalized so that:
The matrix is free of traces in the main axis system ( Laplace equation ):
Usually the electric field gradient is defined with the largest share and :
- ,
In cubic crystals, the axis parameters of the unit cell x, y, z are of equal length. Therefore is also and In axially symmetric systems is also .
For axially symmetric electric field gradients, the energy of the substates takes on the values:
The energy difference between two substates, and , is given by:
The quadrupole frequency is introduced. The formulas in the colored frames are important for the evaluation:
Most of the publications are given. the elementary charge and the Planck constant are well known or firmly defined. The nuclear quadrupole moment is often only very imprecisely determined (often only with 2–3 digits). Since it can be determined much more precisely than it does not make sense to just state because of the error propagation . In addition, is independent of the spin! This means that measurements of two isotopes of the same element can be compared with one another, e.g. B. 199m Hg (5 / 2−), 197m Hg (5 / 2−) and 201m Hg (9 / 2−). It can also be used as a fingerprint method.
The energy difference then results from:
If is, the following applies:
With:
The following applies to integer spins:
- and
The following applies to half spins:
- and
The following results for the interference factor:
with the factor for the weighting of the observed frequencies:
As for the magnetic dipole interaction, the electrical quadrupole interaction also induces precision of the angular correlation in time and this modulates the quadrupole interaction frequency. This frequency is an overlap of the various crossover frequencies . The relative amplitudes of the various components depend on the alignment of the electric field gradient relative to the detectors (axis of symmetry) and on the asymmetry parameter . For an investigation with different nuclei one needs a parameter that enables a direct comparison: Therefore the quadrupole coupling constant independent of nuclear spin is introduced.
Combined interaction
If there is a magnetic and an electrical interaction at the same time on the radioactive core, combined interactions result as described above. This leads to splitting of the frequencies observed in each case. The analysis may not be trivial due to the large number of frequencies that must be assigned. These then depend on the direction of the electrical and magnetic fields in relation to each other in the crystal. PAC is one of the few methods that can be used to determine these directions.
Dynamic interactions
If the hyperfine field fluctuates during the lifetime of the intermediate level due to jumps of the probe into another lattice position or jumps of a nearby atom into another lattice position, the correlation is lost. For the simple case with an undisturbed lattice of cubic symmetry, an exponential damping of the static term applies for a jump rate of for equivalent places :
Here is a constant to be determined that must not be confused with the decay constant . With large values of , only the pure exponential decrease can be observed:
The limit case according to Abragam-Pound results for if :
Aftermath of transmutation
Nuclei that transmute before the - cascade usually lead to a charge change in ionic crystals (In 3+ to Cd 2+ ). As a result, the grid has to react to these changes. Defects or neighboring ions can also migrate. The core can also be brought into higher ionization states through the high-energy decay process through the Auger effect . The normalization of the charge state then depends on the conductivity of the material. The process takes place very quickly in metals. In semiconductors and insulators this takes considerably longer. In all of these processes, the hyperfine field changes. This change falls into the - cascade, it can be used as after-effect (ger .: aftereffect observed).
The number of nuclei in state (a) in the picture on the right is depopulated both by the decay according to state (b) and according to state (c):
With:
This gives the exponential case:
For the total number of cores in the static state (c) it then follows:
The initial occupation probabilities for a static and dynamic environment are:
General theory
In general theory, the following is given for a transition :
- Minimum of
With:
Individual evidence
- ↑ Donald R. Hamilton: On Directional Correlation of Successive Quanta . In: Physical Review . tape 58 , no. 2 , July 15, 1940, p. 122-131 , doi : 10.1103 / PhysRev.58.122 .
- ^ Edward L. Brady, Martin Deutsch: Angular Correlation of Successive Gamma-Ray Quanta . In: Physical Review . tape 72 , no. 9 , November 1, 1947, p. 870-871 , doi : 10.1103 / PhysRev.72.870 .
- ^ H. Aeppli, AS Bishop, H. Frauenfelder, M. Walter, W. Zünti: Influence of the Atomic Shell on Nuclear Angular Correlation in Cd 111 . In: Physical Review . tape 82 , no. 4 , May 15, 1951, p. 550-550 , doi : 10.1103 / PhysRev.82.550 .
- ^ JW Gardner: Directional Correlation between Successive Internal Conversion Electrons . In: Proceedings of the Physical Society. Section A . tape 62 , no. December 12 , 1949, p. 763-779 , doi : 10.1088 / 0370-1298 / 62/12/302 .
- ^ Daniel S. Ling, David L. Falkoff: Interference Effects in Gamma-Gamma Angular Correlations . In: Physical Review . tape 76 , no. 11 , December 1, 1949, pp. 1639-1648 , doi : 10.1103 / PhysRev.76.1639 .
- ↑ M. Fierz: ON THE THEORY OF MULTIPOLE RADIATION . In: HELVETICA PHYSICA ACTA . tape 22 , no. 4 , 1949, pp. 489-500 .
- ↑ JA Spiers, Nat. Res. Council Canada, Publ. 1925 (1950)
- ^ JA Spiers: On the Directional Correlation of Successive Nuclear Radiations . In: Physical Review . tape 80 , no. 3 , November 1, 1950, p. 491-491 , doi : 10.1103 / PhysRev.80.491 .
- ↑ David L. Falkoff, GE Uhlenbeck: On the Directional Correlation of Successive Nuclear Radiations . In: Physical Review . tape 79 , no. 2 , July 15, 1950, p. 323-333 , doi : 10.1103 / PhysRev.79.323 .
- ^ Giulio Racah: Directional Correlation of Successive Nuclear Radiations . In: Physical Review . tape 84 , no. 5 , December 1, 1951, p. 910-912 , doi : 10.1103 / PhysRev.84.910 .
- ↑ U. Fano, Nat'l. Bureau of Standards Report 1214; U. Fano: Geometrical Characterization of Nuclear States and the Theory of Angular Correlations . In: Physical Review . tape 90 , no. 4 , May 15, 1953, p. 577-579 , doi : 10.1103 / PhysRev.90.577 .
- ↑ Stuart P. Lloyd: The Angular Correlation of Two Successive Nuclear Radiations . In: Physical Review . tape 85 , no. 5 , March 1, 1952, p. 904-911 , doi : 10.1103 / PhysRev. 85.904 .
- ↑ K. Adler: Contributions to the theory of directional correlations . In: Helv. Phys. Acta . tape 25 , 1952, pp. 235 ( e-periodica.ch ).
- ^ SR De Groot: On the theories of angular distribution and correlation of beta and gamma radiation . In: Physica . tape 18 , no. 12 , December 1, 1952, p. 1201-1214 , doi : 10.1016 / S0031-8914 (52) 80196-X .
- ^ F. Coester, JM Jauch: THEORY OF ANGULAR CORRELATIONS . In: Helvetica Physica Acta (Switzerland) . Vol: 26, February 15, 1953 ( osti.gov ).
- ↑ LC Biedenharn, ME Rose: Theory of Angular Correlation of Nuclear Radiations . In: Reviews of Modern Physics . tape 25 , no. 3 , July 1, 1953, p. 729-777 , doi : 10.1103 / RevModPhys.25.729 .
- ^ A. Abragam, RV Pound: Influence of Electric and Magnetic Fields on Angular Correlations . In: Physical Review . tape 92 , no. 4 , November 15, 1953, p. 943-962 , doi : 10.1103 / PhysRev.92.943 .
- ↑ Th. Wichert, E. Recknagel: Perturbed Angular Correlation . In: Ulrich Gonser (Ed.): Microscopic Methods in Metals (= Topics in Current Physics . Volume 40 ). Springer, Berlin / Heidelberg 1986, ISBN 978-3-642-46571-0 , p. 317-364 , doi : 10.1007 / 978-3-642-46571-0_11 .
- ^ Gary S. Collins, Steven L. Shropshire, Jiawen Fan: Perturbed γ − γ angular correlations: A spectroscopy for point defects in metals and alloys . In: Hyperfine Interactions . tape 62 , no. 1 , August 1, 1990, pp. 1-34 , doi : 10.1007 / BF02407659 .
- ↑ Th. Wichert, N. Achtziger, H. Metzner, R. Sielemann: Perturbed angular correlation . In: G. Langouche (Ed.): Hyperfine Interactions of Defects in Semiconductors . Elsevier, Amsterdam 1992, ISBN 0-444-89134-X , pp. 77 .
- ↑ Jens Röder, Klaus-Dieter Becker: Perturbed γ – γ Angular Correlation . In: Methods in Physical Chemistry . John Wiley & Sons, Ltd, 2012, ISBN 978-3-527-32745-4 , pp. 325-349 , doi : 10.1002 / 9783527636839.ch10 .
- ↑ Günter Schatz, Alois Weidinger, Manfred Deicher: Nuclear solid-state physics: Nuclear physical measurement methods and their applications . 4th edition. Vieweg + Teubner Verlag, 2010, ISBN 978-3-8351-0228-6 .
- ↑ Lars Hemmingsen, Klára Nárcisz Sas, Eva Danielsen: Biological Applications of Perturbed Angular Correlations of γ-Ray Spectroscopy . In: Chemical Reviews . tape 104 , no. 9 , September 1, 2004, p. 4027-4062 , doi : 10.1021 / cr030030v .
- ↑ C. Herden, J. Röder, JA Gardner, KD Becker: Fully digital time differential perturbed angular correlation (TDPAC) spectrometer . In: Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment . tape 594 , no. 2 , September 1, 2008, p. 155–161 , doi : 10.1016 / j.nima.2008.05.001 .
- ^ Matthias Nagl, Ulrich Vetter, Michael Uhrmacher, Hans Hofsäss: A new all-digital time differential γ-γ angular correlation spectrometer . In: Review of Scientific Instruments . tape 81 , no. 7 , July 1, 2010, p. 073501 , doi : 10.1063 / 1.3455186 .
- ↑ M. Jäger, K. Iwig, T. Butz: A user-friendly fully digital TDPAC spectrometer . In: Hyperfine Interactions . tape 198 , no. 1 , June 1, 2010, p. 167-172 , doi : 10.1007 / s10751-010-0201-8 .