Power law (statistics)

The frequency of the population of German cities (yellow) can be described by a power law: (blue). This is based on a Pareto distribution .

{\ displaystyle y = 380969 \ cdot x ^ {- 2.31}}

In mathematics are power laws (Engl. Power laws ) laws that the shape of a monomial have: . ${\ displaystyle y = a \ cdot x ^ {b}}$

They belong to the scale laws and describe the scale invariance of many natural phenomena. They occur, for example, in connection with word frequencies ( Zipf's law ) or human perception ( Stevens' power function ). Pareto distributions are also power laws.

Mathematical details

Power laws describe polynomial dependencies between two quantities and the shape ${\ displaystyle y}$ ${\ displaystyle x}$

{\ displaystyle y = a \ cdot x ^ {b} + \ dotsb}

It is the pre-factor , and the exponent of the power law, and by the indicated additional terms are assumed to be negligible and omitted. ${\ displaystyle a}$ ${\ displaystyle b}$ ${\ displaystyle + \ dotsb}$

The value of is usually less relevant - one is more interested in the exponent of the power law, as this determines whether it increases or decreases and at what speed. In particular, the prefactor can be integrated into the exponent. is converted to . ${\ displaystyle a}$ ${\ displaystyle y}$ ${\ displaystyle x}$ ${\ displaystyle y = a \ cdot x ^ {b} \,}$ ${\ displaystyle y = x ^ {b + \ log _ {x} a}}$

Examples

A double-logarithmic plot shows whether a given distribution can be approximated by a power function : If the graph of the function is a straight line, an approximation by a power function is possible. The slope of the straight line is then its exponent. A detailed derivation and example can be found in the article Pareto distribution .

Exponential growth of cities

A power law of the size distribution results from exponential growth when both the number and the extent of the objects to be measured grow exponentially. The size distribution of the objects at any given point in time then obeys a power law:

For example, let the number of cities at the time be an exponentially growing quantity: ${\ displaystyle t}$

{\ displaystyle n (t) = e ^ {\ nu t}}

The expansion of a city founded at the time is also growing exponentially: ${\ displaystyle t_ {i}}$ ${\ displaystyle t}$

{\ displaystyle k_ {i} = e ^ {\ mu (t-t_ {i})} \; \; \; (\ in {[1, \ infty [})}

The probability statement therefore applies to the expansion of the cities ${\ displaystyle k_ {i}}$

{\ displaystyle P [k_ {i} (t) <k] = P [e ^ {\ mu (t-t_ {i})} <k]}

.

By taking the logarithm and reshaping it results:

{\ displaystyle P [k_ {i} (t) <k] = P [\ mu (t-t_ {i}) <\ ln {k}] = P [t-t_ {i} <\ ln {k ^ {1 / \ mu}}] = 1-P [t_ {i} \ leq t- \ ln {k ^ {1 / \ mu}}]}

The probability at the time that a random city was founded before a chosen time is ${\ displaystyle t}$ ${\ displaystyle i}$ ${\ displaystyle t_ {0}}$

{\ displaystyle P_ {t} [t_ {i} <t_ {0}] = {\ frac {n (t_ {0})} {n (t)}} = {\ frac {e ^ {\ nut_ { 0}}} {e ^ {\ nu t}}} = e ^ {\ nu (t_ {0} -t)}}

.

If you use this formula for the calculation of the distribution function (set ), the distribution function results ${\ displaystyle t_ {0} = t- \ ln {k ^ {1 / \ mu}}}$

{\ displaystyle P [k_ {i} (t) <k] = 1-e ^ {\ nu (t- \ ln {k ^ {1 / \ mu}} - t)} = 1-e ^ {\ ln {k ^ {- \ nu / \ mu}}} = 1 - {\ frac {1} {k ^ {\ nu / \ mu}}}}

.

The associated probability density for the expansion (derivation of the distribution function; "size distribution") is therefore of the form sought:

{\ displaystyle p (k) = a \ cdot k ^ {- (1+ \ nu / \ mu)} \;, \; \; \; k \ in {[1, \ infty [}}

that means with . ${\ displaystyle a = -1- \ mu / \ nu}$

Network theory

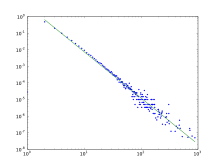
The degree distribution of a Barabási-Albert network with 200,000 nodes and a maximum degree of 882.

Power laws occur in scale-free networks , such as those generated by the Barabási-Albert model .

literature

Yule, GU : A mathematical theory of evolution based upon the conclusions of Dr JC Willis, FRS . Philos. Trans. R. Soc. Lond. B 213 : 21-87 (1924)
Willis, JC: Age and area . Cambridge Univ. Press, Cambridge 1922
Fermi, Enrico : On the Origin of the Cosmic Radiation . Phys. Rev. 75 (1949), pp. 1169-1174
Zipf, George Kingsley (1949): Human Behavior and The Principles of Least Effort . Addison-Wesley, Cambridge, MA 1949