Kinetics (chemistry)
The kinetics is a portion of the physical chemistry , which in macrokinetics is divided and Microkinetics. Microkinetics deals with the timing of chemical reactions as such. Macrokinetics considers the influence of macroscopic heat and mass transport processes on the kinetics of chemical reactions and thus represents the link between reaction kinetics and chemical reaction engineering. This article deals with the microkinetics of chemical reactions. The kinetics of electrochemical processes is covered in the article electrochemical kinetics .
Reaction speed
definition

The basic size of the kinetics of the reaction rate ( English rate of reaction ) with the dimension mole per time and volume . The unit of the reaction rate derived from the basic quantities of the international system of units is mole per cubic meter and second . The reaction rate indicates the change in the conversion variable (amount of reaction events, which are defined by the reaction equation of the reaction under consideration, in mol) per unit of time and volume under isochoric conditions. If the stoichiometric number and the amount of the stoichiometric number of a substance involved in the reaction under consideration are i , then for a reaction
the reaction rate r equals:
Here, t is the duration of the reaction, V is the reaction volume and [A], [B], [K] and [L] are the volume-related molar concentrations of the substances A, B, K and L involved in the reaction. The differential quotient is equal to the slope of the underlying concentration-time profile [A] ( t ), which represents [A] as a function of t . Since A is consumed as a starting material, the differential change in concentration d [A] and thus the differential quotient are negative. Since the stoichiometric number of a starting material also has a negative sign by convention, the expression and thus the reaction speed are positive.
Laws of speed and laws of time
The dependence of the reaction rate on the actual concentrations of the reactants in a reaction is empirically described by rate laws. Rate laws usually contain a rate constant k or a half-life t 1/2 , which represent the kinetics of the chemical process under consideration in a characteristic way. The half-life indicates the period in which the initial concentration [A] 0 of a reactant A falls to half the value.
Phenomenologically observable gross reactions can have complex reaction mechanisms that comprise sequences of several reversible elementary reactions . Examples of this are reactions that follow the Lindemann mechanism , chain reactions or enzyme-catalyzed reactions that can be described by the Michaelis-Menten theory . Furthermore, the observable rate of reaction can be influenced by competitive reactions. Since rate laws usually depict complex reaction events, conclusions cannot be drawn directly from them about the reaction mechanism. Often rate laws are formulated on the basis of simplified reaction models. For example, the kinetics of composite reactions which comprise several consecutive elementary reactions can be dominated by a particularly slow elementary reaction as the rate-determining step. In this case, the kinetics of the composite reaction are often represented in a satisfactory manner by the simpler kinetics of the particularly slow elementary reaction. If reactive intermediates occur in the course of reactions, Bodenstein's quasi-stationary principle can be applied.
Time laws indicate the conversion variable of a reaction as a function of the reaction time. Time laws are often formulated differently from this in such a way that the concentration of a substance involved in the reaction under consideration is given as a function of the reaction time without taking into account its stoichiometric number. In some cases, the time laws of chemical reactions can be determined from the respective rate laws through variable separation and integration. Conversely, the law of speed represents the first derivation of the law of time. Half-life times can be determined directly from the laws of time.
Temperature dependence of the reaction rate
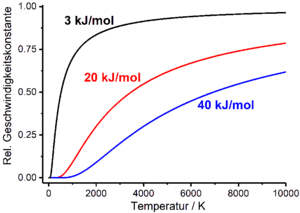
Reaction speeds basically depend on the state variables that characterize the reacting system, such as temperature T , pressure and volume. This dependency finds its way into the rate laws of chemical processes via the rate constant or the half-life, which in turn are functions of temperature, pressure and volume. In practice, the temperature dependence of the reaction rate is particularly relevant. This is empirically described by the Arrhenius equation , which relates the rate constant to temperature. The Arrhenius equation is an exponential function which contains a pre-exponential factor A with the dimension of the rate constant and the molar activation energy E A in the exponent as empirical parameters ( R is the general gas constant ):
If one assumes approximately that the pre-exponential factor of the Arrhenius equation and the activation energy are independent of the temperature, the rate constant tends towards zero when the temperature tends towards zero, and towards the pre-exponential factor when the temperature tends towards infinity. The pre-exponential factor thus represents the maximum value that the rate constant can assume.
Similarly, the Arrhenius equation can also be used to show how half-lives depend on temperature. The Arrhenius equation then has an exponent with a positive sign:
Like the half-life , the pre-exponential factor A 'has the dimension of time. The half-life approaches infinity when the temperature approaches zero, and against the pre-exponential factor when the temperature approaches infinity. The pre-exponential factor thus represents the minimum value that the half-life can assume.
Transition states and activation energies
Transitional states
In the course of an elementary reaction event, the reacting system traverses a trajectory on a potential hypersurface, which is characterized by successive structural changes such as changes in bond angles and bond lengths. According to the theory of the transition state , a potential wall separating the starting materials and products (activation barrier) is overcome, which represents a saddle point on the potential hypersurface. The states that the reacting system goes through during the elementary reaction under consideration are most appropriately described by the applicable thermodynamic potential , which depicts the changes in entropy in the universe caused by changes in the reacting system . If pressure and temperature are kept constant, this is the free enthalpy . The saddle point is the location of the highest free enthalpy that the reacting system passes through in the course of an elementary reaction event. The state that the reacting system assumes when passing through the saddle point is called the transition state. The molar free enthalpy of activation represents the level of the potential barrier to be overcome for the conversion of the starting materials into the products, i.e. the difference between the free enthalpies of the transition state and the initial state before the start of the elementary reaction event. The size of the rate constant k out , which represents the kinetics of the conversion of the starting materials into the products, depends on (see section " Thermodynamic formulation " in the article "Theory of the transition state"):
Free enthalpies of activation and thermodynamic equilibrium

Many reactions are equilibrium reactions in which, in addition to the formation of reaction products through the forward reaction, the reverse reaction also creates new starting materials from the reaction products:
Provided the forward reaction with the molar free enthalpy of activation and the molar free enthalpy of reaction
and the reverse reaction
run exactly along the same reaction trajectory in the opposite direction, the following applies to the molar free activation enthalpy of the reverse reaction:
The rate constant of the reverse reaction k back is then:
For the ratio of k towards and k rueck follows:
Thus:
Here K is the thermodynamic equilibrium constant of the reaction under consideration. The rate constants k for the forward reaction and k back for the reverse reaction are thus coupled with each other - the ratio is determined by the thermodynamic equilibrium constant. This relationship is often misinterpreted to the effect that the equilibrium constant of an equilibrium reaction depends on the rate constants of the back and forth reactions. However, this idea is based on an incorrect pre-concept . Thermodynamic quantities, which, like the free enthalpy of reaction and the equilibrium constant, describe changes in state, depend exclusively on the initial and final state, but not on the path on which the system moves from the initial to the final state.
Activation energies
The existence of potential barriers, which have to be overcome in the course of a phenomenologically observable gross reaction during the conversion of the starting materials into the products, is empirically represented by the Arrhenius equation. In contrast to the Eyring equation resulting from the theory of the transition state, the Arrhenius equation takes into account neither the number nor the nature of the transition states to be passed through by the reacting system, but represents the potential barriers to be overcome by the phenomenological parameter activation energy. If the activation energy approaches infinity at constant temperature, the rate constant converges to zero according to the Arrhenius equation. The activation energy is equal to zero, the rate constant equal to the pre-exponential factor A . Similarly, the Arrhenius equation can also be used to show how half-lives depend on the activation energy. If the activation energy runs towards infinity at constant temperature, the half-life also runs towards infinity. If the activation energy is zero, the half-life becomes equal to the pre-exponential factor A ' .
In general, at constant temperature, the rate of reaction increases if the activation energy is reduced. In the catalysis of chemical reactions, alternative reaction trajectories are provided that lead to a reduction in the activation energy. This enables higher reaction rates to be achieved without having to increase the reaction temperature.
If concentration-time profiles are determined for a reaction at several temperatures and the respective rate constants k ( T ) are determined experimentally from these , the activation energy can also be determined. Taking the logarithm converts the Arrhenius equation into a straight line equation :
The graph of the natural logarithm ln k ( T ) of the experimentally determined rate constant k ( T ) against results in a straight line, the slope of which corresponds to the negative activation energy. The intersection of the straight line with the y-axis is the logarithm ln A of the pre-exponential factor of the Arrhenius equation.
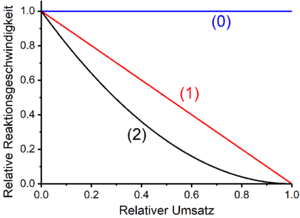
Zero to third order reactions
In many cases the rate of chemical reactions is proportional to products of power functions of the concentrations of the reactants. For a reaction involving N reactants, the rate law thus takes the following form:
The proportionality constant k is the rate constant; is the volume-related molar concentration of reactant j . The exponent is called the partial reaction order with respect to the reactant j . Partial reaction orders are not identical to the stoichiometric numbers appearing in the gross reaction equations of the processes under consideration. Partial reaction orders can, but do not have to have the same values as the stoichiometric numbers of the substances involved in a reaction. The sum of the partial reaction orders of all reactants j is the total reaction order of the reaction under consideration. Zero, first and second order reactions occur frequently, third order reactions rarely.
The time laws resulting for reactions with the first or larger overall reaction order can be converted into straight line equations by transformations (see table below ; for reactions of the zeroth order, concentration-time profiles are always linear). Time laws shown in this form can be compared with concentrations [A] ( t ) of a reactant A measured after different reaction times for the experimental determination of the overall reaction order. The amount of the slope of the straight lines obtained in this way corresponds to the speed constant k .
Overview
Time laws, the linearized plots of the time laws to determine the rate constant k and the expressions for the half-value symbols are summarized in the table below for reactions with rate laws of the type r = [A] n . The units of the rate constants k are valid for all reactions with the overall reaction order n .
| 0th order | 1st order | 2nd order | n . order | |
|---|---|---|---|---|
| Speed law | ||||
| Time law |
[ ] |
|||
| Unit k | ||||
| Linear plot of the law of time | [A] vs. t | vs. t | vs. t |
vs. t
[ ] |
| Half-life |
[ ] |
Zero order reactions
The rate of zero order reactions is independent of the concentrations of the reactants. This means that the reaction speed is constant. Time laws therefore take the form of a straight line with a negative slope (for conversion variables and reactants) or with a positive slope (for products). The slope of the straight line corresponds to the amount of the speed constant k . Examples of zero order reactions are certain photochemical and catalytic reactions . For example, the biological oxidation of ethanol to acetaldehyde by certain alcohol dehydrogenases is zero-order with respect to ethanol.
First order reactions
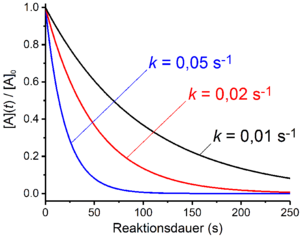
In first-order reactions, the rate of the reaction depends linearly on the concentration of a reactant A. This is the case when the overall process comprises only one unimolecular decomposition reaction. One example of this is radioactive decay . Furthermore, reactions that include several elementary reactions are of the first order if the rate-determining step is a decay or dissociation process . Examples of this are the S N 1 mechanism in nucleophilic substitution or the E1 mechanism in elimination reactions . If the amount of the stoichiometric number of the starting material A is equal to one, the rate law takes the following form for a reaction of the first order:
The first order time law is obtained by first separating the variables:
The next step is to calculate the definite integrals:
First you get:
Antilogarithming gives the time law for first-order reactions:
Second order reactions
Second order are elementary reactions based on bimolecular collisions. Examples of this are nucleophilic substitutions according to the S N 2 mechanism and eliminations according to the E2 mechanism. If first-order decay or dissociation processes also occur in the course of a multi-step reaction, these are usually the rate-determining steps, so that, as in the case of S N 1 and E1 reactions, the overall reaction is first order.
If the bimolecular collision takes place with the participation of two similar particles of species A, the amount of the stoichiometric number of the starting material A is equal to two, and the reaction equation has the form:
The resulting rate and time laws and the expression for the half-life of [A] ( t ) are listed in the table above .
If particles of two different species A and B are involved in the bimolecular collision and the absolute values of the stoichiometric numbers and the reactants A and B are both equal to one, the reaction equation becomes:
The law of speed becomes accordingly:
As a time law, one obtains with [B] 0 as the starting concentration of reactant B before the start of the reaction:
Third order reactions
For a reaction to be of the third order, it must include a trimolecular collision as an elementary reaction. Since trimolecular collisions have a low probability, third-order reactions are rare. The occurrence of reactions of the third order was roughly related to recombination reactions of atoms and radicals of the type
- ,
where M acts as a collision partner, as well as for reactions of nitrogen monoxide with halogens X and oxygen according to
and
postulated.
Rate laws of equilibrium reactions
An equilibrium reaction is considered
- .
If the back and forth reactions are first order, the changes in concentrations and are determined by the differential equations
with the rate constants of the reaction and the reverse reaction , as well as the condition
The following boundary conditions are necessary to solve this differential equation system:
- : ,
- : ,
The two differential equations for and are simplified by this boundary condition to:
This results in the following integral time law for the first order equilibrium reactions:
With
- and
such as
the following speed laws result:
Measurement of concentration-time profiles
The kinetics of chemical reactions are experimentally investigated by determining concentration-time profiles using quantitative analytical methods. For this purpose, analytical chemistry provides a wide range of methods that is continuously developing due to the progress of instrumental analysis and microreaction technology . The measured variable selected to determine the concentration-time profile should be quantitatively proportional to the concentration of the observed components. Frequently used methods for determining concentration-time profiles include the measurement of the dielectric constant , the refractive index , the optical activity , the fluorescence or the conductivity of the reaction solution, the measurement of volume or pressure changes, calorimetry as well as absorption and emission spectroscopy and light scattering .
The measured variable can be observed on the reaction mixture itself without contact and without taking samples from the reaction mixture. This procedure is advantageous because it minimizes disruptions in the course of the reaction. Another procedure is based on the fact that aliquots are taken regularly and mostly automatically from the reaction mixture . These can be subjected to non-destructive analysis methods and then combined again with the reaction mixture. Analysis methods can also be used which are associated with the consumption of the removed aliquots. If aliquots are taken from the reaction mixture, one intervenes more strongly in the reaction process than with contact-free methods. However, it is advantageous that a much broader spectrum of analytical methods can be used and analytical methods can be used that are either more sensitive or otherwise provide more information than the analytical methods that can be used for non-contact observation of the reaction mixture. The extracted aliquots can also be subjected to more complex qualitative analysis, for example by separating their components using gas chromatography or high-performance liquid chromatography before the actual analytical examination . Under certain circumstances, the reaction in the removed aliquots must be slowed down or brought to a standstill in order to prevent falsification of the analytical results due to the reaction continuing after the sample has been taken. This can be done by strongly cooling the removed reaction mixture or by removing a reactive component from the reaction mixture, for example by precipitation .
To measure concentration-time profiles, sufficient mixing of the reactants must take place so quickly that a defined starting time for the reaction to be investigated can be identified. This can be achieved by miniaturizing the experimental setups used by using microreaction technology, since the transport routes for the reactants are then shortened. In the case of slow reactions, defined amounts of material can be mixed using simple stirrers, flow tubes or high-precision mixing chambers. In the case of faster reactions, which are characterized by time scales in the minutes to seconds range, special flow devices are often used. In the case of extremely fast reactions, which are characterized by time scales in the millisecond range, optimized processes, such as the stopped-flow method , are used for fast and efficient mixing of the starting materials .
A second group of methods for investigating extremely fast reactions with characteristic time scales down to the picosecond range are relaxation methods . These are based on the principle of mixing the starting materials well before the actual observation period. The reaction mixture begins to react. After a state of equilibrium has been established in the reaction mixture, this is disturbed by a rapidly applied shock and the relaxation of the reaction mixture into a new state of equilibrium is followed with suitable analytical methods. Examples of relaxation processes are flash photolysis as well as temperature, pressure and field jump processes.
History of the kinetics
The first qualitative investigations into kinetics were reported by Carl Friedrich Wenzel as early as 1777 in his work, The Teaching of the Relationship of Bodies , published in Dresden . Later, Claude-Louis Berthollet and William Higgins also dealt with kinetic issues. The first really fundamental work on kinetics, the cleavage of cane sugar under the influence of acid, was presented by Ludwig Ferdinand Wilhelmy in 1850. Jacobus Henricus van't Hoff investigated the saponification of ethyl acetate and the hydrolysis of chloroacetic acid in 1896 . Mathematically, he formulated the rate equations for reactions. He also developed the fundamental laws on the temperature dependence of the reaction rate. Svante Arrhenius improved the derivation and gave as a rule of thumb for the change in the reaction rate when the temperature increased by 1 K an increase in the reaction rate of approx. 12% (see RGT rule ). FEC Scheffer and WF Brandsma introduced the standard Gibbs activation energy for the rate constant in 1926. Manfred Eigen , Ronald Norrish and George Porter received the Nobel Prize in Chemistry in 1967 for the development of relaxation methods to study the kinetics of fast reactions .
Individual evidence
- ↑ Entry on rate of reaction . In: IUPAC Compendium of Chemical Terminology (the “Gold Book”) . doi : 10.1351 / goldbook.R05156 Version: 2.3.3.
- ↑ DIN 13345-1978-08 Thermodynamics and kinetics of chemical reactions: symbols, units.
- ↑ Christos Capellos, Benon HJ Bielski: Kinetic systems: mathematical description of chemical kinetics in solution . Wiley-Interscience, 1972, ISBN 0471134503 , 9780471134503.
- ^ Robert G. Mortimer: Physical Chemistry . Academic Press, 2000, 2nd Edition, Chapter 12 The Rates of Chemical Reactions , p. 408.
- ↑ Ignacio Tinoco Jr., James C. Wang: Physical chemistry: principles and applications in biological sciences . Prentice Hall, 1995, 3rd edition, p. 331, ISBN 9780131865457 .
- ^ Lothar Papula: Exercises and application of mathematics for chemists. Enke Verlag, 1977, pp. 382-385.
- ↑ Klaus H. Homann: 13. Trimolecular reactions . Pp. 100-107, in reaction kinetics , Steinkopff-Verlag, Heidelberg 1975, DOI 10.1007 / 978-3-642-72314-8_13, https://doi.org/10.1007/978-3-642-72314-8_13 .
- ↑ VA Kritsman: Ludwig Wilhelmy, Jacobus Henricus van't Hoff, Svante Arrhenius and the history of chemical kinetics. In: Chemistry in Our Time. Verlag Chemie, 6/1997, p. 291 ff.
- ↑ L. Wilhelmy: About the law according to which the action of acids on cane sugar takes place. In: Pogg. Ann. 81, 1850, pp. 413-433, 499-526.
- ↑ JH van't Hoff: Studies on chemical dynamics. W. Engelmann, Leipzig 1896.
- ^ FEC Scheffer, WF Brandsma: On reaction velocities . In: Recueil des Travaux Chimiques des Pays-Bas 1926, 45, 522-534, DOI 10.1002 / recl.19260450710.
literature
General textbooks
kinetics
- Manual of Experimental Chemistry. Upper secondary level, volume 8: Kinetics, reaction mechanisms, catalysis. Aulis Verlag Deubner & Co., Cologne.
- JI Steinfeld, JS Francisco, WL Hase: Chemical Kinetics and Dynamics. 2nd Edition. Prentice Hall, 1998, ISBN 0-13-737123-3 .
- MJ Pilling, PW Seakins: Reaction Kinetics. Oxford University Press, 1995, ISBN 0-19-855527-X .
Web links
- GJ Lauth: Introduction to reaction kinetics . Lecture series, video recordings, 2013.


![{\ displaystyle \ mathrm {d ([A] / [A]} _ {0}) / \ mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bffa3007e4f2b8f970aaa310799672465021225b)
![{\ displaystyle 1 / \ nu _ {A} \ cdot \ mathrm {d ([A] / [A]} _ {0}) / \ mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e3ca75e45481f55ca495e47bbe4b3be7bc7732e)
![{\ displaystyle [A] _ {0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32488af10ddcce5bf90dbc659e6472d1279bd2f0)

![{\ displaystyle \ mathrm {[A]} (t) / \ mathrm {[A]} _ {0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca8e698d211a4ba286dc5cee735fa102b7a7bd55)





![{\ displaystyle r = {\ frac {\ mathrm {d} \ xi} {V \ mathrm {d} t}} = {\ frac {1} {\ nu _ {\ mathrm {A}}}} {\ frac {\ mathrm {d} [\ mathrm {A}]} {\ mathrm {d} t}} = {\ frac {1} {\ nu _ {\ mathrm {B}}}} {\ frac {\ mathrm { d} [\ mathrm {B}]} {\ mathrm {d} t}} = {\ frac {1} {\ nu _ {\ mathrm {K}}}} {\ frac {\ mathrm {d} [\ mathrm {K}]} {\ mathrm {d} t}} = {\ frac {1} {\ nu _ {\ mathrm {L}}}} {\ frac {\ mathrm {d} [\ mathrm {L} ]} {\ mathrm {d} t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bad051803386419a21f7dea06cdb06da403dd71b)
![{\ displaystyle \ mathrm {d [A]} / \ mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9c0c0ea6e036d66d87e63ce6eb602371b86bfe5)
![{\ displaystyle 1 / \ nu _ {\ mathrm {A}} \ cdot \ mathrm {d} [\ mathrm {A}] / \ mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf7715affb2ac61f59c17ce855a4a55881e1c44f)



![{\ displaystyle k_ {hin} = {\ rm {constant}} \ cdot {\ rm {exp}} [- {\ frac {\ Delta G_ {hin} ^ {\ ddagger}} {RT}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad042d51c2ae74b61d2f177272f314f477011c35)







![{\ displaystyle k_ {back} = {\ rm {constant}} \ cdot {\ rm {exp}} [- {\ frac {\ Delta G_ {back} ^ {\ ddagger}} {RT}}] = {\ rm {constant}} \ cdot {\ rm {exp}} [- {\ frac {\ Delta G_ {hin} ^ {\ ddagger} + \ Delta _ {R} G} {RT}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e65c5bf0765113086f9f2c4b77d88b8102f73475)
![{\ displaystyle {\ frac {k_ {hin}} {k_ {rueck}}} = {\ rm {exp}} [- {\ frac {\ Delta G_ {hin} ^ {\ ddagger}} {RT}}] \ cdot {\ rm {exp}} [- {\ frac {\ Delta G_ {hin} ^ {\ ddagger} + \ Delta _ {R} G} {RT}}] ^ {- 1} = {\ rm { exp}} [{\ frac {\ Delta G_ {hin} ^ {\ ddagger} + \ Delta _ {R} G} {RT}}] \ cdot {\ rm {exp}} [- {\ frac {\ Delta G_ {hin} ^ {\ ddagger}} {RT}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9694c358f85fe08abd4de37f7c2892345edb08ec)
![{\ displaystyle {\ frac {k_ {hin}} {k_ {back}}} = {\ rm {exp}} [{\ frac {\ Delta _ {R} G} {RT}}] = K}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72a13659599a99050779f36057773aa6ca4fce00)




![{\ displaystyle 1- [A] / (| \ nu _ {A} | \ cdot [A] _ {0})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337110c425d9c31781976d98d5121f691087562b)



![{\ displaystyle - {\ rm {d [{\ ce {A}}]}} / {\ rm {dt}} = k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d975a9f71636dc37467b234bad2f442ed919db7)
![{\ displaystyle - {\ rm {d [{\ ce {A}}]}} / {\ rm {dt}} = k [{\ ce {A}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0563ad013f99502c4517e1b54f914ec9898c248c)
![{\ displaystyle 1 / \ nu _ {A} \ cdot {\ rm {d [{\ ce {A}}]}} / {\ rm {dt}} = k [{\ ce {A}}] ^ { 2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cb956edfcde1d070aea237ab9ff26125b73f343)
![{\ displaystyle 1 / \ nu _ {A} \ cdot {\ rm {d [{\ ce {A}}]}} / {\ rm {dt}} = k [{\ ce {A}}] ^ { n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cff3c5b3bf2d836548eba5c053ea3d0ed8716094)
![{\ displaystyle {[A] = [A] _ {0}} - kt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab2c8059ebe0459f134ae924fac2345d733ab0f3)
![{\ displaystyle {[A] = [A] _ {0}} e ^ {- kt}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ea3505d5dea20a5ef392ab615c8ab9373954778)
![{\ displaystyle {[A] = 1 / \ {{kt} + {\ frac {1} {[A] _ {0}}} \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd6e92aba9c24e4c1b37eee5fffb4df34022dd80)
![{\ displaystyle {\ frac {1} {[A] ^ {n-1}}} = {\ frac {1} {{[A] _ {0}} ^ {n-1}}} + (n- 1) kt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86ddeeab8fb56a5beb7db803822388449c77ba59)





![{\ displaystyle {\ ce {\ ln ([A])}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8378871d4c6cf8ce28a1a4c9aff69e59ba35fc8)
![{\ displaystyle {\ ce {{\ frac {1} {[A]}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/104bf3c6ecace101c498f948eaf16bf55240619f)
![{\ displaystyle {\ ce {\ frac {1} {[A] ^ {{\ mathit {n}} - 1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cca86ad925386e3c962305fa7ad13100633146e)
![{\ displaystyle t_ {1/2} = {\ frac {[A] _ {0}} {2k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cae111b01090e6a8e67e8568716449527819d2f)

![{\ displaystyle t_ {1/2} = {\ frac {1} {k {\ ce {[A] 0}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5de98bae16a32978c375f84add754fd91555826f)
![{\ displaystyle t_ {1/2} = {\ frac {2 ^ {n-1} -1} {(n-1) k {\ ce {[A] 0}} ^ {n-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e243334643f1bbcd8dc3e7b550edec77ae045f6)

![{\ displaystyle r = - {\ frac {\ mathrm {d} [\ mathrm {A}]} {\ mathrm {d} t}} = k \ cdot [\ mathrm {A}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b4cfbb15c7e293529f6f35c2b4fbab84fafcb12)
![{\ displaystyle {\ frac {1} {[\ mathrm {A}]}} \ cdot \ mathrm {d} [\ mathrm {A}] = - k \ cdot {\ mathrm {d} t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d721e322824a3b6235e7edbcf2231a7c27964488)
![{\ displaystyle \ int _ {[A] _ {0}} ^ {[A] (t)} {\ frac {1} {[\ mathrm {A}]}} \ cdot \ mathrm {d} [\ mathrm {A}] = \ int _ {0} ^ {t} -k \ cdot {\ mathrm {d} t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b574206cc7d81f01f1b9c15bcd725f1699d29a34)
![{\ displaystyle \ mathrm {ln} \; [\ mathrm {A}] (t) - \ mathrm {ln} \; [\ mathrm {A}] _ {0} = - k \ cdot t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89064fab7d06cfe89e5e08aa5ab300e264c1b32d)
![{\ displaystyle [\ mathrm {A}] (t) = {[\ mathrm {A}] _ {0}} \ cdot e ^ {- k \ cdot t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a78f35f8e250668fc0cabf0c33a1c97395f955f)



![{\ displaystyle r = - {\ frac {\ mathrm {d} [\ mathrm {A}]} {\ mathrm {d} t}} = - {\ frac {\ mathrm {d} [\ mathrm {B}] } {\ mathrm {d} t}} = k \ cdot [\ mathrm {A}] \ cdot [\ mathrm {B}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30dca39ceaa144485ade998b5f8baaadd31e7a26)
![{\ displaystyle [\ mathrm {A}] = {\ frac {[\ mathrm {A}] _ {0} \ cdot \ {[\ mathrm {A}] _ {0} - [\ mathrm {B}] _ {0} \} \ cdot e ^ {\ {[\ mathrm {A}] _ {0} - [\ mathrm {B}] _ {0} \} kt}} {[\ mathrm {A}] _ { 0} \ cdot e ^ {\ {[\ mathrm {A}] _ {0} - [\ mathrm {B}] _ {0} \} kt} - [\ mathrm {B}] _ {0}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c86522ca944cc9278e4c68a32e067a653a26cdd4)






![{\ displaystyle v_ {a} = {\ frac {d \ mathrm {[A]}} {dt}} = - k_ {ab} \ cdot [\ mathrm {A}] + k_ {ba} \ cdot [\ mathrm {B}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af96a7e8675a965f0b134062ae24036fb056e8b9)
![{\ displaystyle v_ {b} = {\ frac {d \ mathrm {[B]}} {dt}} = + k_ {ab} \ cdot [\ mathrm {A}] -k_ {ba} \ cdot [\ mathrm {B}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5c0531a99437256421b569a7844d679ab003005)




![{\ displaystyle {d \ mathrm {[A]}} + {d \ mathrm {[B]}} = 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70a42f4d2ae1ea911a725832dce50211ae052a86)

![{\ displaystyle \ mathrm {[A]} = \ mathrm {[A]} _ {0} -x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4401e232423ffc963599d5f2f5e70a8f344e245e)
![{\ displaystyle \ mathrm {[B]} = \ mathrm {[B]} _ {0} + x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72ee410f2ae3fa77a5531f88e17c2dc9182b43e7)

![{\ displaystyle \ mathrm {[A]} _ {eq} = \ mathrm {[A]} _ {0} -x_ {eq}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b20bf5d86ff2aab02b8ca424ff5c594c540b1ef)
![{\ displaystyle \ mathrm {[B]} _ {eq} = \ mathrm {[B]} _ {0} -x_ {eq}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7df9120d9a4c86ef1c95629ca819fcf6f5289fd6)


![{\ displaystyle \ mathrm {[A]} _ {eq} = (\ mathrm {[A]} _ {0} + \ mathrm {[B]} _ {0}) \ cdot {\ frac {k_ {ba} } {k_ {ab} + k_ {ba}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c770f054697f12a02a16be5aeb03939c1dd4fce4)
![{\ displaystyle \ mathrm {[B]} _ {eq} = (\ mathrm {[A]} _ {0} + \ mathrm {[B]} _ {0}) \ cdot {\ frac {k_ {ab} } {k_ {ab} + k_ {ba}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/075da07ade684dc9afc5e6b6fb2d232a821d6d69)
![{\ displaystyle \ mathrm {[A]} _ {0} - \ mathrm {[A]} _ {eq} = \ mathrm {[B]} _ {eq} - \ mathrm {[B]} _ {0} = {\ frac {k_ {ab} \ mathrm {[A]} _ {0} -k_ {ba} \ mathrm {[B]} _ {0}} {k_ {ab} + k_ {ba}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b965ff8af4fc9e9a343aba18e0e263f455eae0)
![{\ displaystyle \ mathrm {[A]} _ {t} = (\ mathrm {[A]} _ {0} + \ mathrm {[B]} _ {0}) \ cdot {\ frac {k_ {ba} } {k_ {ab} + k_ {ba}}} + {\ frac {k_ {ab} \ mathrm {[A]} _ {0} -k_ {ba} \ mathrm {[B]} _ {0}} {k_ {ab} + k_ {ba}}} \ cdot e ^ {- (k_ {ab} + k_ {ba}) \ cdot t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12b888fda347eb673aa18c08443b2efa0254ed02)
![{\ displaystyle \ mathrm {[B]} _ {t} = (\ mathrm {[A]} _ {0} + \ mathrm {[B]} _ {0}) \ cdot {\ frac {k_ {ab} } {k_ {ab} + k_ {ba}}} - {\ frac {k_ {ab} \ mathrm {[A]} _ {0} -k_ {ba} \ mathrm {[B]} _ {0}} {k_ {ab} + k_ {ba}}} \ cdot e ^ {- (k_ {ab} + k_ {ba}) \ cdot t}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30dc957708e0c1cecd06b7c55bdef130f88ffb8e)