Arrhenius equation
The Arrhenius equation , named after Svante Arrhenius , approximately describes a quantitative temperature dependence in physical and, above all, chemical processes in which an activation energy has to be overcome at the molecular level . The Arrhenius equation describes a phenomenological relationship and applies to a great many chemical reactions. The Arrhenius equation is related to the Eyring equation , which is a connection between the microscopic interpretation.
Arrhenius equation in chemical reaction kinetics
In chemical kinetics, the Arrhenius equation describes the quantitative dependence of the reaction rate constants on the temperature for the special case of monomolecular reactions :
With
- Pre-exponential or frequency factor , according to the impact theory corresponds to the product of the impact number Z and the orientation factor P :
- Activation energy (unit: J mol −1 ),
- universal gas constant (8.314 J K −1 mol −1 ),
- absolute (thermodynamic) temperature (unit: K ).
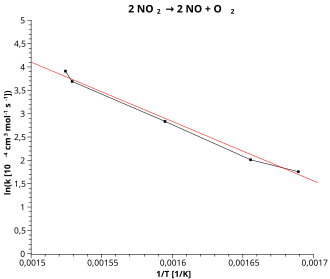
The Arrhenius graph is a reciprocal representation in which the logarithmic rate constant is plotted against the reciprocal value of the temperature ( see Fig. ):
Temperature dependence of the frequency factor
However, the Arrhenius equation is not exactly valid, because it is also temperature-dependent and often the law
follows. Thus the pre-exponential factor also increases slightly with increasing temperature ( root function ). However, its temperature dependence is significantly less than that of the exponential term. In this case a modified Arrhenius equation can be used:
With the exponent combined to form the Arrhenius number
the Arrhenius equation is also represented as follows:
Arrhenius equation in other processes
The temperature dependence of the viscosity of liquids , the charge carrier density with intrinsic conduction in semiconductors and the diffusion coefficient in solids is also described by an Arrhenius equation.
Calculation of the activation energy
By measuring two rate constants , and two temperatures of the same reaction, the activation energy can be calculated by setting up the Arrhenius equation for the two measurements as follows (assuming that A does not depend on temperature):
Taking the natural logarithm and introducing a main denominator yields:
Changing after finally results in:
An increase in temperature leads to an increase in the reaction rate. A rule of thumb , the so-called reaction rate temperature rule (RGT rule) , predicts a doubling to quadrupling of the reaction rate when the temperature rises . The factor by which the reaction rate changes with a temperature increase of 10 K is referred to as the Q 10 value.
For a -fold higher reaction speed, the following applies:
and thus:
See also
Individual evidence
- ^ Jacobus Henricus van't Hoff: Études de dynamique chimique. Frederik Muller & Co., Amsterdam 1884, pp. 114-118.
- ^ Svante Arrhenius, Z. Phys. Chem. 1889, 4 , pp. 226-248.
- ↑ Entry on Arrhenius equation . In: IUPAC Compendium of Chemical Terminology (the “Gold Book”) . doi : 10.1351 / goldbook.A00446 Version: 2.3.1.
- ↑ Entry on modified Arrhenius equation . In: IUPAC Compendium of Chemical Terminology (the “Gold Book”) . doi : 10.1351 / goldbook.M03963 Version: 2.3.1.
- ^ Charles E. Mortimer, Ulrich Müller, Chemistry - The basic knowledge of chemistry, page, 11th edition, ISBN 978-3-13-484311-8 , page 266f
- ↑ M. Binnewies, Allgemeine und Anorganische Chemie, 1st edition 2004. ISBN 3-8274-0208-5 , pp. 299f.