Arrhenius graph

An Arrhenius graph (also known as Arrhenius plot or Arrhenius plot ) is a special graphic representation of the temperature dependency of a quantity (e.g. the rate constant of a chemical reaction ), in which the logarithm of the quantity is plotted against the reciprocal of the temperature . As a result, relationships that can be described with an Arrhenius equation are shown as a straight line. This type of application is used in various chemical or physical processes.

application

Formula symbols

${\displaystyle E_{\mathrm {A} }}$	Activation energy	J mol −1
${\displaystyle k_{\mathrm {B} }}$	Boltzmann's constant	1.381e-23 J K−1
${\displaystyle R}$	universal gas constant	8.314 J mol −1 K −1
${\displaystyle N_{\mathrm {A} }}$	Avogadro's constant	6th.022e23 mol−1
${\displaystyle T}$	absolute temperature	K

Applies to size in its dependence on the temperature of the connection ${\displaystyle k}$ ${\displaystyle T}$

${\displaystyle k=k_{0}\cdot \mathrm {e} ^{-{\frac {E_{\mathrm {A} }}{k_{\mathrm {B} }\cdot T}}}\qquad }$ (for single particles with the Boltzmann constant)

or

${\displaystyle k=k_{0}\cdot \mathrm {e} ^{-{\frac {E_{\mathrm {A} }}{R\cdot T}}}\qquad }$ (macroscopically with the universal gas constant)

or for their numerical value ${\displaystyle \{k\}}$

${\displaystyle \{k\}=\{k_{0}\}\,\mathrm {e} ^{-{\frac {E_{\mathrm {A} }}{R\cdot T}}}}$

and this is logarithmized to

${\displaystyle \ln\{k\}=\ln\{k_{0}\}-{\frac {E_{\mathrm {A} }}{R}}\cdot {\frac {1}{T}}}$ ,

Decomposition nitrogen dioxide

2 NO 2 → 2 NO + O 2

Rate constant over temperature with linearly divided axes

Arrhenius graph

then this equation results with and as a straight line equation ${\displaystyle y=\ln\{k\}}$ ${\displaystyle x={\frac {1}{T}}}$

${\displaystyle y=b+m\cdot x}$

with the slope . ${\displaystyle m=-{\frac {E_{\mathrm {A} }}{R}}}$

If values ​​obtained from measurements of than over than are plotted on linearly divided axes in a Cartesian coordinate system , a straight line should result. The activation energy can be calculated from its slope . ${\displaystyle \ln\{k\}}$ ${\displaystyle y}$ ${\displaystyle {\frac {1}{T}}}$ ${\displaystyle x}$ ${\displaystyle m={\tfrac {\Delta y}{\Delta x}}}$ ${\displaystyle E_{\mathrm {A} }}$

Equivalent statements result with the decadic logarithm with

${\displaystyle y=\lg\{k\}}$, and . ${\displaystyle x={\frac {1}{T}}}$ ${\displaystyle m=-\lg \mathrm {e} \,{\frac {E_{\mathrm {A} }}{R}}=-{\frac {E_{\mathrm {A} }}{2{,}3026\;R}}}$

Examples

Laws of nature that are linearly represented in the Arrhenius graph are, for example, the temperature dependence

• the reaction rate of a first order reaction,
• the diffusion coefficient in solids and
• the intrinsic conduction density in semiconductors.

If, on the basis of theoretical considerations, a corresponding law is suspected, this assumption can be assessed with the help of the Arrhenius representation. If the Arrhenius graph is not straight, then the investigated relationship can obviously not be described by the Arrhenius equation (in kinetics: no first order reactions).

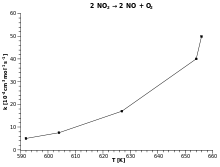
In the example opposite, the assumption of a first-order reaction is confirmed; the slope can be read off and calculated, and from this the activation energy.

swell

• Physical chemistry # literature