Half-life
The half-life or half-life (abbreviated half-life , usually symbol ) is the period of time after which a quantity that decreases over time reaches half of the initial value (or, in medicine and pharmacology, half of the maximum value).
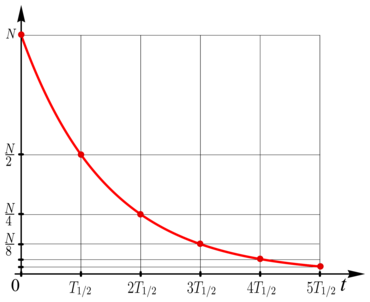
If the decrease follows an exponential law (see figure), then the half-life is always the same, even if you take the remaining amount that is left after any given time as the new initial amount. With an exponential decrease, the half-life therefore characterizes the underlying process as such.
A closely related variable is the service life . In the case of an exponential decrease, it is the period of time after which the size has decreased to the fraction 1 / e ≈ 36.8% of the initial value.
If, on the other hand, a variable increases over time, the period of time after which double the initial value is reached is referred to as the doubling time . In microbiology, the doubling time of a population is also called generation time .
Half-lives in various processes
Exponential decrease
In the case of an exponential decrease in a variable , the half-life does not depend on the choice of the starting point or on the starting value then available . In this case it is always
- after a lapse of the value ,
- after on ,
- after on ,
- generally after on
like.
Radioactive decays


The radioactive decay of a given radionuclide is exponential. The half-life is the period of time in which the amount and thus also the activity of a given radionuclide has halved due to decay. 50% of the atomic nuclei have - i. A. with emission of ionizing radiation - converted into another nuclide ; this in turn may or may not also be radioactive. For every nuclide, the half-life is a fixed value that cannot be influenced (only in exceptional cases very slightly).
However, the halving is only valid as a statistical mean . It is found to be confirmed all the more precisely, the more atoms that have not decayed are still contained in the sample under consideration. The point in time of the transformation of an individual atomic nucleus cannot be predicted, only the probability of the transformation per time interval can be specified (decay constant , see below ). The probability that a considered individual nucleus transforms within the first half-life is 50%, that it transforms within two half-lives, 50% + 25% = 75%, with three half-lives 50% + 25% + 12.5% = 87.5% etc.
There are radioactive half-lives ranging from less than a microsecond to a few quadrillion years . Polonium -212, for example, has a half-life of 0.3 µs, whereas tellurium -128 has a half-life of around 7 · 10 24 (7 quadrillion) years.
Closely related to the half-life of a radionuclide is its specific activity , i.e. the activity per mass , expressed e.g. B. Becquerels per milligram, Bq / mg. The relationship between specific activity and the half-life is inversely proportional : the shorter the half-life, the greater the activity for a given amount of substance and vice versa.
The following table contains some examples. Only the mass of the radionuclide itself is taken into account in the numerical values; In practice, specific activities tend to be related to the respective natural isotope mixture or the total material of the sample.
| isotope | Half-life | specific activity |
|---|---|---|
| 131 I. | 8 days | 4,600,000,000,000 Bq / mg |
| 3 H | 12.33 years | 370,000,000,000 Bq / mg |
| 137 Cs | 30 years | 3,300,000,000 Bq / mg |
| 239 Pu | 24,110 years | 2,307,900 Bq / mg |
| 235 U | 703,800,000 years | 80 Bq / mg |
| 238 U | 4,468,000,000 years | 12 Bq / mg |
| 232 Th | 14,050,000,000 years | 4 Bq / mg |
It was not until the end of the 20th century that some nuclides that were previously considered stable were "exposed" as extremely long-lived radionuclides, for example 149 Sm , 152 Gd (both lanthanides ), 174 Hf , 180 W and 209 Bi with half-lives of up to several trillion years . With such long half-lives, the activity is correspondingly low and can only be detected with great effort.
For some practical purposes, such as when looking at the total radioactivity inventory from a laboratory or nuclear facility , is seen as a rule of thumb, the activity of a given radiation source after 10 half-lives to be negligible, because it has then the 2 -10 times what (= 1 / 1024), i.e. less than a thousandth of the initial value.
Measurement of radioactive half-lives
Different methods are required to measure the half-life because of the different orders of magnitude.
- In a middle range, for half-lives from seconds to days, you can directly follow the decrease down to half the activity.
- Very long half-lives are measured by counting the number of decays per time interval on a known amount of the substance; so one does not determine , but the decay constant (see below). The exact amount of the radionuclide can be determined, for example, by means of mass spectroscopy . With such a method, the half-life of the iron isotope Fe-60 of 2.5 · 10 6 years has been measured with an accuracy of 2%.
- For very short half-lives there are techniques that z. B. determine the location of the decay when the atom or molecule flies past a number of detectors at a known speed, and other methods.
- Extremely short half-lives, e.g. B. of excited nuclear states in the range of 10 −22 ... 10 −16 seconds, one can measure over the decay width of the resulting radiation.
Data collections
The half-lives of all radionuclides can be found in the list of isotopes . In general, they are given in nuclide maps along with other data . The Karlsruhe Nuclide Map is a widely used printed collection. For example, a representation from the Korean Atomic Energy Research Institute is available as an online nuclide map.
history
The first observation that the activity of a radionuclide decreases by the same factor over the same periods of time - that is, can be described by a fixed half-life - was published by Rutherford in 1900 . The substance investigated by Rutherford was the radon isotope in today's designation .
Biological half-life
The biological half-life or elimination half-life (see also plasma half-life ) is the period of time in which the amount of an incorporated substance in an organism (human, animal, plant, unicellular organism) is halved due to the effect of all biological processes involved (metabolism, excretion, etc.) has sunk.
In pharmacokinetics , half-life is the time in which half of the ingested drug is metabolized and / or excreted. Pharmacokinetic half-lives can vary widely. In adults, for example, 0.5 hours are given for penicillin -G and 120 hours for phenobarbital . Since various processes with partly different concentration dependencies are involved in the decrease in quantity, the elimination half-life of some substances depends on the initial concentration; for phenytoin it is e.g. B. at low concentration seven hours, at higher concentration up to 40 hours.
Effective half-life
The effective half-life of a radionuclide is the time period within which half the amount of an incorporated (in an organism disappears recorded) radionuclide. Two processes are involved here, radioactive decay and, independently of this, re- excretion through the metabolism . Both run exponentially with mostly different half-lives. The resulting function can be described by a single exponential function and thus also by a half-life.
The effective half-life is always shorter than the smaller of the two individual half-lives. If the biological and the physical half-life are very different, the effective half-life is roughly the shorter. With half-lives of equal length, the effective half-life is half of each of the original half-lives.
Bibliometric half-lives
In bibliometrics , a more or less exponential behavior with a half-life of around five years has been established for the obsolescence of scientific publications - measured by the decreasing frequency of citations in other publications. From the usage statistics of the Ulm University Library, the same half-life was found for the frequency of orders for copies of journal articles. A scientific publication is therefore read or cited on average around 13% less often than in the previous one (apart from the classics and the latest works).
Mathematical definition
Preliminary remark:
The law of decay assumes a continuous quantity that can be represented as a real number . But it is also possible to use whole numbers such as B. the number of atoms in the radioactive substance sample can be used, because it describes the metrological expected value, i.e. the mean value over many (imaginary) individual measurements.
Exponential decay
It is believed that a process decreases the amount of a substance with a fixed decay constant . This means that the amount changes during a short period of time , i.e. the -th part of the current amount of substance decays. This results in a simple differential equation that describes this process:
This equation has an exponential function as a solution
where is the initial amount of the substance. The half-life is now the time after which only half of the substance is still present, so it applies . This results from onset
and more generally for the time after which only the -th part of the substance is present, for which the following applies
General decay
For more general decays, the definition of half-life is still the same
however, the size then no longer follows a simple exponential function.
An example of this are chemical reactions of the second order, such as dimerizations of form
in which two molecules N always combine to form one molecule P. The rate equation for this is an ordinary differential equation that describes the decay:
Here, the reaction rate constant and the reaction rate. The solution to this equation is then
and the half-life results in
In contrast to the exponential case, it depends not only on the reaction rate constant, but also explicitly on the initial quantity ; “Half-life” here always refers to the time after which the initial amount has halved. The time after which the -th part of the substance has disintegrated results in
See also
Web links
- Calculation aid for activity after selectable decay time with almost 4500 freely selectable nuclides.
Individual evidence
- ↑ Duden.
- ↑ a b c Otto-Albrecht Neumüller (Ed.): Römpps Chemie-Lexikon. Volume 3: H-L. 8th revised and expanded edition. Franckh'sche Verlagshandlung, Stuttgart 1983, ISBN 3-440-04513-7 , pp. 1612-1613.
- ↑ A. Wallner et al. a .: Physical Review Letters. Vol. 114 (2015) 041101.
- ^ EB Paul: Nuclear and Particle Physics. North-Holland 1969, pp. 47-49.
- ^ J. Magill, G. Pfennig, R. Dreher, Z. Sóti: Karlsruher Nuklidkarte. 8th edition 2012. Nucleonica GmbH 2012, ISBN 92-79-02431-0 (wall map) or ISBN 978-3-00-038392-2 (folding map).
- ↑ KAERI nuclide map.
- ^ E. Rutherford: A Radioactive Substance emitted from Thorium Compounds. In: Philosophical Magazine. Ser. 5, 49, pp. 1-14 (1900).
- ↑ Jörn Bleck-Neuhaus: Elementary Particles . From the atoms to the standard model to the Higgs boson. 2nd, revised edition. Springer, 2013, ISBN 978-3-642-32578-6 , ISSN 0937-7433 , p. 157-159 , doi : 10.1007 / 978-3-642-32579-3 .
- ^ S. Ebel, HJ Roth (Ed.): Lexicon of Pharmacy. Georg Thieme Verlag, 1987, p. 307, ISBN 3-13-672201-9 .
- ↑ a b Malcolm Rowland and Thomas N. Tozer: Clinical Pharmacokinetics. Philadelphia 1980, p. 91, ISBN 0-8121-0681-4 .
- ^ PF Cole: A new look at reference scattering. In: Journal of Documentation. 18, pp. 58-64 (1962).
- ^ W. Umstätter, M. Rehm, Z. Dorogi: The half-life in the scientific literature. ( Memento of September 27, 2011 in the Internet Archive ). In: Nachr. F. Doc. 33 (1982), pp. 50-52, accessed May 5, 2015.
- ^ Peter Atkins, Julio de Paula: Atkins' Physical Chemistry . Oxford University Press, 2010, ISBN 978-0-19-954337-3 , pp. 793-795.