Analemma
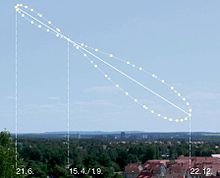
The term analemma ( Greek description, possible assumption, prescription for the base of a sundial) is most often used for the figure that the position of the sun creates with constant mean local time . This figure is created, for example, through photos of the sun that are taken daily at the same mean local time (that is also: at the same zone time in the same place) over a year . If, after a year, all these images of the sun are superimposed in a photomontage, one recognizes an elongated eight (see illustration): the analemma .
In gnomonic , the theory of sundials , the analemma is a rule given by Vitruvius for the construction of sundials.
The positions of the sun as an analemma
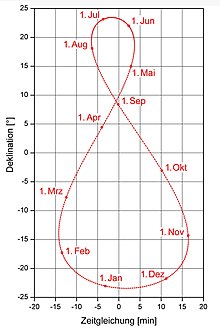
The apparent oscillation of the sun leading to analemma is a result of two movements of the earth . If the orbit of the earth were an exact circle and the earth's axis were perpendicular to the plane of the orbit , then the sun would always be at the same point in the sky at the same moment of an evenly running time (also not at different heights, because there would also be no seasons). However, the orbit of the earth is elliptical and the deviation of the apparent orbit plane of the sun, also known as the ecliptic , from the celestial equator (projection of the equator onto the sky) is approx. 23.5 °. As a result, the sun deviates from this point for a year and wanders once through a figure with the shape of an "8", the analemma.
The above photomontage shows the different positions of the sun over the year around 9 o'clock CET at around the 8th east longitude and around 49th north latitude , with the sun covering the lower, wider part of the double loop ("8") from the beginning of September to Clockwise in mid-April, the upper, narrower part from mid-April to early September in the opposite direction. The deviation from the drawn auxiliary straight line is the advance or lag of the true solar time ( true local time (WOZ)) from the artificial mean solar time ("mechanical time", mean local time (MOZ)), expressed using the equation of time . The adjacent graph of the equation of time is stretched in width compared to the above photomontage, the analemma is only contained in it schematically.
The analemma figure only gained general importance through the invention and use of the basically uniformly running mechanical clock at the end of the Middle Ages . In ancient times, the apparent motion of the sun itself was a commonly used measure of time. Their slightly irregular course was accepted or was not known to the general public.
The analemma on sundials
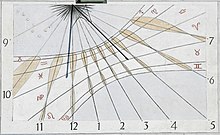
On sundials with point displays, the mean local time (MOZ) can be read on analemma-shaped hour markers. On the wall sundial shown , it is not the stick shadow on the hour lines, but the dot shadow (originating from the ball on the stick tip) on the analemma-shaped hour markers.
The Analemma of Vitruvius

In the ninth of his ten books on architecture , Vitruvius suggests how sundials can be constructed using a figure he calls analemma. He describes how to draw the analemma using just a ruler and compass. His example applies to Rome, it begins with the ratio of shadow length to gnomon height, as it is valid there at the equinoxes. The gnomon point is in the center A of the circle, which represents the meridian of the location. From the tangent of the latitude of Rome, i.e. H. The equator and thus the course of the sun ray NAC at the highest point of the sun at noon can be plotted from the equinox length ratio of shadow to gnomon (8: 9; CB: AB). Parallel secants LG and KH to the equator at a distance of 1/15 circumference approximate the respective orbital planes of the sun to the solstices (declination of the sun ± 24 °). At the winter solstice, the sun is projected from K via A to T. At the summer solstice, it is mapped from L to A to R. In the selected view the sun moves up and down on these solstice secants between horizon EI and midday points L and K once a day. Thus, the intersections S and V of these orbits with the horizon are the constellations at sunrise and sunset. The corresponding time to the day's position of the sun can be determined if a (semicircle) circle is drawn around the respective secant of the sun's path , which is divided into hour angles of 15 ° each. Vitruvius no longer describes the subdivision. In the figure on the right, the time reading for sunrise and sunset on the day of the summer solstice is shown by the line S - SA-SU. For the declination range between summer and winter solstice, the Menaeus described by Vitruvius, the monthly or zodiac can be subdivided. The position corresponding to the desired calendar day of a month is plotted on this and a parallel to the equator is drawn through this point. This gives the secant of the sun's orbit for that day. Their upper intersection with the meridian circle results in the projection beam for the midday sun. In order to be able to determine the position of the sun during the daytime hours, a semicircle with a corresponding division of the hours is drawn around this secant.
See also
literature
- Georg Kauffmann: Analemma . In: Paulys Realencyclopadie der classischen Antiquity Science (RE). Volume I / 2, Stuttgart 1893ff., Sp. 2052-2055.