Gnomon


The gnomon (from Greek γνώμων gnomon shadow pointer ) is an astronomical instrument known even before antiquity in the form of a wooden stick stuck vertically into the ground. The development went from the wooden stick as a shadow pointer to the occasional relevant use of an obelisk . The tip of the sun's shadow is observed to determine astronomical magnitudes.
He served u. a. as a shadow stick for sundials . Based on this early use, the doctrine of the sundials is called gnomonic , and the central projection of a spherical surface (e.g. the celestial sphere in which the sun is located) through its center (represented e.g. by a gnomon tip) is called a gnomonic Called projection .
Application of the gnomon
In ancient times, the gnomon was used to determine the latitude of a place, the north direction , the equinoxes ( equinoxes ), the solstices ( solstices ) and the ecliptic . For this purpose, the gnomon was usually designed as a simple staff (mostly made of wood), rarely as an obelisk or as a special structure. What all gnomons have in common is the special design of the tip: so that their shadow is sharply depicted and thus precisely readable, it is pointed or provided with a small ball (nodus). A variant with a perforated disc at the tip to create a light spot is already known from ancient China.
A central projection of the celestial sphere on a plane is named after the gnomon , the gnomonic projection . With it, the shadow point of the mode can be calculated for every location and position of the sun and a two-dimensional network of curves can be constructed on the dial. On the lines, which are all conic sections , both the time of day and the season can be read.
Story of the gnomon
At the beginning, probably only the length of the shadow was read and interpreted by the gnomon, who could be humans themselves. An astronomical instrument with a gnomon could have been a noon wise man . The midday shadow length was measured with the help of a scale placed on the floor in the meridian direction.
Little is known about this very early step in various cultures (including ancient China). On a Babylonian clay tablet from around 2300 BC Chr. The shadow lengths of a gnomon are given at different times.
The gnomon is said to have been an important astronomical instrument for the Chinese from the earliest times. In one of the oldest mathematics books , the Zhoubi suanjing , the eleventh century BC Living Duke of Zhou, Zhou Gong Dan, his court official Shang Gao performed mathematical tasks, including converting the length of the shadow of the gnomon into the position of the sun. Chinese astronomers used and further developed the gnomon at least until the early Yuan Dynasty (see Gaocheng Observatory ). According to Herodotus (approx. 485–425 BC) the Greeks adopted the principle of the gnomon from the Babylonians.
By equipping a noon sign with an hour scale, it finally became a full-fledged sundial. There are texts and finds of sundials from ancient Egypt . However, the ancient Egyptian shadow clock and a wall sundial used at the same time were not suitable for correctly displaying the hours of the day in every season. Both clocks used a horizontal shadow projector, one edge one, one rod the other. This type of sundial was used again in the Middle Ages (see canonical sundial ). From sundials from the fourth century BC. BC in Greece Vitruv reports (see main article Sundial ).
Eratosthenes of Cyrene presented 225 BC. He took measurements with gnomons, from which he calculated the circumference of the earth to be about 252,000 stages. He found that the midday height of the sun in Alexandria differs from that in Syene (Aswan) by about 7.2 °. With this angle and the known distance of about 5,000 stadiums between the two cities, which are fairly on the same longitude, he obtained a result that comes very close to the actual value of 40,024 kilometers (about 240,000 stadiums).
Mathematical basics for using the gnomon
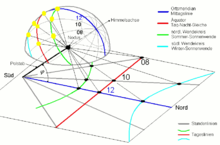
Projection of the sun onto a clock face
The image of the sun through a point is a central projection. Because of its development in connection with gnomonic, it is also called gnomonic projection . The projection center is in the center of the sky (equal to the center of the earth). The simplification of moving the center of projection onto the surface of the earth in the tip of a gnomon is permissible for the task, since the sun is so far away that the parallax is negligible due to the earth's radius. The figure [3] shows a gnomonic projection with a vertical gnomon and a horizontal projection surface, which is, for example, the surface of the dial of a sundial (horizontal sundial). All great circles such as the celestial equator and the meridian running through the location are shown as straight lines in the gnomonic projection. Since the hour circles of the sun are also great circles, they are shown on the dial as a straight line (hour line) that converges at the point of intersection of the polar axis on the projection surface. The tropics are shown as hyperbolas . This shows that the shadow of the gnomon peak at the equinox runs from sunrise to sunset on a straight line and intersects the straight line of the hour. At the solstice it moves on a hyperbola and also intersects the hour lines over the course of the day.
Figure [3] shows that the shadow of the vertical gnomon staff intersects the straight hour line. If the rod were to be placed on the projection surface at the point of intersection of the polar axis and pointed in the direction of the celestial pole, its shadow, like the straight hourly straight line, would run radially outwards from the point of intersection. Thus every point of the shadow would correctly tell the time. Such a rod is called a pole rod . It depicts the sun in one dimension.
Measurements with the gnomon
Determination of north direction
In order to be able to determine the north direction, it is first necessary to find the point in time when the sun is at its highest point. For this one makes use of the fact that its course in the sky is symmetrical around this point. On the horizontal surface to which the gnomon is perpendicular, a circle is drawn, the center of which is the shadow stick itself. The radius is chosen so that it corresponds to the length of the shadow at the first measurement time in the morning. During the course of the day, the shadow length in the afternoon exactly matches the radius exactly one more time, as can be seen in Figure [4]. If you connect the two points of intersection with the center point and draw the bisector of the resulting vertex, you can see that it marks the direction of the shadow at the highest point of the sun. Since the sun is at its highest point in the south north of the Tropic of Capricorn, the bisecting line that lies exactly opposite it marks the north direction. South of the tropic, however, the bisector is the south direction, as the sun is in the north when viewed from there. If you are between the tropics, it depends on the time of year whether the shadow falls to the north or south at noon.
Determination of the angle of incidence of the sun
If the height of the gnomon and the length of the shadow it casts on the horizontal surface are known, the elevation angle of the sun can be determined using trigonometry :
This is possible because the gnomon forms a right-angled triangle together with the surface to which it is perpendicular , as well as an incident sunbeam, which represents the hypotenuse .
Use of the term in geometry
In mathematics, especially in planar geometry, the term gnomon describes the remaining area between two similar figures. This construction was already known in Greek-Hellenistic mathematics and referred to a geometric figure that is created when a parallelogram is cut out from a parallelogram that is similar and located in such a way that it shares a corner with the original parallelogram.
Sometimes the two complementary parallelograms of the same area of such a construction are also referred to as gnomon. They arise when straight lines are drawn through a point on the diagonal that are parallel to the sides of the parallelogram (see Gnomon's theorem ).
Gnomon metaphor in biblical exegesis literature
In theological literature, the term gnomon was used figuratively as a metaphor in a famous work of biblical exegesis .
In 1742, the pietistic theologian Johann Albrecht Bengel (1687–1752) published the Latin Gnomon Novi Testamenti , a commentary on the New Testament that strived for accuracy and was supposed to reveal the true meaning of the text . With this emblematic (symbolic) choice of the term "pointer" Bengel points to his interest in what he believes is a chronologically comprehensible, calculable history of salvation , which, according to the statements of the St. John Apocalypse that he deciphered, should run like clockwork . Bengel's son-in-law Philipp David Burk also used the term in his exegesis of the Psalms.
literature
- Oskar Becker : The mathematical thinking of antiquity. 2nd Edition. With an addendum by Günther Patzig . Vandenhoeck & Ruprecht, Göttingen 1966, ISBN 3-525-25304-4 ( Study books on Classical Studies 3).
- François Dom Bedos di Celles : La Gnomonique pratique, ou l'art de tracer les cadrans solaires. Avec des observations sur la maniere de regler les Hozloges. Chez Briasson, Despilly, Hardy, Paris 1760. Facsimile edition: Laget, Librairie Paris 1978, ISBN 2-85204-076-X .
- Dieter Lelgemann , Eberhard Knobloch , Andreas Fuls, Andreas Kleineberg: About the ancient astro-geodetic measuring instrument Skiotherikós Gnomon. In: ZfV. Journal of geodesy, geoinformation and land management. 130, No. 4, 2005, ISSN 1618-8950 , pp. 238-247.
- Helmut Minow: shadow measurement with the gnomon. In: ZfV. Journal of geodesy, geoinformation and land management. 130, No. 4, 2005, pp. 248-252.
- René RJ Rohr: The sundial. History, theory, function. Callwey, Munich 1982, ISBN 3-7667-0610-1 .
- Karlheinz Schaldach, Roman sundials. An introduction to ancient gnomonic. 3. Edition. German, Frankfurt am Main 2001, ISBN 3-8171-1649-7 .
- Karl Schoy : About the gnomon's shadow and the shadow tables of Arabic astronomy. A contribution to Arabic trigonometry based on unedited Arabic manuscripts. Lafaire, Hanover 1923.
- Vitruvius: Vitruvii De architectura libri decem. = Ten books on architecture. Translated and annotated by Curt Fensterbusch. License issue. 5th edition. Primus, Darmstadt 1996, ISBN 3-89678-005-0 .
Individual evidence
- ↑ René RJ Rohr: The sundial. History, theory, function . Callwey, Munich 1982, ISBN 3-7667-0610-1 , p. 10.
- ↑ René RJ Rohr: The sundial. History, theory, function . Callwey, Munich 1982, ISBN 3-7667-0610-1 , p. 13.
- ↑ The new Brockhaus , Volume 2, p. 399, Wiesbaden 1959.
- ↑ See Reinhard Breymayer : "Gnomon typusque vitae Christianae". On the emblematic background of the "gnomon" term in Heinrich Oraeus (1584–1646) and Johann Albrecht Bengel (1687–1752) ". In: Blätter für Württembergische Kirchengeschichte , vol. 88 (1988). Festschrift for Gerhard Schäfer . Ed. by Martin Brecht, Stuttgart [1989], pp. 289-323.