Eratosthenes
Eratosthenes of Cyrene ( ancient Greek Ἐρατοσθένης Eratosthénēs ; * between 276 and 273 BC in Cyrene ; † around 194 BC in Alexandria ) was an extraordinarily versatile Greek scholar in the heyday of Hellenistic science.
He worked as a mathematician, geographer, astronomer , historian, philologist , philosopher and poet. On behalf of the Egyptian kings from the Ptolemaic dynasty , he headed the library of Alexandria , the most important library of antiquity , for around half a century . With its excellent facilities, the library offered him excellent working conditions. He is particularly famous as the founder of scientific geography. His determination of the circumference of the earth based on careful measurements is one of the most famous scientific achievements of antiquity. In addition to his research work, collecting and organizing existing knowledge was one of his main concerns. Of his numerous lost works, only a tiny fraction is known from quotes and reports by later authors, which makes it very difficult to appreciate his life's work.
As the first ancient scholar, Eratosthenes called himself a "philologist". By philology he understood not only preoccupation with linguistics and literary studies, but in a more general sense a versatile scholarship. His criticism of the poets, which even a high-ranking authority like Homer did not spare, is characteristic of his impartial attitude towards ingrained convictions . He did not approve of any truthfulness to the descriptions of the poets, since their aim was only entertainment and not instruction.
Life
Eratosthenes came from the city of Cyrene in what is now Libya . His birth can be traced back to the period between 276 and 273 BC. Limit Chr. He went to Athens to study . His teachers were the grammarian Lysanias of Cyrene , the stoic philosopher Ariston of Chios and the Platonist Arkesilaos . Ariston, who was only interested in ethics and considered scientific studies to be unimportant, does not seem to have had any lasting influence on Eratosthenes. The impressions that Eratosthenes received from the thinkers of the Platonic Academy were evidently far stronger , for his later statements on philosophical subjects show him to be a Platonist . However, he does not seem to have been a regular member of the academy. In addition, the famous scholar Callimachus of Cyrene is also mentioned as the teacher of Eratosthenes in the ancient tradition , but this information is hardly credible. Other philosophers who impressed Eratosthenes were Arkesilaos' disciple Apelles of Chios and the Cynic Bion of Borysthenes . An unclear and controversial, chronologically problematic remark by Strabons about a relationship between Eratosthenes and the Stoic Zeno von Kition need not be interpreted in terms of a teacher-student relationship.
The Egyptian king Ptolemy III brought him from Athens . Soon after taking office, probably around 245, Euergetes moved Eratosthenes, who was only about thirty, to his residence city of Alexandria. Apparently the young scholar already enjoyed an excellent reputation at that time, with his poetic and mathematical-philosophical achievements in the foreground; his geographical, philological and historical works came about later. The king appointed him head of the library of Alexandria after his predecessor in this office, Apollonios of Rhodes , because of differences of opinion with Ptolemy III. had resigned. From about the middle of the thirties Eratosthenes taught the son and future successor of the king, Ptolemy IV Philopator , who ascended the throne in 222.
There is no reliable information about the later life of Eratosthenes. He kept the library manager until the end of his life. Various information are available about his death. The Suda , a Byzantine encyclopedia, reports that he himself ended his life by refusing to eat because of blindness. Such a death was then considered worthy of a philosopher. The poet Dionysius of Kyzikos, on the other hand, who wrote a poem on the deceased shortly after the death of Eratosthenes - probably as a grave inscription ( epitaph ) - wrote: “Very mild old age wiped you out, not a debilitating disease”. Dionysius therefore assumed the old age of the eighty year old as the cause of death; maybe he wanted to counter the rumor that it was suicide. Eratosthenes was buried in Alexandria.
Despite his fame and extraordinary erudition, Eratosthenes did not found his own school. Of the four people named as his students in the Suda, three are not clearly identifiable, so they were hardly important scientists. The fourth is the prominent grammarian Aristophanes of Byzantium , who succeeded Eratosthenes as head of the library in Alexandria.
Works and achievements
Eratosthenes wrote numerous works, of which only fragments have survived. His views and achievements are therefore only known from these fragments and other information in ancient literature. There are roughly three phases in his mental development. In the first phase he dealt intensively with philosophy (especially Platonism), in the second the natural sciences came to the fore, in the third his focus shifted to philology. The constant of his work were the preoccupation with technical problems and the special attention to cultural-historical aspects of his research areas.
astronomy
Fonts
Three astronomical writings by Eratosthenes are known, but only survived in fragments:
- The star book cited in the Suda with the title Astronomy or Cadastre . The original title was probably On the Order of the Stars and the Origin of the Celestial Signs . The star book contained a star catalog with brightness information for individual stars. However, it served not only an astronomical but also a mythographic purpose, because it also comprised a collection of legends relating to individual stars and constellations. From this work, which has not survived, a modified version was made in the 2nd century AD, the cadastral system , which was then distributed under the name of Eratosthenes. This new version is also not preserved in its original form, but can be reconstructed from a surviving extract ( epitome ) as well as information in Hygin and in Scholien on Aratos by Soloi and Germanicus . The Katasterismen treated - as already the original work - Myths about 44 constellations and celestial bodies, and the five known planets and the Milky Way were counted than any constellation.
- The paper On Measuring the Earth , which dealt with a number of astronomical and geographical subjects. This included determining the circumference of the earth and measuring the inclination of the ecliptic , the size of the moon and sun and their distance from the earth, the differences in the length of the day depending on the latitude and the season, the distances between the tropics and the polar circles and questions about the total and partial solar and lunar eclipses . Another subject was the winds; Eratosthenes is said to have introduced a compass rose . A supposedly ancient script in which the invention of an equally divided eight-line compass rose is attributed to him is a forgery from the Renaissance period . In the case of the late antique author Oreibasios , however, information can be found that may indicate an authentic wind rose by Eratosthenes.
- About the eight-year cycle , an investigation into the calendar calculation, which concerned the determination of the relationship between the solar and lunar years and a special problem of the solar year. It had been found that a cycle of eight calendar years (octaeteris), namely five normal years of twelve months and three leap years of thirteen months, corresponded to about eight solar years, so that after eight years the sun and moon again approximately have the same positions with regard to the equinoxes and solstices revenue. This inaccurate calendar calculation - the error was a day and a half per cycle - was the general subject of the investigation. The starting point for the special discussions of Eratosthenes was the problem that a festival of the goddess Isis fell back one day every four years due to the lack of leap days and thus wandered backwards through the year over the centuries. Presumably Eratosthenes suggested solving the problem by adding a leap day. In 238 Ptolemy III ordered. introduced a calendar reform with which a leap day was inserted every four years. The assumption that this happened on the recommendation of Eratosthenes is obvious. The reform, which anticipated the principle of the Julian calendar , did not take hold in the long term.
Determination of the circumference of the earth
The spherical shape of the earth was known to the Greeks long before Eratosthenes. Aristotle already dealt with the question of their scope. He cited "mathematicians" who were not named and who had determined a range of 400,000 stages , a number that was probably more estimated than calculated. The exact length of the stadium length used by the “mathematicians” is unclear, so different numbers are given when converting to kilometers. A few decades later (after 309 BC) a researcher - possibly Dikaiarchos - determined a circumference of 300,000 stages. Eratosthenes is the only scholar of antiquity for whom a scientifically sound measurement is attested. The prerequisites for this were excellent: he had excellent knowledge of both mathematics and geography, had access to the relevant literature in the library and could rely on the support of the king to carry out the complex measurements. The result was 250,000 stadiums; later he changed it to 252,000.
The method of Eratosthenes is handed down in a summarizing and simplifying description of the imperial astronomer Cleomedes . If you follow this description, it consisted of the following steps: He assumed that the Egyptian cities of Alexandria (on the Mediterranean coast) and Syene (today's Aswan , the southernmost city of the country ) lie on the same meridian (degree of longitude). The distance between two measuring points established by Eratosthenes in the two cities was, as far as he knew, 5000 stages. Since Alexandria was only founded in the 4th century, he could not rely on information in ancient Egyptian literature for the distance, but probably had the distance between his two measuring points precisely measured by royal pedometers. At both locations he set up a gnomon , a metal hemisphere with graduations on the inside with a vertical pointer to read off the shadow that is created. The measurement of the height of the sun above the horizon was carried out with these devices at noon on the day of the summer solstice . It showed that the shadow pointer in Syene cast no shadow, so the sun was right there at the zenith . In Alexandria, the sun was at this point in time the "fiftieth part" of a full circle from the zenith, ie 7 ° 12 ′ according to today's circular division into 360 degrees . Thus one had to migrate 5000 stadiums south to cover one fiftieth of the circumference of the earth. This resulted in a value of 50 × 5000 = 250,000 stages for the circumference of the earth.
A considerable inaccuracy results from the fact that Alexandria and Syene are not actually on the same meridian; Syene is located about 3 ° east of Alexandria. Since a value of 5000 stadia was measured for the distance between the two cities , a distance of 4615 stadiums would have resulted for a point lying exactly on the meridian arc of Alexandria and thus an amount of 50 × 4615 = 230,750 stadiums for the circumference of the earth. The error as a result is 7.7%.
It is unclear how long the "stadium" measure used for the measurement was. It can hardly be about the 185-meter-long “Olympic” stadium, because then the pedometers would have been wrong by several day trips when determining the distance between the two cities, which is actually 835 km as the crow flies. Therefore, numerous researchers assume that the length measure used was significantly shorter. The assumptions vary between 148.8 and 180 meters. A particularly often mentioned number, which is derived from a statement in the Naturalis historia Pliny the Elder , is 157.5 m. Assuming the actual distance of 835 km, the result for the stadium is 835,000 m: 5000 = 167 m.
For the accuracy of the determination of the circumference of the earth, the unit of length used does not play a role: According to the experimental concept and the measurement, it is fifty times the distance from Alexandria to Aswan, according to today's units it is 835 km by 50 equal to 41,750 km, which is the actual distance Value (40,075 km at the equator) comes very close. The error is around 4.2%.
Two inaccuracies in the assumptions on which the calculation is based are negligible:
- Eratosthenes believed that the rays hitting different parts of the earth from different parts of the sun are parallel. This was an essential prerequisite for his experiment, because the difference in the angle of incidence of the sun only corresponds to the difference in latitude between the two places if the sun is so far away from the earth that the rays emanating from it strike almost parallel to different places on earth. This is not exactly the case, but this fact can be neglected, since the deviation is only about one arc second .
- Syene was not, as Eratosthenes believed, exactly on the tropic, where the sun reached its zenith on the day of its turning, but at that time about half a degree north of it, but this difference only slightly affected the measurement result.
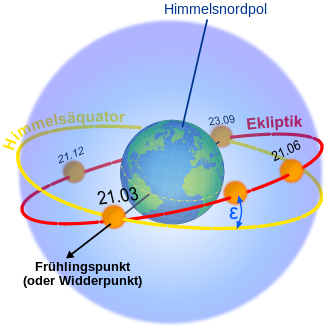
Obliqueness of the ecliptic
Eratosthenes determined the inclination of the ecliptic . The ecliptic is the apparent circular path of the sun projected onto the imaginary celestial sphere over the course of a year; their inclination is the inclination of their plane with respect to the plane of the equator. The value of this angle (ε) is not constant; at the time of Eratosthenes it was 23 ° 43 '40' '. As early as the 5th century BC . BC was Oenopides come from Chios to 24 °; Eratosthenes improved the measurement accuracy. He determined the angular distance between the two turning circles of the full circle (360 °), i.e. 47 ° 42 '40' ', which results in a value of 23 ° 51' 20 '' for ε by halving it. How he came to this result is unknown; the hypotheses considered in research are speculative.
geography
Eratosthenes wrote only one geographical script, geography (Geōgraphiká) in three books. This script, which was regarded as a standard work throughout antiquity, has only survived in fragments. It was the most famous and influential of his works as scientific geography began with it. Presumably it was he who coined this previously not attested term. For him, geography literally meant "drawing (gráphein) the earth", by which he meant, in addition to merely describing the surface of the earth, mapping, measuring, dividing and localizing. In doing so, he built on the findings that he had already presented in the treatise On Measuring the Earth , which treated geography from an astronomical point of view.
First he described the basics of geography including its history. In his analysis of the views of earlier naturalists, he only accepted the mathematical-physical approaches and rejected the claims of the poets. He insinuated that the poets were only aimed at entertainment and not at instruction. Therefore, he thought their geographic information was worthless. This criticism was directed particularly against the authority of Homer , who was ignorant of the geographical conditions outside of Greece.
Then Eratosthenes put forward his own views. Apparently he was explaining the geographical consequences of the findings presented in his treatise on geographic surveying. He probably presented all known evidence for the spherical shape of the earth and discussed the distribution of water and land on the earth's surface. Thanks to geological observations, it was clear to him that the relationship between water and land is not constant; from finds of fossilized mussel shells he concluded that the Libyan desert was once a sea. He shared the idea, already widespread at the time of the pre-Socratics , that the Oikumene (the well-known, populated part of the earth's surface) was a huge island surrounded by the ocean. From this he concluded that, in theory, one could get from the Iberian Peninsula across the Atlantic to India by sea if the size of the ocean allowed such a journey. He tried to determine the length and breadth of the island. For the maximum length it came to 77,800 stadiums by adding known or estimated route sections, for the maximum width to 38,000 stadiums. He designed a coordinate system with meridians and parallel circles that provided the basis for his map of the inhabited world, which he presented and explained in the third book.
He drew his knowledge of distant countries from the travel reports that were available to him. He viewed their often inaccurate or erroneous information critically in order to then evaluate them for his cartographic project, insofar as they seemed credible and coherent to him. His position as head of the extraordinarily well-stocked library of Alexandria - the best in the ancient world - gave him the unique opportunity to use the wealth of information of the seafaring and country descriptions available at the time.
He divided the Oikumene by the diaphragm , a parallel to the equator that ran through the columns of Heracles , into a north and a south part. With that he gave up the traditional division into three continents. In the further division he distinguished at least four large country complexes , which he called "seals" ( sphragídes , plinthía ). He saw Africa as a right triangle. He was less well informed about southwest Europe than about the Orient, about which relatively detailed information had been available since the campaigns of Alexander the Great and the Diadochi . For the north-west he relied on the travelogue of Pytheas , which ancient critics resented, because Pytheas was not considered credible. He cited the Carthaginians' xenophobia as the cause of the lack of reliable reports on the West . His knowledge of the north and northeast was inadequate; he considered the Caspian Sea to be a bay of the northern world ocean. He did not limit his description of the earth to topographical facts, but included cultural and economic geography as well as historical and political conditions.
Mathematics, music theory and metaphysics
The philosopher and mathematician Theon von Smyrna quotes two passages from a work by Eratosthenes entitled Platōnikós , which has not survived . To which literary genre the Platonikos belonged is controversial. Some scholars have thought of a comment on Plato's dialogue Timaeus , but Eratosthenes does not seem to have limited himself to a discussion of just one single work of Plato. It was often assumed that it was a question of a dialogue in which Plato appeared as the main speaker, but then, according to ancient custom, the script should be called Plato and not Platonikos . Platonikos is probably to be understood in the sense of Platonikos logos (writing about Plato) . It was probably a handbook that was supposed to make Plato's works easier for a wider audience by clarifying terms and explaining difficult passages.
Mathematical questions were primarily dealt with; Terms discussed included distance, ratio, continuous and discontinuous proportion, mathematical mean, prime, and point. The focus was on the doctrine of proportions, in which Eratosthenes saw the key to Platonic philosophy. For him, mathematical knowledge also meant philosophical knowledge. The aid of the ratio equation (“a relates to b as c to d”), which he called “analogy”, should also help to gain extra-mathematical knowledge. He generally strived for problem solutions by looking for analogies in the sense of proportional equations. In proportion he thought he had found the connecting link between the "mathematical" sciences (arithmetic, geometry, astronomy, music theory), since all statements made by these sciences can ultimately be traced back to statements about proportions.
Just as one is the starting point (archḗ) and the original element (stoicheíon) of numbers and thus of quantity and like the point is the indissoluble, non-traceable element of length, for Eratosthenes equality (as an original ratio 1: 1) is that Element and the origin of all ratios and proportions. The numbers arise through addition and the various ratios through enlargement of the terms of the initial ratio; the line, on the other hand, cannot be produced as a joining together of individual points, since the individual point has no extension, but rather it arises from a continuous movement of a point. This view was later criticized by the skeptic Sextus Empiricus .
For the problem of doubling the cube , the "Delic problem", which cannot be solved with a compass and ruler , Eratosthenes proposed an approximate mathematical solution. For research on prime numbers, he used an algorithm that made it possible to remove all prime numbers from the set of all odd natural numbers that are less than or equal to a given number. This method is known as the sieve of Eratosthenes . But he did not invent it - as was previously believed; Rather, it was already known, only the name "sieve" comes from him.
A secondary theme of Platonikos was music theory, in which Eratosthenes transferred the theory of proportions to music. He succeeded so convincingly that in ancient times he was counted among the most important authorities in the musical field. The scholar Ptolemy passed on the calculations of Eratosthenes for the tetrachord , which show that he used the "Pythagorean" attunement, which he refined. Eratosthenes knew and also took into account the system of the music theorist Aristoxenus . How he proceeded with his calculations, however, does not tell Ptolemy.
Furthermore, Eratosthenes also went into the metaphysical such as the theory of the soul in Platonikos . Like the Platonist Krantor , by whom he was probably influenced, he took the view that the soul cannot be purely immaterial, but must also have something corporeal about it, because it resides in the world of sensually perceptible things; besides, it is always in a body. This is based on the idea that the soul can only grasp sensually perceptible objects if it has a corresponding disposition in its own structure. According to this, it is a mixture of two components, one incorporeal and one corporeal.
The late antique mathematician Pappos mentions a mathematical text by Eratosthenes with the title About middle limbs (Peri mesotḗtōn) . Since this work is not mentioned anywhere else in ancient sources, it can be assumed that it is identical to Platonikos . In 1981 a medieval Arabic translation of a text by "Aristanes" (Eratosthenes) about medium proportions was published. This is not, however, about the lost work On Mittelglieder mentioned by Pappos , but an alleged letter from Eratosthenes to King Ptolemy III, also preserved in the original Greek text. about doubling the cube. The authenticity of the letter is disputed.
Smaller philosophical writings
In addition to Platonikos , Eratosthenes wrote a number of smaller philosophical works, some in dialogue form, of which only the titles and some isolated quotations have survived:
- Arsinoë , apparently a dialogue; Only a single fragment handed down from Athenaios is preserved. The eponymous figure is probably the Egyptian Queen Arsinoë II , not - as was previously believed - Arsinoë III. In the fragment, the queen makes derogatory comments about an Egyptian festival.
- Ariston , a dialogue explicitly mentioned only in Athenaios, which probably dealt with the doctrine of virtue of the Stoic Ariston, who was Eratosthenes' teacher. In the dialogue it is reported that Ariston was caught when he "broke through the wall between pleasure and virtue and appeared on the side of pleasure", that is to say, when he failed to comply with philosophical asceticism .
- About wealth and poverty , probably a dialogue known from a mention by the doxographer Diogenes Laertios .
- On Wealth , a multi-volume work that Plutarch mentions.
- About Painlessness , an apparently popular work mentioned in the Suda, presumably in dialogue form.
- To baton , probably a dialogue; a fragment has come down to us from Diogenes Laertios.
- On good and bad , a treatise on ethics from which four smaller fragments have been preserved. It contained biographical material that illustrated statements about virtue and wickedness. In this context, there was talk of the deaths of prominent personalities and of philosophical steadfastness. Another topic was Alexander the Great's personnel policy , in which Eratosthenes praised the fact that the king valued and promoted virtuous men regardless of their origin, instead of relying only on Greeks and treating the “barbarians” as subjugated enemies. In doing so, Eratosthenes criticized the widespread notion of a natural difference in rank between Greeks and non-Greeks, of which Aristotle was one of the representatives.
- About schools in philosophy , a doxographic, philosophical-historical work mentioned only in the Suda. If the indication of the Suda is correct, it is the oldest known script of this type.
Historical works
According to the Suda, Eratosthenes wrote historical works (historíai) . Only one work known by name can possibly be assigned to him: the story of the Galatians (Galatiká) . Only sparse fragments have survived. This work is usually denied Eratosthenes, but his authorship cannot be ruled out. Since it cannot have been written before 205, if he is the author, it should be an old work.
Eratosthenes is considered the first chronograph and founder of scientific chronography (creation of a time frame in which historical events are classified). His interest, however, was apparently directed more towards the gathering of culturally and historically interesting news than the determination of an absolute chronology. Therefore, its role in this area is not as prominent as it was often assumed in older research. Three relevant writings of his are mentioned in the sources:
- The kings of the Thebans , a list of the Egyptian rulers of Thebes , which he is said to have translated from Egyptian into Greek on a royal commission . Such a list has been preserved, but cannot come from him in the present version. To what extent it contains material that can be traced back to him is unclear.
- About chronographs , a treatise on the division of epochs from which fragments have been preserved. Eratosthenes dealt with older approaches. He began with the conquest of Troy , which he considered to be a historic event. He did not consider the earlier, because he did not trust the tradition because of its fabulous character. Here, too, his critical, scientific way of thinking is evident. He came to the conclusion that there were 860 years between the conquest of Troy and the death of Alexander the Great. He divided this period into ten "epochs" of different lengths, which he started and ended with striking military, cultural, historical or political events. He calculated the distances between these fixed points on the basis of chronological information provided by historians. He does not seem to have used an absolute temporal framework.
- Olympiaieger (Olympioníkai) , a multi-volume work known from quotations in later literature about the winners in the Olympic Games and the history of sport with special consideration of the chronology. The counting of the Olympiads for the purpose of dating events was introduced by Timaeus of Tauromenion and served as a framework for calculating time even before the time of Eratosthenes. Eratosthenes evaluated the literature available to him; he did not use inscribed sources. His work was also a collection of cultural and historical information.
poetry
While Eratosthenes is only famous today as a scientist, in ancient times he was also valued as a poet and even compared to the poet Archilochus . He was recognized in the field for the elegance and formal flawlessness of his verses, but was chalked up for a certain lack of inspiration. Six poems are mentioned in the sources:
- Erigone , an elegy in Ionic dialect famous in antiquity for its formal perfection , from which only a few verses have survived. The fate of the Athenian Erigone , the daughter of the farmer Ikarios , a mythical figure is depicted. Ikarios receives the order from the god Dionysus to spread the previously unknown viticulture. Ikarios is murdered by farmers who consider the wine to be a poison because of its novel intoxicating effects. Desperate about it, Erigone hangs herself. Her dog Maira is waiting with the dead until she dies herself. Later, Ikarios, Erigone and Maira are transferred under the stars by the gods. Famous is a verse of the Erigone , much discussed in ancient and modern times, which speaks of the introduction of a dance that was danced for the first time after Ikarios had killed a goat (Greek trágos ) that had invaded his vineyard. This dance is associated with the emergence of the tragedy as “goatsong”. The verse has been handed down incorrectly, its wording and its interpretation are controversial.
- Hermes , an extensive epic poem shaped by the natural philosophy of Plato, which described the actions and experiences of Hermes , the messenger of the gods , and comprised around 1,600 verses. At least 19 fragments have survived from it, but there is no clear picture of the structure and content. The poet used the motif of Hermes' ascent to the heavenly spheres to portray a cosmological subject that was familiar to him as an astronomer and Platonist: He described the structure of the universe and especially the Pythagorean- Platonic concept of the harmony of the spheres . This gave the Hermes the character of a scientifically oriented didactic poem. Hermes, the inventor of the lyre , ascends to the sky, walking through the eight celestial spheres from the moon to the fixed stars. He is amazed to see that the spheres produce tones that correspond to those of the instrument he has created. A tone is assigned to each of the eight spheres, resulting in a scale with an octave range. The motionless earth in the center of the cosmos does not produce any sound.
- Hesiod or Anterinys , a purely hexametric poem from which few fragments have survived . The subject is an act of revenge. The famous poet Hesiod is suspected of seducing a woman who hanged herself after being dishonored. Their brothers kill Hesiod, throw his body into the sea and flee. They are later exposed and executed by the barking of the murdered man's dog. It turns out that Hesiod was innocent of the crime he was accused of.
- Dionysus with the open mouth , a poem about the mythical Samian Elpis, who first flees from a lion, but then comes to the aid of the predator. The grateful lion then shares its prey with humans.
- A wedding song that has not been preserved ( Epithalamion ).
- The " dedication epigram ", the only completely preserved poem by Eratosthenes. It was to King Ptolemy III. directed and accompanied a device later called "Mesolabos", which Eratosthenes had constructed for the king. The instrument worked mechanically on the principle of the slide rule . It consisted of a rectangular frame containing small plates that could move in grooves. The mesolab was used to mechanically determine the two mean proportions of two given distances and thus to double the cube mechanically.
philology
In addition to his geographical work, Eratosthenes' philological work received the most attention in antiquity. But they have only survived in (relatively numerous) fragments. He was considered an authority in this field and was the first ancient scholar to call himself a "philologist", which meant not just philology in the modern sense, but also learning in general. His extensive main philological work was entitled About the Old Comedy . In it he discussed questions of textual criticism , the authorship of individual pieces, the performance time and performance practice and explained historical backgrounds. First and foremost, he dealt with linguistic phenomena, with the investigation of individual words and expressions and dialectal peculiarities that provided him with criteria for clarifying questions of authenticity and ascription. He dealt critically and sometimes sharply with the views of earlier authors. The old comedy became a standard work.
Another font was entitled Grammatiká (grammatical) . He also wrote a treatise on terms from the world of handicrafts, the Architektonikós (craftsmanship) , and one on the names of household appliances, the Skeuographikós (equipment) , as well as a commentary on Homer's Iliad from a special, not traditional point of view. According to the Suda, his grammatical works were numerous.
Eratosthenes also wrote letters in which he responded to philological and cultural-historical questions. Two fragments are preserved.
reception
Antiquity
The famous mathematician Archimedes was in correspondence with Eratosthenes. He honored him by dedicating his writing Methodology to him, his only work on methodology . There he described him as an excellent scholar, emphasizing his philosophical merits and at the same time suggesting that he considered the mathematical achievements to be less important. Archimedes also apparently sent Eratosthenes the 22 distich poem Das Rinderproblem about a difficult mathematical problem that he wanted to present to the mathematicians in Alexandria; however, the authenticity of the verses is not certain.
The versatility of Eratosthenes struck contemporaries and posterity, but it was not only rated positively. Critics felt that he distinguished himself more for his breadth of interests and erudition than his depth of understanding or pioneering achievements in any particular field. This assessment was also expressed in his nicknames or surnames, which were probably already widespread in his environment during his lifetime; the people of Alexandria were famous for their ridicule. With his opponents he was considered a "know-it-all" (as opposed to a real philosopher). In this sense they called him “ pentathlete ” (Péntathlos) - someone who achieves remarkable achievements in several areas, but is not the best in any of the individual disciplines. The nickname Beta - "the second" in the sense of "secondary" - was also common. Given this background, it is possible that the designation as “Second Plato” or “New Plato” was not only meant positively, but was also intended to indicate a lack of originality.
Apparently, wide circles only grudgingly paid him tribute. Specialists looked for and found weak points, which they used to sometimes exaggerated criticism. Strabo and Pliny the Elder generally praised his competence in various fields of knowledge, but when it came to specific individual questions, Strabo had a lot to complain about in terms of his expertise and judgment. Polemon von Ilion sharply criticized Eratosthenes , who for this purpose wrote a multi-volume pamphlet on the presence of Eratosthenes in Athens . The preserved fragments show that Polemon accused his opponent of lacking knowledge of the cultural history of Athens. Other Eratosthenes critics were the famous astronomer and geographer Hipparchus of Nicaia and the mathematician Nicomedes . Hipparchus reprimanded the unreliability of the world map, Nicomedes wrote a book on conchoids against Eratosthenes , in which he polemicized against Eratosthenes and presented his inventions (such as the mesolabos) as impractical. Polybius severely accused him of having placed his trust in the Pytheas report, criticized his localization and distance information in the Mediterranean area and defended the division of the Oikumene into three continents, which was abandoned by Eratosthenes. The accusation of plagiarism , which was very popular in antiquity , was also brought against Eratosthenes.
The extent to which unfavorable evaluations by ancient critics, who applied strict standards, were justified despite his undoubtedly significant achievements, is difficult to judge, since little of his works has survived. He liked to polemic, express himself sarcastically and, in turn, was the target of attacks.
In the 2nd century, the geographer Dionysius of Alexandria (Dionysios Periegetes) wrote a didactic poem that offers a description of the world, for which the poet relies on information from Eratosthenes, among other things. The poem received a lot of attention in ancient times, in the medieval Byzantine Empire, and in the early modern period. It is not known whether Dionysius had access to the original text of the Geographika of Eratosthenes or obtained his knowledge from a source of funds.
The poems Hermes and Erigone were famous in ancient times. The aftermath of Hermes was considerable, even with Roman authors. Cicero's Somnium Scipionis was probably inspired by Hermes ; Virgil used Eratosthenes' representation of the five heavenly zones that Hermes perceived during his ascent in his Georgica . A contemporary of Eratosthenes by the name of Timarchus wrote a commentary on Hermes in at least four volumes .
It is unclear whether a pictorial representation of Eratosthenes has survived from antiquity. A fresco was found in the Villa Boscoreale depicting an ancient philosopher who is believed to be Eratosthenes. According to a controversial hypothesis, those around the middle of the 1st century BC The frescoes created by Boscoreale were copies of a cycle of paintings commissioned by Ptolemy III. and are based on contemporary portraits of the people shown. Speculative is a conjecture by Konrad Gaiser , who thinks he can recognize Eratosthenes on a famous mosaic from the 1st century AD, which was found in Torre Annunziata in 1897 and is now in the National Archaeological Museum of Naples . Gaiser believes it is probably a copy of a picture that was made in Alexandria soon after Eratosthenes' death and that decorated either his grave or a room in the Museion.
Modern times
When the Dutch astronomer and mathematician Willebrord Snel van Royen published a new method of determining the circumference of the earth in the 17th century , he chose the title Eratosthenes Batavus (The Dutch Eratosthenes) for his work published in 1617 . His contemporary Claude de Saumaise ( Claudius Salmasius ), an important scholar of antiquity, was celebrated as the Eratosthenes of his time.
In 1822, the year of his doctorate, the philologist Gottfried Bernhardy published the first and to this day only collection of the Eratosthenes fragments aimed at completeness. In the following years and also in the 20th century, research concentrated on individual questions. Bernhardy's youth work, a brilliant achievement at the time, is now completely outdated, but has not been replaced.
From today's perspective, the consistently scientific way of thinking and working of Eratosthenes, which earned him special appreciation in modern times, is particularly striking. His pioneering achievements and his impartiality, conscientiousness and comprehensive education are recognized in the research literature. It is also pointed out, however, that Eratosthenes did not excel in all areas to which he turned; In some of his works he shows himself mainly as a material collected by book scholars.
The asteroid (3251) Eratosthenes and a moon crater are named after Eratosthenes .
A surveying expedition commissioned by Eratosthenes is the subject of Arno Schmidt's story Enthymesis or WIEH
The Förderkreis Vermessungstechnisches Museum awards the Eratosthenes Prize for outstanding work in the field of historical research in surveying , in particular for degree theses and dissertations, as well as the Eratosthenes Prize for outstanding book publications.
Editions and translations
Astronomical, geographical and mythographic
- Hugo Berger (ed.): The geographical fragments of Eratosthenes . Teubner, Leipzig 1880 ( online ).
- Jordi Pàmias, Klaus Geus (Ed.): Eratosthenes: Sternsagen (Catasterismi) . Utopica, Oberhaid 2007, ISBN 978-3-938083-05-5 (text, translation and commentary).
- Jordi Pàmias i Massana, Arnaud Zucker (ed.): Ératosthène de Cyrène: Catastérismes . Les Belles Lettres, Paris 2013, ISBN 978-2-251-00582-9 (critical edition with French translation and commentary)
- Duane W. Roller: Eratosthenes' Geography. Fragments collected and translated, with commentary and additional material. Princeton University Press, Princeton / Oxford 2010, ISBN 978-0691-14267-8 (English translation, commentary, maps).
poetry
- John U. Powell (Ed.): Collectanea Alexandrina . Clarendon Press, Oxford 1925 (contains pp. 58-64 fragments of the seals).
- Alexandra Rosokoki (ed.): The Erigone des Eratosthenes. An annotated edition of the fragments . Winter, Heidelberg 1995, ISBN 3-8253-0299-7 .
History
- Felix Jacoby (ed.): The fragments of the Greek historians . Part 2, Volume B, Weidmann, Berlin 1929 (contains pp. 1010-1021, No. 241 Eratosthenes fragments).
Mathematical and philosophical
- Heinrich Dörrie (Ed.): The Platonism in antiquity , Volume 1: The historical roots of Platonism , Frommann-Holzboog, Stuttgart-Bad Cannstatt 1987, ISBN 3-7728-1153-1 , pp. 116-133 (Greek texts with German translation) and pp. 350–382 (commentary).
Philological
- Andreas Bagordo (ed.): The ancient treatises on drama. With a collection of the fragments . Teubner, Stuttgart 1998, ISBN 3-519-07660-8 , pp. 127–136 (critical edition of the fragments of Über die Alte Komödie ), pp. 37–40 (introduction to the fragments).
literature
- Pedro Pablo Fuentes González: Ératosthène de Cyrène . In: Richard Goulet (ed.): Dictionnaire des philosophes antiques . Volume 3, CNRS Éditions, Paris 2000, ISBN 2-271-05748-5 , pp. 188-236 (extensive research overview).
- Klaus Geus : Eratosthenes of Cyrene. Studies on the Hellenistic cultural and scientific history . Beck, Munich 2002, ISBN 3-406-48976-1 .
- Dieter Lelgemann : Eratosthenes of Cyrene and the measuring technology of the ancient cultures , Chmielorz Verlag, Wiesbaden, 2001, ISBN 978-3-871-24260-1
- Doris Meyer: Eratosthenes . In: Bernhard Zimmermann , Antonios Rengakos (Hrsg.): Handbook of the Greek literature of antiquity. Volume 2: The Literature of the Classical and Hellenistic Period. CH Beck, Munich 2014, ISBN 978-3-406-61818-5 , pp. 100-109
- Alexandra Rosokoki, The Erigone des Eratosthenes. An annotated edition of the fragments , Heidelberg: C. Winter-Verlag 1995
- Rudolf Pfeiffer : History of Classical Philology . 2nd Edition. Beck, Munich 1978, ISBN 3-406-03751-8 , pp. 191-212.
- Eduard Schwartz : Characters from antiquity . 4th edition. Koehler & Amelang, Leipzig 1956, pp. 183-209 (overall assessment).
Web links
- Literature by and about Eratosthenes in the catalog of the German National Library
- DR Dicks: Eratosthenes, Dictionary of Scientific Biography
- Daniela Friedl: How Eratosthenes measured the earth
- Michael Fowler: Measuring the Solar System
- John J. O'Connor, Edmund F. Robertson : Eratosthenes of Cyrene. In: MacTutor History of Mathematics archive . [biographical information partly out of date]
Remarks
- ↑ On the dating Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 10–15; Pedro Pablo Fuentes González: Ératosthène de Cyrène . In: Richard Goulet (ed.): Dictionnaire des philosophes antiques , Vol. 3, Paris 2000, pp. 188–236, here: 190f .; Giorgio Dragoni: Introduzione allo studio della vita e delle opere di Eratostene . In: Physis Vol. 17, 1975, pp. 41-70, here: 46-48.
- ↑ On his Platonism see Friedrich Solmsen : Eratosthenes as Platonist and Poet . In: Solmsen, Kleine Schriften , Vol. 1, Hildesheim 1968, pp. 203-224.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 18f .; Rudolf Pfeiffer: History of Classical Philology , 2nd edition, Munich 1978, p. 192f.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 24f .; Pedro Pablo Fuentes González: Ératosthène de Cyrène . In: Richard Goulet (ed.): Dictionnaire des philosophes antiques , Vol. 3, Paris 2000, pp. 188–236, here: 197.
- ↑ Gottfried Albert Keller: Eratosthenes and the Alexandrian star poetry , Zurich 1946, p. 134f .; Pedro Pablo Fuentes González: Ératosthène de Cyrène . In: Richard Goulet (Ed.): Dictionnaire des philosophes antiques , Vol. 3, Paris 2000, pp. 188–236, here: 190f. (with an overview of the older literature on the question).
- ↑ For the chronological classification see Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 26–30; Pedro Pablo Fuentes González: Ératosthène de Cyrène . In: Richard Goulet (ed.): Dictionnaire des philosophes antiques , Vol. 3, Paris 2000, pp. 188–236, here: 193, 199.
- ↑ Pedro Pablo Fuentes González: Ératosthène de Cyrène . In: Richard Goulet (ed.): Dictionnaire des philosophes antiques , Vol. 3, Paris 2000, pp. 188–236, here: 200; Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 30.
- ↑ Suda , keyword Eratosthenês ( Ἐρατοσθένης ), Adler number: epsilon 2898 , Suda-Online .
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 41f. and on the dating of death p. 15; Pedro Pablo Fuentes González: Ératosthène de Cyrène . In: Richard Goulet (Ed.): Dictionnaire des philosophes antiques , Vol. 3, Paris 2000, pp. 188–236, here: 191f.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 209f.
- ↑ Aristotle, De caelo 2.14 (298a15-17).
- ↑ See also Lucio Russo : The forgotten revolution or the rebirth of ancient thought , Berlin 2005, p. 313.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 235f. Donald Engels disagrees: The Length of Eratosthenes' Stade . In: American Journal of Philology Vol. 106, 1985, pp. 298-311; he thinks that Eratosthenes used the "Attic" stadium of 184.98 m.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 262 and notes 8 and 9; Duane W. Roller: Eratosthenes' Geography , Princeton / Oxford 2010, p. 1.
- ↑ For the shape of the map, see Klaus Zimmermann : Eratosthenes' chlamys-shaped world: a misunderstood metaphor . In: Daniel Ogden (Ed.): The Hellenistic World. New Perspectives , London 2002, pp. 23-40.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 142, 192–194.
- ↑ Heinrich Dörrie (Ed.): The Platonism in the Antike , Vol. 1, Stuttgart-Bad Cannstatt 1987, pp. 351, 355, 361f., 367-386.
- ↑ Hans-Joachim Waschkies : Beginnings of arithmetic in the ancient Orient and among the Greeks , Amsterdam 1989, pp. 280–288; Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 189.
- ↑ Hans Krämer : Eratosthenes . In: Outline of the History of Philosophy . The philosophy of antiquity , Vol. 3: Older Academy - Aristoteles - Peripatos , ed. Hellmut Flashar . 2nd edition, Basel 2004, p. 126. On the teaching of the soul of Eratosthenes see also Friedrich Solmsen: Eratosthenes as Platonist and Poet . In: Solmsen, Kleine Schriften , Vol. 1, Hildesheim 1968, pp. 212-216.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 185f.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 190f.
- ↑ Amin A. Muwafi, Andreas N. Philippou: An Arabic Version of Eratosthenes on Mean Proportionals . In: Journal for the History of Arabic Science Vol. 5, 1981, pp. 147-165. See also Richard Lorch: A Note on the Technical Vocabulary in Eratosthenes' Tract on Mean Proportionals . In: Journal for the History of Arabic Science Vol. 5, 1981, pp. 166-170.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 133–135, 195–205 pleads for the authenticity of the letter, which is usually regarded as a forgery, and offers a German translation on pp. 196–200.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 64–68; Translation of the fragment p. 61f.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 333-335.
- ^ Felix Jacoby (ed.): The fragments of the Greek historians , Part 2, Volume B, Berlin 1929, pp. 1042-1044. See also Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 311f.
- ↑ The Fragments of the Greek Historians No. 241, Fragment 1a; see Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 314–316.
- ↑ See also Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 102-108 with a discussion of the older literature. Geus rejects a connection with the tragedy and considers the mention of the goat in the verse to be a tradition error. Alexandra Rosokoki (ed.): Die Erigone des Eratosthenes , Heidelberg 1995, pp. 84–86, has a different opinion .
- ↑ See Friedrich Solmsen: Eratosthenes as Platonist and Poet . In: Solmsen, Kleine Schriften , Vol. 1, Hildesheim 1968, pp. 211f .; Walter Burkert : Kleine Schriften III: Mystica, Orphica, Pythagorica , Göttingen 2006, p. 257f.
- ↑ On the use of this term as a self-designation see Albrecht Dihle : Eratosthenes und other philologists . In: Manuel Baumbach et al. (Ed.): Mousopolos Stephanos. Festschrift for Herwig Görgemanns , Heidelberg 1998, pp. 86–93; Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 39f .; Rudolf Pfeiffer: History of Classical Philology , 2nd Edition, Munich 1978, pp. 198-200.
- ^ Rudolf Pfeiffer: History of Classical Philology , 2nd edition, Munich 1978, pp. 195f .; Giorgio Dragoni: Introduzione allo studio della vita e delle opere di Eratostene . In: Physis Vol. 17, 1975, pp. 41-70, here: 58-62.
- ↑ On the use of surnames see Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 31–41.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 31f. and note 147; Heinrich Dörrie (ed.) judges differently: Platonism in antiquity , vol. 1, Stuttgart-Bad Cannstatt 1987, p. 353f.
- ↑ On Strabon's criticism of Eratosthenes see Johannes Engels : The Strabonian cultural geography in the tradition of ancient geographic writings and their significance for ancient cartography . In: Orbis Terrarum Vol. 4, 1998, pp. 63-114, here: 73, 76-81.
- ↑ Pedro Pablo Fuentes González: Ératosthène de Cyrène . In: Richard Goulet (ed.): Dictionnaire des philosophes antiques , Vol. 3, Paris 2000, pp. 188–236, here: 194.
- ↑ Johannes Engels: The Strabonian cultural geography in the tradition of ancient geographical writings and their significance for ancient cartography . In: Orbis Terrarum Vol. 4, 1998, pp. 63-114, here: 79f.
- ↑ Details from Georg Knaack : Eratosthenes . In: Paulys Realencyclopadie der classischen Antiquity Science (RE). Volume VI 1, Stuttgart 1907, Sp. 358-389, here: 374.
- ↑ Konrad Gaiser: Das Philosophenmosaik in Neapel , Heidelberg 1980, p. 106 and note 212.
- ^ National Archaeological Museum, Naples , Inv. No. 906; see also Klaus Geus: Eratosthenes von Kyrene , Munich 2002, p. 8 note 6.
- ↑ For the research discussion see Roger Ling, review by Michael Pfrommer : Götliche Fürsten in Boscoreale , Mainz 1993. In: Gnomon 71, 1999, pp. 461–464.
- ^ National Archaeological Museum, Naples, Inv. No. 124545; Konrad Gaiser: Das Philosophenmosaik in Neapel , Heidelberg 1980, pp. 97-103.
- ↑ Pedro Pablo Fuentes González: Ératosthène de Cyrène . In: Richard Goulet (ed.): Dictionnaire des philosophes antiques , Vol. 3, Paris 2000, pp. 188–236, here: 235.
- ↑ Klaus Geus: Eratosthenes von Kyrene , Munich 2002, pp. 337–342; Rudolf Pfeiffer: History of Classical Philology , 2nd Edition, Munich 1978, pp. 191, 195f., 203f., 206–208; Ernst Paul Wolfer: Eratosthenes of Cyrene as mathematician and philosopher , Zurich 1954, pp. 1f., 61, 64.
| personal data | |
|---|---|
| SURNAME | Eratosthenes |
| ALTERNATIVE NAMES | Eratosthenes of Cyrene |
| BRIEF DESCRIPTION | Greek mathematician, geographer, astronomer, historian, philologist, poet, head of the Alexandria library |
| DATE OF BIRTH | between 276 BC BC and 273 BC Chr. |
| PLACE OF BIRTH | Cyrene |
| DATE OF DEATH | around 194 BC Chr. |
| Place of death | Alexandria |