lunar eclipse
During a lunar eclipse ( Austro lunar eclipse ) passes through the moon the shadows , to that of the sun -lit Earth casts in space. This astronomical event can only occur if the sun, earth and moon are sufficiently precisely on one line. Seen from the earth, the sun and moon stand opposite each other. It is a full moon , and from Earth the lunar eclipse can be seen wherever the moon is currently above the horizon or where it is night.
This event can be clearly perceived when the moon not only runs through the ring-shaped penumbra of the earth, but also wholly or partially through the circular inner umbra . Colloquially, a lunar eclipse is usually an umbra eclipse . Penumbral eclipses are hardly noticeable and are only counted in astronomy . In both cases, a distinction is made between total and partial eclipses, depending on whether the moon is completely or only partially immersed in the respective shadow.
The lunar orbit plane is inclined to the ecliptic (orbit plane of the earth around the sun). There are only two moments per orbit when the moon is in the same plane with the sun and earth. Within a few hours before or after a full moon, this only occurs with every sixth, sometimes even a fifth full moon. An average of 154 umbra eclipses occur per century. Penumbral eclipses occur about 88 times per century.
Basics
Formation of lunar eclipses

A lunar eclipse can occur at moon positions 1 and 4 , a solar eclipse at 2 and 3 .
(not to scale, inclination of the lunar orbit increased)
When the moon is full , the moon is in opposition to the sun. It is usually not in the plane of the earth's orbit around the sun ( ecliptic ), since the plane of the moon's orbit is inclined by a good 5 ° to the ecliptic. A lunar eclipse occurs only when the moon is sufficiently close to one of the two imaginary intersections of the ecliptic plane and the lunar orbit , called the lunar node , at the full moon .
From a lunar eclipse to the following full moon, around one synodic month passes as the mean duration of a lunation . In some cases a lunar eclipse can occur again, but in most cases not because the distance to the lunar node is too great. The moon then no longer passes through the knot at full moon, and the so-called knot line - the imaginary connection between the two lunar knots - is therefore no longer directed towards the sun. Thus there is no eclipse during this orbit of the moon. At the sixth full moon in a row, however, the moon is again very close to one of the nodes, this time the other, and thus an eclipse is possible. It takes place when the distance to the node is again so small that a certain node distance, called the darkness limit , is not reached.
After the six lunations , which last a little less than half a year with about 177 days, the earth has not yet completed half of its orbit (or 180 °). After this time, the opposite knot is also not exactly opposite the starting position, because the knot line has turned slightly in the opposite direction and already points back to the sun after about 173 days (half an eclipse year ).

In relation to the nodal passage, the full moon is therefore delayed by about four days after six moon phase cycles, and the nodal distance has changed by an amount of about 4 ° (measured on the ecliptic). When the distance measured to the node has become greater than 4.7 ° , the moon is no longer completely within the umbra, but a partial umbra eclipse can occur. The moon no longer runs through the umbra at a knot distance of around 10.6 ° and only penumbral eclipses are possible; beyond around 16.7 ° it is also outside the penumbra.
With an inconspicuous eclipse through the penumbra, such a cycle of almost half-yearly eclipses one after the other ends and a semester cycle - with the eclipse period of about 177 days the basic cycle of all eclipse cycles - is ended. Sometimes, however, towards the end of a semester cycle - as shown in the figure - the full moon earlier by one lunation is within the (western) eclipse limit. With this darkness a new semester cycle has already started. Its next eclipse takes place five lunations after the last eclipse of the previous cycle.
During the first eclipses of a cycle, the full moon gradually approaches the node, reaches the smallest distance (as the most conspicuous event) and moves away again until the eastern eclipse limit is exceeded and the cycle is over. A semester cycle contains 8 to 10 lunar eclipses and lasts around four years, whereby it can overlap with other semester cycles. More than half of the events are conspicuous, and inconspicuous penumbral eclipses take place at the beginning and end of a cycle.
visibility
In contrast to a solar eclipse , a lunar eclipse can be seen from any place on the night side of the earth and - apart from the position relative to the horizon - offers the same view everywhere. Seen locally, in relation to a fixed location, a lunar eclipse can therefore be observed far more frequently than a solar eclipse. Viewed globally, related to the globe as a whole, solar eclipses occur more frequently than the noticeable lunar eclipses in the umbra of the earth.
Even for a total lunar eclipse, the exact time of entry and exit into or out of the umbra cannot be precisely predicted with an earthly perspective. Not only is the umbra edge blurred and not easy to distinguish from the adjacent penumbra, a remaining fine edge strip in the penumbra would not be visible to the naked eye from the earth.
Difficulties in forecasting
The prediction of eclipse dates is one of the more difficult astronomical tasks, since when determining the orbit of the celestial bodies earth and moon, numerous influences have to be taken into account, which fluctuate periodically or change over long periods of time and have the effect of orbital disturbances . Because of the interaction of body an exact solution for this is multi-body problem is not possible, but only an approximation by numerical methods of modeling. The extent to which these approximations apply can be confirmed or improved on the basis of observation data.
The shadow cast by the earth also does not exactly match the geometric model, since the sun has a certain variable brightness outside of its photosphere, which appears as a “solar disk” (see solar corona and protuberance ). The refraction of sunlight in the earth's atmosphere is also neglected in the calculation.
Types of lunar eclipses
According to the depth of the immersion in the earth's shadow in the phase of the greatest darkening of the moon, umbra and penumbral eclipses are distinguished, and total from partial eclipses.
Total umbra eclipse
If the moon completely ("totally") enters the umbra of the earth during the eclipse , it is a total umbra eclipse , also called a total lunar eclipse . The sunlight falling through the layers of air in the earth's atmosphere is refracted inward, whereby the short-wave blue components in particular are weakened by scattering. Therefore, the moon is still reached by the long-wave red components in the umbra of the earth and remains faintly visible. The sight of the moon, which is darkened brown-reddish during a umbra eclipse , is colloquially also called copper moon or blood moon . The maximum possible duration of a total lunar eclipse is about 106 minutes.
Central (umbra) darkness
If the moon touches not only the umbra but also the central line of the umbra, one speaks of a central eclipse . This is always a total umbra eclipse, as the diameter of the moon is always significantly smaller than the radius of the umbra.
Partial umbra eclipse
If the moon only partially (“partially”) enters the umbra of the earth during the eclipse , it is a partial umbra eclipse . Parts of the moon therefore remain outside the umbra during the entire duration of the eclipse; they are either in the penumbra or are not eclipsed at all in the narrow penumbra (moon near the earth).
The edge of the umbra cast by the earth is shown on the surface of the moon. As at the beginning and end of a total umbra eclipse, the umbra border becomes visible as a curved line. Even the ancient Greeks interpreted this as the shadow cast by the earth and concluded from their circular shadow that the earth was a sphere .
Total penumbral eclipse
If the moon completely enters the penumbra during the eclipse without touching the umbra, it is a total penumbra eclipse . The part of the moon facing the umbra is noticeably darker than the part facing away. Total penumbral eclipses are rare, as the ring of penumbra, even in the best case scenario, is only a maximum of 11 percent wider than the diameter of the moon and the moon has to pass through the penumbra almost perfectly. The last total penumbral eclipse took place on March 14, 2006, the next will take place on August 29, 2053.
If the penumbra is narrower than the diameter of the moon, no total penumbral eclipse can occur, only partial penumbra or partial umbra eclipses are possible. In very rare cases (as on April 25, 2013) it can happen that even in the phase of maximum eclipse the moon is partially in the umbra, in the penumbra and outside the shadow at the same time.
Partial penumbral eclipse
If the moon only partially enters the penumbra during the eclipse, it is a partial penumbra eclipse . The moon is hardly noticeably darkened. Only from a penumbral magnitude of 0.7 is an eclipse of the side facing the umbra clearly visible with the naked eye. Partial penumbral eclipses of the moon are relatively common. Since its diameter is almost as large as the width of the ring of the penumbra, it occurs about as often as partial umbra eclipses.
frequency
Averaged over several centuries, penumbral eclipses are roughly half as frequent as umbra eclipses (37 percent and 63 percent; around 88 and 154 events per century). Umbra eclipses occur somewhat less often as total than as partial eclipses (29 percent and 34 percent of all lunar eclipses; about 70 or 84 events per century).
In the 21st century, however, significantly more total (85) than partial (57) umbra eclipses are to be expected, because the moon passes through its wider shadows more frequently in this century than on average during a full moon near the earth.
Parameters
Magnitude (or size)
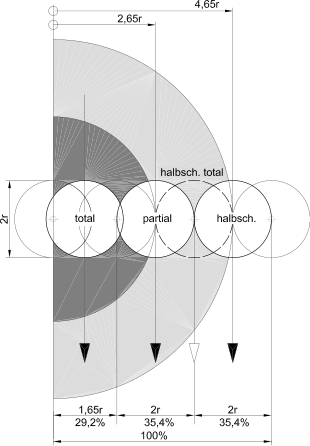
The magnitude or size of a lunar eclipse is a measure of the depth of the moon's penetration into the earth's shadow. The distance between the edge of the moon closer to the center of the shadow and the edge of the shadow closer to the moon is measured on a straight line drawn through the middle of the shadow and the middle of the moon. The measured value related to the diameter of the moon represents the magnitude of the eclipse.
For umbra eclipses, the penetration into the umbra ( lat. Umbra ) is measured. On average, the umbra diameter is about 2.63 times the diameter of the moon; at this ratio the umbral magnitude can vary between 0 and 1.815. Values between 0 and 1 indicate a partial, values from 1 a total eclipse form.
For penumbra eclipses, the penetration into the penumbra (lat. Penumbra ) is measured. The ratio of penumbra width and moon diameter is on average around 1.03 . In the case of a partial penumbral eclipse, the penumbral magnitude is between 0 and 1. Values from 1 indicate a total penumbral eclipse ; it can only occur when the penumbra is at least as wide as the moon.
Danjon scale
Total umbra eclipses can also be characterized by the brightness and color of the umbra as a result of the light refracted by the earth's atmosphere. Depending on the degree of pollution of the atmosphere (especially the stratosphere ), there are differences, for example dark or very dark eclipses can occur after explosive volcanic eruptions with strong ash emissions . André Danjon proposed the following simple scale to characterize the observed brightness (as parameter L ), the Danjon scale named after him :
- L = 0: very dark darkness; Moon almost invisible, especially in the middle of totality
- L = 1: dark darkness; gray or brownish coloration; Details of the lunar surface are difficult to see
- L = 2: deep red or rust-red darkness, with a very dark center, but a relatively light edge of the umbra
- L = 3: brick-red darkness, usually with a light or yellowish edge of the umbra
- L = 4: very light copper-red or orange eclipse with a very light bluish umbra edge.
calculation
Distance of the moon from the center of the earth's shadow
An essential parameter for describing a lunar eclipse is the distance of the moon from the center of the earth's shadow, usually specified as the angular distance ( viewing angle ). The vertex of the viewing angle is the center of the earth. The reference axis is the straight line leading from the sun through the center of the earth to the center of the earth's shadow. It is the polar axis of the spherical coordinate system used as a reference system to represent the viewing angle .
The output variables of the calculation are the equatorial angular coordinates ( ephemeris ) of the sun and moon, their right ascension and declination .
The positive side of the polar axis points towards the moon (away from the sun, towards the opposing sun ). Thus, the equatorial angular coordinates and the polar axis result from the ephemeris of the sun as follows:
During the transformation between angle coordinates, the respective Cartesian coordinates are converted into one another in an intermediate step. Since only the summarizing viewing angle can be determined, the resultant can already be formed from the x and y coordinates of the moon in the reference system (z axis = polar axis) and the viewing angle can be calculated from this immediately. In this case, the directions of the x and y axes are arbitrary. In the following, the y-axis has remained in the equatorial plane. It points to the east, and the x-axis complements a right system :
These Cartesian coordinates are normalized to the distance between the earth and the moon.
The desired viewing angle for the distance of the moon from the center of the earth's shadow is:
- Calculation of x and y
For the calculation, the equatorial coordinates of the unit vector for the moon position and the rotation matrix for the coordinate rotation from the equatorial to the reference system are required and multiplied with each other:
Multiplication:
Radii of the earth's shadow and viewing angles for contacts
The radii and umbra and penumbra can also be specified as viewing angles. They are considered to be constants, since the distances between the sun, earth and moon hardly change during an eclipse. Together with the moon radius (also given as the angle of vision), the distances ( in the sketch opposite) of the moon from the center of the earth's shadow can be calculated, which characterize the contacts of the moon with the shadow edges:
- Entry and exit of the moon in from the penumbra
- Entry and exit of the moon in from the umbra
- Beginning and end of total darkness
From a calculated at short time intervals series of positions of the moon in Earth's shadow, the at the predetermined viewing angles can be associated with contact times interpolate.
- Calculation of and
As parallaxes and specified distances of the sun and moon from the earth are angles of view. The radius of the sun is also given as the viewing angle .
From the triangle EM'V 2 follows
- ,
and from the triangle ES'V 2 follows
- .
Then:
- .
is to be determined with the help of an analog sketch (the edge lines of the penumbra touching the sun and earth intersect between the sun and earth at point V 1 ) and with analog calculations.
Due to the effect of the earth's atmosphere, the actual radii of the core and penumbra are enlarged compared to a purely geometric calculation, which must be taken into account when calculating the contact times by making appropriate corrections in the astronomical elements .
Astronomical elements
The sizes , , , , , , and are astronomical elements are the occasional "Bessel elements of a lunar eclipse" called. However, there is only a mathematical, formal and not a factual relationship to the Bessel elements formulated primarily in the treatment of solar eclipses in an intermediate step . This only applies to two of the eight astronomical elements in both cases: The expressions for the elements x and y only have the same basic form as the result of a coordinate transformation , and the associated coordinate system is not identical to the other.
Optical effects during a lunar eclipse
Reddish color
The moon, which lies completely in the umbra of the earth in a total eclipse, is still faintly recognizable as a reddish blood moon. The reason for this is that the sunlight that reaches the moon has traveled several hundred kilometers through the earth's atmosphere . Due to Rayleigh scattering on the molecules of the earth's atmosphere, the short-wave blue parts of the white sunlight are scattered much more strongly in other directions than the long-wave red parts. As a result, the light passing through the earth's atmosphere consists almost entirely of reddish components. The atmosphere deflects the sunlight by a maximum of 2.2 ° inwards (see also terrestrial refraction ). Therefore, it partially penetrates the umbra of the earth and thus also hits the surface of the moon.
The following images show the same image of a lunar eclipse as it emerges from the umbra in the three primary colors red, green and blue. In the area on the left struck by direct white sunlight, all three primary colors have a high intensity. To the right, towards the umbra center, the intensity decreases for all three colors. The right half of the moon is hardly reached by blue light, and the green light is extremely weak in the right quarter of the moon. In the umbra there are almost exclusively the red light components that are responsible for the naming of a blood moon.
- Lunar eclipse in the three primary colors red, green and blue
brightness
In a central eclipse takes apparent visual brightness of the moon from about -12 m , 5 to about +2 m by a factor of 600,000 from. In the center of the umbra, the decrease in intensity (the decrease in brightness that an observer would notice on the lunar surface) is even 1 to 2 million, around a hundred times more than in a total solar eclipse .
The lunar eclipses in recent years were mostly bright, around L = 3, which suggests a relatively clean stratosphere. After the eruption of the Pinatubo volcano in 1991, some very dark eclipses were observed. In such an eclipse, the moon's brightness can drop to about +5 m , corresponding to a factor of 10 million. The intensity in the center also decreases by about the same factor; the lower limit is determined by the light of the corona of the sun , which is only partially covered by the earth. Thus, the color and brightness of the eclipsed moon allow conclusions to be drawn about the purity of the earth's atmosphere. Today, however, this method is out of date, as measurements from satellites or aircraft provide much more precise information about air pollution than pure optical shadowing allows.
Enlargement of the earth's shadow
Another interesting effect is the enlargement of the earth's shadow. Anyone who has already telescoped a lunar eclipse will have noticed that the contact times often deviate from the calculated values. In fact, because of the atmosphere, the Earth's shadow cone appears about 2 percent larger, an effect already pointed out by Philippe de La Hire in the early 18th century. The umbra edge does not appear sharp, but diffusely washed out.
Photographic recording
A photograph of the moon in the umbra is because of the low luminance a relatively demanding task. Depending on the reception conditions is exposure value well below 1 EV.
The greater the angle of elevation of the moon when the picture is taken, the less atmospheric disturbances are , which lead to the blurring of contours in the images. In the same way, the attenuation of light due to the extinction in the earth's atmosphere also decreases with increasing distance from the horizon.
Distance adjustment
In practice, the lens can be "infinitely" usually on because of the huge distance set are. Since the moon is very far away, the lens must be set to at least the hyperfocal distance for recordings that should not be perceived as a blurred image by humans . In this case, all objects between half the hyperfocal and infinite distance are imaged with sufficient focus. In the case of images that are technically evaluated or from which excerpts are to be used, the distance may have to be set even more precisely according to the requirements.
Exposure time
If the camera is moved with the earth's surface, the image location of the moon shifts over time, so that there is a motion blur in the image. This can be compensated by rotating the camera around the earth's axis with a suitable device . Alternatively, movable image sensors can also be used for this purpose (see for example "Astro Tracer" of the Pentax K-1 ).
Otherwise the maximum exposure time must be limited so that the motion blur cannot be seen. With a given angle of view in degrees, the following rule of thumb can be used to estimate the maximum exposure time in seconds:
With a fixed, omnidirectional camera (angle of view = 360 °), recordings with an exposure time of one minute are possible if no enlarged image sections are to be used. Format-filling (square) pictures of the moon with a diagonal angle of view of 0.7 ° can only be taken with an exposure time of a good tenth of a second if the camera is not moved during the recording.
For digital still and moving image recordings with longer exposure times, it should be noted that the image sensor heats up during operation and the image noise increases significantly with increasing temperature. Furthermore, with many image sensors, such as active pixel sensors , the image noise increases with the exposure time. For image generation with a high signal-to-noise ratio , the image sensor can be cooled passively or actively . Otherwise, several images can be taken with a limited exposure time and later put together using the software (“stacking”, see below). Exposure times that are too short, however, generate increased readout noise due to the large number of individual images, so a compromise has to be found.
F-number
Since very little light is available, it is advisable to choose the smallest possible f-stops and thus large apertures so that as much light as possible can be captured for the exposure.
Since the image quality of optical systems with a large aperture is limited by image errors , it is recommended to use optically corrected objectives or telescopes, such as aspheres to reduce spherical aberration or apochromats to reduce chromatic aberration . The lateral color error can be automatically compensated for with modern digital camera systems .
Color temperature
For color photos , the color temperature can be set to approx. 4100 Kelvin according to the white-neutral value of the light reflected by the full moon . Higher values, such as the value for direct sunlight of 5500 Kelvin, result in images with a stronger red component, which often comes closer to the subjective association with the color of blood .
Stacking
In order to increase the light yield, image sensors can be used to record series images , which are then superimposed and put together using the software (English: “stacking”). This has the advantage that each individual image is sufficiently free from motion blur and signal interference that increases with the exposure time, but still significantly more light is available for the composite recording. This results in a significantly better signal-to-noise ratio and thus less image noise and a larger dynamic range .
Lunar eclipses
Total lunar eclipses between 1900 and 2100 lasting 100 minutes or more
| date | Duration | date | Duration | date | Duration | ||
|---|---|---|---|---|---|---|---|
| Aug 4, 1906 | 1h 41m | Jul 6, 1982 | 1h 46m | 26 Jun 2029 | 1h 42m | ||
| Jul 16, 1935 | 1h 40m | Jul 16, 2000 | 1h 46m | 7 Jul 2047 | 1h 40m | ||
| Jul 26, 1953 | 1h 41m | Jun 15, 2011 | 1h 40m | 17 Jun 2076 | 1h 41m | ||
| Jun 25, 1964 | 1h 41m | Jul 27, 2018 | 1h 43m | Jun 28, 2094 | 1h 41m |
The date indicates the day on which the middle of the eclipse falls in universal time.
All lunar eclipses from 2014 to 2020
| date | Art | size | entry | Beginning of totality |
maxi mum |
End totality |
exit | Visibility 10 ° east longitude |
please refer | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p | u | Half | core | core | Half | |||||||
| Apr 15, 2014 | Core, totally | 2,318 | 1.291 | 04:53 | 05:58 | 07:06 | 07:47 | 08:24 | 09:33 | 10:37 | not visible | |
| Oct 8, 2014 | Core, totally | 2.146 | 1.166 | 08:15 | 09:14 | 10:25 | 10:55 | 11:24 | 12:34 | 13:33 | not visible | |
| Apr 4, 2015 | Core, totally | 2.079 | 1.001 | 09:01 | 10:15 | 11:57 | 12:01 pm | 12:02 | 13:44 | 14:58 | not visible | |
| 28 Sep 2015 | Core, totally | 2.230 | 1.276 | 00:11 | 01:07 | 02:11 | 02:47 | 03:23 | 04:27 | 05:22 | completely | |
| March 23, 2016 | Half, part. | 0.775 | −0.312 | 09:39 | 11:48 | 13:54 | not visible | |||||
| 16 Sep 2016 | Half, part. | 0.908 | −0.064 | 16:54 | 18:55 | 20:53 | at moonrise | |||||
| Feb 11, 2017 | Half, part. | 0.988 | −0.035 | 22:34 | 00:45 | 02:53 | Completely | |||||
| 7 Aug 2017 | Core, part. | 1.288 | 0.246 | 15:50 | 17:23 | 18:21 | 19:18 | 20:51 | at moonrise | |||
| Jan. 31, 2018 | Core, totally | 2,294 | 1,316 | 10:51 | 11:48 | 12:52 | 13:31 | 14:08 | 15:11 | 16:08 | not visible | |
| Jul 27, 2018 | Core, totally | 2,679 | 1.609 | 17:15 | 18:24 | 7:30 p.m. | 20:23 | 21:13 | 22:19 | 23:29 | at moonrise | |
| Jan. 21, 2019 | Core, totally | 2.168 | 1.195 | 02:36 | 03:34 | 04:41 | 05:13 | 05:43 | 06:51 | 07:48 | Completely | |
| 16 Jul 2019 | Core, part. | 1.704 | 0.653 | 18:44 | 20:02 | 21:32 | 23:00 | 00:18 | Completely | |||
| Jan 10, 2020 | Half, part. | 0.896 | −0.116 | 17:07 | 19:11 | 21:12 | at moonrise | |||||
| Jun 5, 2020 | Half, part. | 0.908 | −0.405 | 16:54 | 18:55 | 20:54 | at moonrise | |||||
| Jul 5, 2020 | Half, part. | 0.355 | −0.644 | 03:07 | 04:31 | 05:52 | Completely | |||||
| Nov 30, 2020 | Half, part. | 0.828 | −0.262 | 07:32 | 09:44 | 11:53 | not visible | |||||
- part .: partial, total: total, core: umbra, half: penumbra
- Times in UTC ( Central European Time : CET = UTC + 1h; Central European Summer Time : CEST = UTC + 2h)
All lunar eclipses of the last and the current century
See also
literature
- Jean Meeus , Hermann Mucke : Canon of the lunar eclipses −2002 to +2526. 3. Edition. Astronomical Office , Vienna 1992
- Fred Espenak : Thousand Year Canon of Lunar Eclipses 1501 to 2500. Astropixels Publishing, Portal 2014, ISBN 978-1-941983-03-4 ( online )
Web links
- Mondfinsternis.info - German-language information, very detailed on each eclipse
- "Ask the stargazer - When will there be a lunar eclipse?" - Video with explanatory animation
- freely scalable sketch of the sun, earth and moon as well as umbra and penumbra of the earth
- NASA - Lunar Eclipse Page (English)
- Robert Harry van Gent: A Catalog of Eclipse Cycles. In: Webpages on the History of Astronomy. September 8, 2003, accessed October 4, 2008 (English, compilation of all cycles in the series of eclipses).
- Lunar eclipse at Bayerischer Rundfunk Wissen - detailed information about the next lunar eclipse in Germany with graphics, photos and explanatory video
Individual evidence
- ↑ entry lunar eclipse in Duden (online).
- ^ J. Meeus: More Mathematical Astronomy Morsels , Willmann-Bell Inc., 2002, Chapter 24 ISBN 0-943396-74-3
- ↑ a b c d J. Meeus, H. Mucke: Canon of the Lunar Eclipses -2002 to +2526 , 3rd edition, p. XXVI. Astronomisches Büro , Vienna, 3rd edition 1992.
- ↑ The fact that the vertex of the viewing angle is different when observing from the surface of the earth means a negligible difference.
- ↑ a b c d P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac, 2nd ed. 1992, pages 467-470 and 428-430
- ^ Siegfried Wetzel: Lunar eclipse and Bessel elements? on-line
- ↑ The Cartesian coordinates X, Y and Z of the lunar unit vector are also preserved.
-
↑ The first rotation takes place around the old Z-axis .
The second rotation takes place around the new y-axis .
The rotation about the new z-axis is omitted: .
- ↑ Jerome Meyer, Dissertation Uni Bremen, 2004 online , Fig. 6.5, value doubled
- ↑ Atmospheric disturbances , Wikibook "Digital imaging methods", chapter "Image acquisition", accessed on July 31, 2018
- ↑ Pentax K-1 camera: SLR camera for high demands , test.de from August 3, 2016, accessed on July 31, 2018
- ↑ Maximum exposure time , Wikibook “Digital imaging methods”, chapter “Image acquisition”, accessed on July 31, 2018
- ↑ Sensor-Rauschen , Stemmer Imaging, accessed on August 3, 2018
- ↑ NASA: Total Lunar Eclipse of 2014 Apr 15. (PDF; 52 kB) Retrieved on December 16, 2012 .
- ↑ NASA: Total Lunar Eclipse of 2014 Oct 08. (PDF; 52 kB) Retrieved on December 16, 2012 .
- ↑ NASA: Total Lunar Eclipse of 2015 Apr 04. (PDF; 50 kB) Retrieved on January 5, 2015 .
- ↑ NASA: Total Lunar Eclipse of 2015 Sep 28. (PDF; 52 kB) Retrieved January 5, 2015 .
- ↑ NASA: Penumbral Lunar Eclipse of 2016 Mar 23. (PDF; 43 kB) Accessed January 5, 2015 .
- ↑ NASA: Penumbral Lunar Eclipse of 2016 Sep 16. (PDF; 44 kB) Retrieved January 5, 2015 .
- ↑ NASA: Lunar Eclipse of 2017 Feb 11. (PDF) Accessed November 1, 2017 (English).
- ↑ NASA: Lunar Eclipse of 2017 Aug 07. (PDF) Retrieved on November 1, 2017 (English).
- ↑ NASA: Lunar Eclipse of 2018 Jan 31. (PDF) Accessed November 1, 2017 (English).
- ↑ NASA: Lunar Eclipse of 2018 Jul 27. (PDF) Retrieved on November 1, 2017 (English).
- ↑ NASA: Lunar Eclipse of 2019 Jan 21. (PDF) Retrieved on November 1, 2017 (English).
- ↑ NASA: Lunar Eclipse of 2019 Jul 16. (PDF) Retrieved on November 1, 2017 (English).
- ↑ NASA: Penumbral Lunar Eclipse of 2020 Jan 20. (PDF) Retrieved on November 1, 2017 (English).
- ↑ NASA: Penumbral Lunar Eclipse of 2020 Jun 05. (PDF) Retrieved on November 1, 2017 (English).
- ↑ NASA: Penumbral Lunar Eclipse of 2020 Jul 05. (PDF) Retrieved on November 1, 2017 (English).
- ↑ NASA: Penumbral Lunar Eclipse of 2020 Nov 30. (PDF) Retrieved on November 1, 2017 (English).
- ↑ NASA Eclipse Web Site
- ^ NASA : Lunar Eclipses: 2011-2020. Retrieved December 10, 2011 .
- ↑ NASA: Lunar Eclipses: 2001-2010. Retrieved December 10, 2011 .