Lunar orbit

The approximately elliptical orbit of the moon around the earth is called the lunar orbit .

Lunar orbit
Mean elliptical geocentric orbital elements , related to the mean ecliptic and the mean equinox for epoch J2000.0
Major semi-axis	383 397.791 6 km
eccentricity	0.055 545 526
Small semi-axis	382 805.89 km
Track length	2,407 100.2 km
Tilt towards the ecliptic	5.156 689 83 °
Length of the ascending node	125.044 555 04 °
Movement of the ascending node	−19.341 361 8 ° / year ( retrograde)
Length of perigee	83.353 242 99 °
Movement of the perigee	+40.690 137 ° / year ( prograd )
Medium length	218.316 654 36 °
Medium sidereal movement	13,176 358 230 557 8 ° / day
The above numerical values ​​are only mean values ​​and only apply to time J2000.0; the orbital elements are sometimes subject to considerable periodic and secular changes.
Inclination of the lunar equator towards the ecliptic	1.542 67 °
Gravitational secular acceleration	+6.0463 ″ / century 2
Tidal secular acceleration	−25.858 ″ / century 2

Since the moon is exposed not only to the gravitational pull of the earth, but also to that of the sun and the other planets , its orbit deviates noticeably from a pure Keplerellipse . The exact orbit calculation is a complicated task, the solution of which is the subject of the lunar theory . Dealing with this problem of celestial mechanics gave the impetus to many important physical and mathematical developments.

Path geometry

Orbit of the moon around the earth, approximated as an ellipse. The moon (right) is shown in a position close to the earth . The moon and earth both revolve around the earth-moon center of gravity , which is located in one of the two focal points (red points) of the ellipse.

In a geocentric frame of reference , in which the earth is regarded as stationary, the lunar orbit approximately represents a Keplerellipse around the earth. However, due to various orbital disturbances , which are mainly caused by the gravitational pull of the sun, this ellipse changes both its shape and its shape in a complicated manner also their position in space. The orbital speed of the moon therefore follows Kepler's second law only very imprecisely.

In a heliocentric reference system, the earth-moon center of gravity describes a Keplerellipse. The moon moves alternately outside and inside the earth's orbit , whereby its orbit is always curved towards the sun (see section heliocentric lunar orbit ).

shape

The orbit of the moon around the earth is variable and approximately an ellipse, its major semi-axis averages 383,398 km and its numerical eccentricity about 0.055. This would correspond to a perigee distance of 362,102 km and an apogee distance of 404,694 km from Earth. Because of the disturbances mentioned, however, both the major semi-axis and the eccentricity (→ path disturbances ) fluctuate , so that larger and smaller extreme distances are also possible. The expected time-average Earth-Moon distance is approximately 385,000 km, for details, see the section Erdabstand .

The moon moves on this track rechtläufig , in the same direction as the Earth and the other planets of the solar system , so the north pole of the ecliptic of view counterclockwise. For an observer on earth an apparent daily movement of the moon can be seen over the horizon as a result of the earth's rotation ; it rises in the east and sets in the west like the sun and stars. But this apparent movement is slower than that of the fixed stars , it remains about 13 ° daily compared to the starry sky and reaches the previous position again after more than 27 days, the period of a sidereal month .

In its orbit around the earth, the orbital speed of the moon averages 1.023 km / s, it fluctuates between 0.964 km / s and 1.076 km / s.

The specification of 383,400 km for the major semi-axis relates to a reference system with a fixed earth. However, the moon does not run on its orbit around the center of the earth , but around the barycenter , the common center of gravity of the earth-moon system , around which both the moon and the earth revolve. According to Kepler's First Law , the common center of gravity lies in the common focal point of both orbital ellipses. Since the lunar mass is about 1 / 81.3 of the earth's mass , the barycentre lies on the average 385,000 km / 82.3 ≈ 4680 km from the center of the earth - so only about 1700 km deep in the earth's mantle . The center of the earth thus runs once a month at an average distance of 4680 km around the center of Barya; the actual orbit ellipse of the moon around the center of Barya accordingly has a large semi-axis of 383,400 km * 81.3 / 82.3 ≈ 378,700 km. The center of the earth, the barycentre and the center of the moon always lie on a common line and in a common plane, the plane of the lunar orbit. Since this is inclined by 5.2 ° to the ecliptic, the center of the earth always runs slightly above or below the ecliptic plane around the sun defined by the course of the barycentre. The earth's ecliptical latitude - its deviation from the ecliptic plane when viewed from the sun - can be up to 0.7 ″.

location

The nodes of the lunar orbit
(inclination i shown exaggerated)

The plane of the lunar orbit is inclined to the orbit plane of the earth, the ecliptic plane , by about 5.2 ° on average. However, the inclination fluctuates with a period of 173 days (half an eclipse year ) by approximately ± 0.15 ° around this mean value (→ orbit disturbances ).

The line of intersection of the earth's and lunar orbit planes (the nodal line ) does not have a fixed orientation in space, as would be the case in the absence of disturbances, but instead performs a full retrograde rotation of 360 ° along the ecliptic once every 18.61 years due to the disturbance (→ Railway disruptions ). Because of this precession movement , the lunar orbit runs alternately above and below a given ecliptic segment over the years, so that the orbit of the moon coincides with the ecliptic plane averaged over one of these precession cycles. This distinguishes the Earth's moon from most other moons, which either orbit on average in the equatorial plane of their planet or, as trapped moons, have very strong orbital inclinations (see Laplace plane ).

The position of the apsidal line , which describes the alignment of the ellipse within the plane of the orbit, does not remain constant either, as the disturbances cause a rotation of the apsis with a period of 8.85 years (→ orbital disturbances ). During this period, the perigee runs once around the entire orbit.

Distance to earth

Medium distance

The temporal arithmetic mean of the variable distance between the centers of the moon and earth is 385 001 km. This can be done e.g. B. from the series expansion of the distance given by Chapront and Chapront-Touzé :

${\displaystyle {\begin{alignedat}{3}{\frac {d}{\mathrm {km} }}=385000{,}5584&\ -\ &20905{,}3550&\cdot \cos(G_{M})\\&\ -\ &\ 3699{,}1109&\cdot \cos(2D-G_{M})\\&\ -\ &\ 2955{,}9676&\cdot \cos(2D)\\&\ -\ &\ \ 569{,}9251&\cdot \cos(2G_{M})\\&\ \pm \ &\dotsc &\end{alignedat}}}$

If the arithmetic mean is calculated using this expression, the cosine terms are dropped and the rounded mean value remains at 385 001 km. (For the meaning of G _M and D see → Fundamental arguments .)

Traditionally, however, 384 400 km are given. This value comes from a different mathematical formulation. The lunar theory of EW Brown gave the distance not directly in kilometers, but as the horizontal parallax of the moon:

${\displaystyle {\begin{alignedat}{3}\pi =0{,}9507245&\ +\ &0{,}0518128^{\circ }&\cdot \cos(G_{M})\\&\ +\ &0{,}0095303^{\circ }&\cdot \cos(2D-G_{M})\\&\ +\ &0{,}0078422^{\circ }&\cdot \cos(2D)\\&\ +\ &0{,}0008571^{\circ }&\cdot \cos(2D+G_{M})\\&\ \pm \ &\dots &\end{alignedat}}}$

If one forms the arithmetic mean here, too, only the constant term remains, and the mean lunar parallax is 0.950 724 5 °. Calculates the distance to the moon from this

${\displaystyle d^{\prime }={\frac {6378{,}14\ {\text{km}}}{\sin(\pi )}}}$

this gives you 384 399 km, which corresponds to the traditional value when rounded.

The two numerical values ​​are not identical, because the mean is taken once over the distance itself and once over its reciprocal value (in the form of parallax), see harmonic mean . From a mathematical point of view, both averaging are equally legitimate.

Extreme distances

The perigee and apogee distances are subject to strong fluctuations.

If the lunar orbit were an undisturbed ellipse, the moon would always pass through the same perigee and apogee distances. However, since the eccentricity of the orbit is subject to periodic changes, there are different extreme distances, depending on how exactly an apsidal passage of the moon coincides with a particularly large or small eccentricity. The eccentricity assumes a maximum every 206 days when the major semiaxis of the lunar orbit points in the direction of the sun. Then the perigee distance is particularly small and the apogee distance particularly large. If the major semi-axis is at right angles to the direction of the sun, then the eccentricity assumes a minimum and the apsidal distances are less extreme. In addition, these changes in orbit are not always the same size and are also subject to long-term drifts. There is therefore a complicated distribution of perigee and apogee distances, without it being possible to specify a clear maximum or minimum value. The more extreme a distance is, the less often it occurs, but there is practically always the possibility of finding an even more extreme value with a sufficient search. Different authors therefore also name extreme values ​​that are rounded differently.

Frequency distribution of the perigee and apogee distances

The following table provides a simplified overview of the distribution of the occurring distances:

	Perigee distance	Apogee distance
smallest:	356 400 km	404,000 km
middle:	363 296 km	405 504 km
largest:	370 300 km	406 700 km

As can be seen, the perigee distances vary significantly more than the apogee distances.

Individual values ​​can also occur outside the specified rounded limits. As record values ​​in the period from 1500 BC Chr. To 8000 AD can be found:

• greatest apogee distance: 406,719.97 km on January 7, 2266
• smallest perigee distance: 356 352.93 km on November 13, 1054 BC Chr.

A particularly small perigee distance is achieved when the moon passes through the perigee as a full moon , the earth is in aphelion and the moon is at its greatest possible distance from the ecliptic ( inclination , i.e. greatest northern or southern latitude). A particularly large apogee distance is achieved when the moon passes through the apogee as a new moon, the earth is in perihelion and the moon has its greatest ecliptic distance.

Orbit periods

Solar and lunar eclipses are only possible if the moon (red) is near a node passage (A and C).

The moon needs an average of 27.32 days to orbit the earth in relation to the fixed star sky. After this sidereal (i.e. star related) month, it passes the same star again as seen from Earth.

During such a month, the earth in turn moves on its solar orbit. This also changes the direction in which the sun appears when viewed from the earth. If the moon has reached its original position with respect to the fixed stars again after a sidereal month, it must also travel about 29 ° in order to reach the same position to the sun and thus the same moon phase again. He needs an average of two days for this; the synodic month, which corresponds to a complete cycle of all moon phases (a lunation ), has a length of 29.53 days. This is the mean time interval with which a moon phase repeats itself (e.g. from full moon to full moon).

Because of the rotation of the apse (see above), the perigee and apogee move along the orbit, in the same direction as the moon itself, so that after completing a sidereal month it has to travel a bit to arrive at the same apse again. The anomalistic month of 27.55 days is the time between two passes of the moon through the perigee or apogee of its orbit and thus the actual orbit period (anomalistic period) of the elliptical orbit.

Because of the precession of the lunar orbit plane (see above), the orbital nodes migrate along the ecliptic, counter to the movement of the moon, so that it returns to the same node earlier than to the same star. The draconian month as the time interval between two passes of the moon through the same knot therefore has an average length of only 27.2 days. Since lunar and solar eclipses can only take place when the moon is in the vicinity of an orbit, there is always an integral number of draconian months between two eclipses that have the moon at the same node. Between any two eclipses there is always an integer number of half draconian months.

The mean lengths of the different months are:

Draconite Month	:	Return to the same railway node,	27 d	5 h	5 m	35.9 s	or	27,212 221 days
Tropical month	:	Return to the vernal equinox,	27 d	7 h	43 m	4.7 s	or	27,321,582 days
Sidereal month	:	Return to the same star	27 d	7 h	43 m	11.6 s	or	27,321,662 days
Anomalous month	:	Return to the same vestibule,	27 d	13 h	18 m	33.1 s	or	27,554 550 days
Synodic month	:	Return to the same phase of the moon,	29 d	12 h	44 m	2.9 s	or	29,530 589 days

The month lengths mentioned are mean values. Since the movements of both the moon and the earth are irregular on their elliptical orbits, individual months can deviate more or less strongly. For example, the duration of a given synodic month can be up to about 7 hours longer or 6 hours shorter than the mean synodic month. In addition, the mean lengths of the month are subject to slow drift due to long-term changes in the orbit of the earth and the moon. For example, the exact length of the middle synodic month is calculated according to

M _syn = 29.5305888531 ^d + 0.00000021621 T - 3.64 · 10 ⁻¹⁰ T ² ,

where T is the number of Julian centuries that have elapsed since the standard epoch J2000.0 .

In a period of 223 synodic months, 242 draconian months also appear almost exactly as whole numbers. After this period of time, the moon will return to both the same phase and the same node. This also repeats the prerequisites for a solar or lunar eclipse , and 223 synodic months after a given eclipse, an eclipse can therefore be expected again. This period of 18 years and 10 1/3 days (or 11 1/3 days depending on the number of leap years included) is the Saros period known as the eclipse period . Since a Saros period also contains almost exactly 239 anomalous months, the moon also has the same distance from the earth and the same great inequality depending on the anomaly (see below), so that the second eclipse is very similar to the first.

Cassini's laws of lunar rotation

Animation: the moon's libration , a result of its elliptical orbit

The essential connections between the moon's own rotation and its orbital movement were recognized by JD Cassini and published in 1693:

1. The moon rotates evenly around its polar axis; its period of rotation is identical to the mean sidereal period of its orbit around the earth.
2. The inclination of the lunar axis against the ecliptic remains constant.
3. The descending node of the lunar equator on the ecliptic coincides with the ascending node of the lunar orbit on the ecliptic and precesses together with it.

These laws describe several observational facts. An earthly observer always sees the same side of the moon. So it obviously revolves around itself once in the same period of time as it once around the earth; this is Cassini's First Law. But while the self-rotation proceeds almost uniformly, the orbit runs along the elliptical orbit at different speeds; In spite of the bound rotation , the exact same sight does not always result during a moon orbit. From the observer's point of view, the orbiting moon seems to perform periodic lateral rotations of up to almost ± 8 °, the libration in length . So you can see once more from the western edge and once more from the eastern edge of the moon. This librational movement was discovered by Hevelius .

For the first time, Hevelius' map of the moon shows the areas of ligation that are only visible when the libration is in a favorable position.

The discovery goes back to Galileo that the moon also performs a nodding movement, the libration in width : at times more can be seen from the north edge and at times more from the south edge of the moon. However, if the axis of the moon were perpendicular to its plane of orbit, it would have to appear unchanged to the observer who is also in the plane of the orbit; the observation showed that the lunar axis was inclined with respect to its orbit. If the axis were z. B. perpendicular to the ecliptic plane, it would be inclined by a good 5 ° to the orbit and the observer could see a nod by a good ± 5 °; However, about ± 7 ° are observed, which are always reached at the maximum ecliptical latitude of the moon. From this it follows that the lunar axis must also be inclined, namely in the form that the northern hemisphere of the moon is inclined a little further away from the earth when it reaches its maximum northern latitude and inclined a little further towards the earth when it reaches its maximum southern latitude . This configuration is described by Cassini's Third Law. It can also be expressed as follows: the perpendicular on the lunar orbit, the perpendicular on the ecliptic and the axis of rotation of the moon lie together in one plane, with the ecliptic perpendicular between the other two. Since the lunar orbit executes a precession movement (→ rotation of the nodal line ), but the described configuration - as the observation shows - is preserved, the axis of rotation of the moon must also execute a precession movement in the same direction and at the same speed as the lunar orbit plane.

The lunar orbit plane is inclined by 5.2 ° to the ecliptic plane and the equatorial plane of the moon is in turn inclined by 6.7 ° to the lunar orbit plane, but in the opposite direction (Third Cassini's law). The inclinations therefore almost cancel each other out, and the lunar equator is only inclined by 1.5 ° to the ecliptic. As a result, solar radiation on the moon is subject to almost no seasonal fluctuations, and at the lunar poles the sun is always close to the horizon.

The lunar equator is inclined by 6.7 ° to the lunar orbit plane and by 1.5 ° to the ecliptic, but the angle between the lunar orbit plane and the ecliptic varies by ± 0.15 ° (→  fluctuation of the orbital inclination ). According to Cassini's Second Law, the inclination of the moon with respect to the ecliptic remains constant, therefore the inclination of the moon with respect to its own orbit varies by ± 0.15 °.

As theoretical celestial mechanics later showed, the Cassini laws describe a dynamically stable state. The longest axis of the moon, described as a three-axis ellipsoid (on average), is always aligned with the earth. This alignment corresponds to a minimum of the gravitational energy and therefore remains stable. In addition, an ellipsoid can only rotate stably (without wobbling) if it rotates around the axis with the largest or the smallest moment of inertia . In the case of the moon, the longest axis (which has the smallest moment of inertia) is held by the earth, as just described, the rotation of the moon therefore takes place around the shortest ellipsoidal axis. In addition, this axis of rotation cannot be exactly perpendicular to the plane of the lunar orbit, since otherwise the earth would lie in the equatorial plane of the moon and could not exert any torque that causes the precession of the lunar axis described in Cassini's Third Law. The inclination adjusts itself (for energetic reasons) in such a way that the precession of the lunar axis takes place at the same rate of movement as the precession of the lunar orbit.

Due to the considerable orbital disturbances, the earth-moon system does not strictly follow the empirically found Cassini laws, but fluctuates around the ideal configuration. The Cassinian laws are therefore only valid when considered on the average.

Railway disruptions

The orbit of the moon can be roughly described as a Keplerellipse . But while an undisturbed Keplerellipse of two point masses would retain both its shape and its position in space, the lunar orbit is subject to numerous additional gravitational influences and changes its shape and position noticeably. The main sources of interference are

1. the earth flattening (deviation of the earth's body from the spherical shape)
2. the gravitational effect of the sun
3. the gravitational effect of the planets (especially Venus and Jupiter).

Fundamental arguments

For the interpretation and calculation of the disturbances explained below, the "fundamental arguments" to be determined for the respective point in time are required, which describe the mean position of the moon and the sun with respect to various reference points:

L M	=	218.316 ° 654 36 + 13.176 358 230 557 8 ° / d ·  t	:	mean ecliptical longitude of the moon (mean distance from vernal equinox )
				Period: a tropical month of 27.32158 days
G M	=	134.963 411 38 ° + 13.064 992 953 630 ° / d ·  t	:	mean anomaly of the moon (mean distance from perigee)
				Period: an anomalous month of 27.55455 days
G S	=	357.529 ° 109 18 + 0.985 600 281 756 0 ° / d ·  t	:	mean anomaly of the sun (mean distance from perihelion)
				Period: an anomalous year of 365.25964 days
D.	=	297.850 204 20 ° + 12.190 749 117 502 ° / d ·  t	:	mean elongation of the moon (mean angular distance from the sun)
				Period: a synodic month of 29.53059 days
F M	=	93.272 099 13.229 + 32 ° 350 240 310 ° / d ·  t	:	mean latitude argument for the moon (mean distance from the ascending node)
				Period: a draconian month of 27.21222 days

Where t is the number of days that have passed since the standard equinox J2000.0 : t = JD - 2451545.0.

Variation of the semi-major axis

Variations in the semi-major axis.

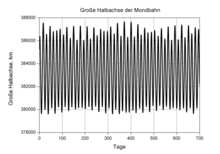
Numerous periodic fluctuations are superimposed on the mean 383 397.8 km of the major semi-axis. The most significant are a variation of ± 3400.4 km with a period of 14.76 days and one of ± 635.6 km with a period of 31.81 days.

As the series development shows

${\displaystyle {\begin{aligned}a=383\;397{,}8\;\mathrm {km} &+3\;400{,}4\;\mathrm {km} \cdot \cos(2D)\\&-\ 635{,}6\;\mathrm {km} \cdot \cos(2D-G_{M})\\&-\ 235{,}6\;\mathrm {km} \cdot \cos(G_{M})\\&\pm \ \dots \end{aligned}}}$

the leading fluctuation term assumes the greatest positive value when the elongation D assumes the value 0 ° or 180 °, i.e. with a new moon and a full moon. The largest negative values ​​of this term arise in the first and last quarter ( D = 90 ° or 270 °).

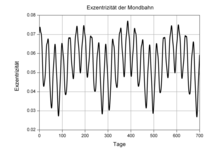
Fluctuation in eccentricity

Fluctuations in eccentricity.

Numerous periodic fluctuations are also superimposed on the mean value 0.055 546 of the eccentricity. The most significant are a variation of ± 0.014 217 with a period of 31.81 days and a variation of ± 0.008 551 with a period of 205.9 days.

The series development

${\displaystyle {\begin{aligned}e=0{,}055546&+0{,}014216\cdot \cos(2D-G_{M})\\&+0{,}008551\cdot \cos(2D-2G_{M})\\&-0{,}001383\cdot \cos(G_{M})\\&\pm \dotsc \end{aligned}}}$

shows that the eccentricity assumes a maximum when the major semiaxis of the lunar orbit points in the direction of the sun (then 2 D - 2 G _M = 0 ° or 360 °, i.e. D = G _M or G _M + 180 °). This happens on average every 205.9 days (a little more than half a year, since the apsidal line moves progressively by 0.11140 degrees per day at the same time). It assumes a minimum when the major semi-axis is perpendicular to the sun (2 D - 2 G _M = ± 180 °).

This fluctuation is superimposed by strong fluctuations over a shorter period (with maxima at 2 D - G _M = 0 ° or 360 °, every 31.8 days) and a large number of smaller fluctuations.

Overall, the eccentricity fluctuates between the extreme values ​​0.026 and 0.077.

Rotation of the knot line

Movement of the ascending node.

The nodal line is not fixed in space, but moves backwards along the ecliptic. The nodes therefore come towards the moon, which is why a draconian month (return to the same node) is shorter than a sidereal month (return to the same fixed star).

The mean speed of this movement in relation to the (even moving) spring equinox is 19.34 ° per year. The nodal line needs 18.6 years for a complete orbit (more precisely 6798.38 days; one orbit with respect to the fixed stars takes 6793.48 days).

Periodic fluctuations are also superimposed on this movement. The largest fluctuation term has an amplitude of 1.4979 ° and a period of 173.31 days. This fluctuation was discovered by Tycho Brahe. It causes the knot line to almost stand still for a short time when it points towards the sun.

Depending on the mutual position of the nodal line of the lunar orbit and the nodal line of the equator, the inclinations of the lunar orbit on the ecliptic and the inclination of the ecliptic on the equator add or subtract, so that the moon with a period of 18.6 years alternately has a declination range of ± 28.6 ° or only ± 18.4 ° covered.

This precession motion of the lunar orbit has the same cause as the precession motion of the earth's axis : the gravitational pull of the sun tries to pull the inclined moon orbit into the ecliptic plane. The moon circling on this orbit reacts like a top that reacts to the external torque by swiveling the lunar orbit axis.

For example, if the moon approaches the descending orbit node, the additional disruptive force acting in the direction of the ecliptic plane causes the moon to approach the ecliptic faster than it would have been without the disruptive force. The moon therefore penetrates the ecliptic earlier and at a steeper angle. The disturbing force pushed the nodal line against the moon and increased the inclination of the orbit. Since the nodal line is shifted in the same direction each time, the result is a constant rotation of the nodes along the ecliptic. The briefly increased inclination of the path, however, is reduced again after passing through the node. The disruptive force now reduces the speed with which the moon moves away from the ecliptic, so that its orbit becomes flatter again. The orbit inclination therefore only experiences a regular fluctuation and does not change constantly in the same sense as the node line.

Fluctuation of the orbit inclination

Fluctuation of the orbit inclination.

The orbit inclination fluctuates about ± 0.15 ° around its mean value. The dominant fluctuation has an amplitude of 0.14 ° and a period of 173.3 days.

The series development

${\displaystyle {\begin{aligned}i=5{,}15668983^{\circ }&+0{,}13507^{\circ }\cdot \cos(2D-2F)\\&\pm \dots \end{aligned}}}$

it can be seen that the inclination assumes a maximum when the nodal line of the lunar orbit points in the direction of the sun (then 2 D - 2 F = 0 ° or 360 °, i.e. D = F or F + 180 °). This happens on average every 173.3 days (a little less than half a year, since the nodal line moves retrograde at the same time by 0.05295 degrees per day). This fluctuation is also superimposed on smaller fluctuations, which occur more pronounced in the minima of the inclination.

The orbit inclination fluctuates because the sun's gravitational pull attempts to decrease the inclination angle by pulling the moon into the ecliptic plane. The effect of the sun is at its maximum when the opening angle between the ecliptic and lunar orbit points in the direction of the sun, i.e. the nodal line is perpendicular to the direction of the sun. It is zero when the nodal line points towards the sun; then the inclination takes on greater values ​​again. The period of 173.3 days is therefore just half an eclipse year and the orbital inclination is always maximum when the sun is close to a node, especially during eclipses.

The fluctuation in the inclination of the orbit was discovered by Tycho Brahe, who - after allusions had already been made - first definitively described it in a letter from 1599.

Rotation of the apse line

Movement of the perigee

Rotation of the apse line

The apse line is also not fixed in the room; it moves in a straight line along the lunar orbit. The apses therefore move in the same direction as the moon, which is why an anomalous month (return to the same apse) is longer than a sidereal month (return to the same fixed star).

The mean speed of the apsid rotation in relation to the vernal equinox is 40.7 degrees per year. The apses need 8.85 years for a complete orbit (more precisely 3231.50 days; one orbit with respect to the fixed stars takes 3232.61 days)

The largest terms of the superimposed fluctuations have an amplitude of 15.448 ° for a period of 31.81 days and 9.462 ° for a period of 205.9 days. In the course of these fluctuations, the pergum can move up to 30 ° from its central position.

The periodic changes in speed and distance of the moon as it traverses its elliptical orbit are caused by the changing tangential and centripetal components of the gravitational force acting on the moon. The disturbances change these force components. In particular, they alternately strengthen and weaken the centripetal forces, but the weakening predominates, as a closer examination shows. The acceleration of the moon in the direction of the earth is thereby reduced, and after one orbit run from the perihelion the moon has not approached the earth again as it would have been without disturbances. The moon takes a little longer to reach perihelion again; the perihelion and thus the entire apsidal line has shifted in the direction of the moon's movement along the orbit.

Disturbances in ecliptical length

If the position of the moon along the ecliptic (its ecliptical length λ) is to be calculated taking into account the perturbation influences, modern perturbation theory provides a comprehensive set of correction terms which - added to the uniformly increasing mean length L _M - results in the correct position. The leading terms of such a calculation are:

${\displaystyle {\begin{alignedat}{3}\lambda =L_{M}&+6{,}289^{\circ }\cdot \sin(G_{M})&\quad &{\text{(Große Ungleichheit)}}&\quad &{\text{( 1)}}\\&-1{,}274^{\circ }\cdot \sin(G_{M}-2D)&&{\text{(Evektion)}}&&{\text{( 2)}}\\&+0{,}658^{\circ }\cdot \sin(2D)&&{\text{(Variation)}}&&{\text{( 3)}}\\&+0{,}214^{\circ }\cdot \sin(2G_{M})&&&&{\text{( 4)}}\\&-0{,}186^{\circ }\cdot \sin(G_{S})&&{\text{(Jährliche Gleichung)}}&&{\text{( 5)}}\\&-0{,}114^{\circ }\cdot \sin(2F_{M})&&{\text{(Reduktion auf die Ekliptik)}}&&{\text{( 6)}}\\&-0{,}059^{\circ }\cdot \sin(2G_{M}-2D)&&&&{\text{( 7)}}\\&-0{,}057^{\circ }\cdot \sin(G_{M}-2D+G_{S})&&&&{\text{( 8)}}\\&+0{,}053^{\circ }\cdot \sin(G_{M}+2D)&&&&{\text{( 9)}}\\&+0{,}046^{\circ }\cdot \sin(2D-G_{S})&&&&{\text{(10)}}\\&+0{,}041^{\circ }\cdot \sin(G_{M}-G_{S})&&&&{\text{(11)}}\\&-0{,}035^{\circ }\cdot \sin(D)&&{\text{(Parallaktische Gleichung)}}&&{\text{(12)}}\\&-0{,}031^{\circ }\cdot \sin(G_{M}+G_{S})&&&&{\text{(13)}}\\&-0{,}015^{\circ }\cdot \sin(2F_{M}-2D)&&&&{\text{(14)}}\\&\pm \dotsc &&&&\\&+{\text{säkulare Akzeleration}}&&&&\\\end{alignedat}}}$

There are similar series developments for the ecliptical latitude and the orbital radius of the moon.

Since the moon attracted the attention of measuring and calculating astronomy very early on, some of the largest terms of disturbance have been known for a long time and even have their own names.

“The discovery and clear distinction of all those perturbations in the lunar orbit that are within the limits of accuracy of a naked eye observation must be counted among the most remarkable achievements of early science. In this way the basis was prepared on which Newton's dynamics could build in order to uncover a unifying explanatory principle for a multitude of apparently incoherent effects. "

- O. Neugebauer : A History of Ancient Mathematical Astronomy

Great inequality

This term is not a disturbance in the actual sense, but merely a consideration of the non-uniform velocity due to the orbital ellipticity. The moon runs faster in the vicinity of the perigee and slower in the vicinity of the apogee than on average. In the case of a mean anomaly G _M of approx. 90 ° or 270 °, it has therefore in each case reached its maximum deviation from the mean position.

In addition to the aforementioned leading term 6.289 ° · sinG _M , the remaining terms of the midpoint equation are also found in the perturbation series

${\displaystyle \nu -G_{M}=\left(2e\cdot \sin(G_{M})+{\frac {5}{4}}e^{2}\cdot \sin(2G_{M})+\dotsc \right){\frac {180}{\pi }}}$

which describes the difference between the true anomaly ν and the mean anomaly G _M for a path of eccentricity e (and thus represents a solution to the Kepler problem). Term 4 of the above perturbation series is the next following term in the midpoint equation. The terms "inequality" or "equation" used in history are to be understood in the sense of "correction".

Overall, the moon can deviate by ± 6.2922 ° from the position of a fictitious steadily moving moon due to the midpoint equation. This significant deviation was already known to ancient astronomers. The Babylonians described it by arithmetic series, the Greek astronomers by a suitably chosen epicyclic .

Evection

→ Main article : Evection

The periodic disturbances of the eccentricity and the position of the perigee deform the orbit in such a way that the moon - following the deformed path - alternately leads or lags the middle position.

If the sun, earth and moon are in a line (S – E – M or S – M – E, full moon or new moon), the sun attracts the earth more strongly than the moon in the first case and the moon more strongly than the earth in the second . In both cases this increases the distance between the earth and the moon and - according to Kepler's third law - reduces the speed of the moon. If the earth and moon are positioned so that their connecting line is perpendicular to the direction of the sun (first or last quarter), both are attracted equally to the sun, but the directions in which they are drawn are not exactly parallel, they converge to the sun down. This results in a component of attraction which brings the moon and earth closer together, whereby the speed of the moon increases - again according to Kepler's third law. The greatest distance to the undisturbed position in the path is always reached when the speed variation just described changes sign and begins to act in the opposite sense. The process just described is also superimposed by a speed fluctuation caused by the eccentricity of the moon's orbit, so that overall a complicated course of the disturbance results.

In the syzygies (2 D = 0 ° or 360 °) the disturbance term is reduced to −1.274 ° sin ( G _M ). The evection is negative if the moon is between perigee and apogee at this point in time (0 <  G _M  <180 °) and positive if the moon is between apogee and perigee (180 ° <  G _M  <360 °). In the quadratures (2 D  = ± 180 °) the opposite conditions prevail.

In the intermediate positions of the moon the course of the evection is more complicated, but it always becomes zero when the sun is in the middle between the moon and the perigee ( D = ½ G _M ), or 90 ° or 180 ° away from this point is. The evection reaches its maximum values ​​of ± 1.274 ° with a period of 31.8 days.

The evection was discovered by Ptolemy after Hipparchus had apparently already noticed signs of deviations from the simple epicyclic model. Ptolemy succeeded in recognizing a pattern in the measured deviations and by introducing a crank mechanism to incorporate it into his epicyclic theory.

variation

→ Main article : Variation (astronomy)

The variation depends only on the elongation D of the moon, i.e. on its angular distance to the sun and thus indirectly on the moon phases. It disappears when the elongation is 0 °, 90 °, 180 ° or 270 °, i.e. with a new moon, a full moon and the two crescent moons. It reaches its maximum values ​​of ± 0.658 ° between these orbital points, i.e. in the so-called octants (45 °, 135 °, 225 °, 315 °). It therefore varies with a period of half a synodic month.

The reason for the variation is that in the octants the angle that the connecting line earth-moon makes to the line of action from the sun to earth and moon is not an integral multiple of 90 ° as in evection, but an 'oblique' component contains, which instead of approaching or moving away causes the moon to slide forwards and backwards with respect to its undisturbed position.

The size of the variation would have allowed ancient astronomers to spot it; however, the Greeks mainly used eclipses for determining the orbit of the moon, where the variation becomes zero and is not noticeable. It was discovered by Tycho Brahe and first mentioned in a letter to Hagecius in 1595 .

Annual equation

The annual equation means that the moon moves a little more slowly when the earth-moon system is in the vicinity of the sun (in the perihelion-side half of the earth's orbit, currently in winter) and a bit faster in the aphelion-side half ( i.e. during the summer). It is subject to a period of one anomalous year and reaches maximum values ​​of ± 0.1864 °.

The annual equation is caused by the eccentricity of the earth's orbit. If the earth-moon system is at a distance from the sun, the gravitational pull of the sun is somewhat less in relation to the gravitational pull of the earth, and the moon is dragged less far away from the earth by the sun. In this situation it is a little closer to the earth and therefore runs faster. In the perihelion, on the other hand, the pull of the sun is stronger, the moon is dragged further away from the earth and moves more slowly. In autumn the moon runs a bit ahead of its middle position, in spring it lags a bit. This is also associated with a fluctuation in the cycle times of ± 10 minutes.

The annual equation was discovered independently by Kepler and Brahe.

Reduction to the ecliptic

The reduction to the ecliptic is again not a disturbance in the strict sense. It serves to take into account the fact that the plane in which the moon moves and along which the orbit coordinate is therefore counted is inclined to the ecliptic plane along which the ecliptical length is counted. The necessary conversion of the orbit coordinate into the ecliptic coordinate can be done by a coordinate transformation or - as here - by a series expansion.

The size of the reduction depends on the mutual distance between the two tilted coordinate planes at the location of the moon and thus on the distance F _{M of} the moon from the ascending orbit node counted along the orbit . The reduction to the ecliptic becomes zero in the orbital nodes and in the middle between the nodes (at F _M = 90 ° and 270 ° ). At F _M = 45 ° , 135 ° , 225 ° and 315 ° it becomes a maximum. So it varies with a period of half a draconian month.

Ptolemy was familiar with this term, but neglected it because of its small size.

Parallactic equation

The parallactic equation assumes maximum values ​​of ± 0.0356 ° and has a period of one synodic month.

It comes about in a similar way to the annual equation. The new moon is closer to the sun than the full moon. It is therefore more strongly dragged away from the earth by the sun and, because of its greater distance, runs slower than the full moon. The therefore slowly accumulating deviation from the undisturbed position is greatest in the crescent phases.

The name of this disturbance comes from the fact that it depends on the ratio of the distance between earth and moon to the distance between earth and sun and therefore allows the distance and thus the parallax of the sun to be determined from a precise examination of the moon's movement. Since the other disturbances depend primarily on the gravitational force of the sun, i. H. on the one hand from their distance, on the other hand also from their mass, cannot be inferred from them without independent determination of the solar mass. The parallactic equation, on the other hand, depends only on the distances and not on the solar mass.

Secular acceleration

In addition to the listed periodic disturbances, the moon is also subject to non-periodic (" secular ") disturbances, which lead to a (positive or negative) acceleration of the moon's course over the millennia.

The "gravitational acceleration" is caused by the fact that the eccentricity of the earth's orbit is currently decreasing. As a result, the sun's gravitational influence on the moon is reduced on average, which - as with the annual and parallactic equations - leads to a slightly faster movement of the moon. This acceleration is 6 ″ / Jhdt ² , so that after t centuries an amount of 6 ″ · t ^{2 has} to be added to the length of the moon.

The " tidal acceleration" works in the opposite direction . The tidal waves piled up by the moon on the earth's oceans are laterally displaced by the earth's rotation, so that they do not lie exactly in the connecting line earth-moon and in turn exert a torque on the moon. This torque supplies angular momentum and energy to the moon, so that it is lifted onto a higher, more energetic orbit, which, according to Kepler's third law, corresponds to a lower orbital speed. This deceleration is about −26 ″ / century ² , so that after t centuries an amount of ½ · 26 · t ^{2 has to be} deducted from the length of the moon. The fact that a factor ½ appears here, in contrast to gravitational acceleration, is only due to corresponding conventions. As a result of the tidal increase in its orbit, the moon moves 3.8 cm away from the earth every year.

Heliocentric lunar orbit

Earth and moon orbits around the sun, section over a month. Around the full moon (at the top of the picture) the curvature of the lunar orbit is greater, towards the new moon (right) less, but still towards the sun. Earth and moon not to scale - the earth would be smaller than the line width.

The moon moves together with the earth at a speed of about 30 km / s around the sun. Its speed fluctuates between just under 29 km / s (in the new moon position) and around 31 km / s (with a full moon). In a sense, it overtakes the earth on the outer orbit when the moon is full, and then falls back behind the earth on the inner orbit when the moon is new. Its path is always curved towards the sun, because its attraction outweighs that of the earth: the sun is almost 400 times further away but has 333,000 times its mass .

Topocentric lunar orbit

In a topocentric reference system, i.e. for the observer on the surface of the rotating earth, the moon, like all other celestial bodies, shows a daily movement . This apparent movement is caused by the rotation of the earth and causes celestial bodies to rise above the eastern horizon and set behind the western horizon. Per hour it is 360 ° / 24 = 15 °, which corresponds to about thirty times the apparent diameter of the moon . However, the actual movement of the moon on its orbit around the earth takes place in the opposite direction. This is easy to determine for an attentive observer: if, for example, the moon is near a certain star at a given point in time, then one hour later it has moved about one moon diameter in an easterly direction with respect to this star. The distance angle is around 13 ° 24 hours later and adds up over the course of a little more than 27 days, a sidereal month, to 360 °, a full turn in front of the fixed star background.

The topocentric lunar orbit deviates from the geocentric lunar orbit due to the parallax : the further away an observer is from the line connecting the centers of the earth and moon, the more the moon deviates from the position it is from this connecting line (or hypothetically from the center of the earth from "seen"). This distance and its direction also change with the rotation of the earth. A stationary observer will therefore observe a corresponding “railway disruption”, the strength of which depends on the geographical latitude of the location.

The following paragraphs therefore describe the diurnal arc of the lunar orbit with geocentric reference to the center of the earth.

With regard to the fixed stars, the moon moves around the sky once in a sidereal month of 27.3 days, i.e. about 13.2 ° on a day on average. The apparent daily rotation of the starry sky in the opposite direction covers this angle in a good 50 minutes. Displaced on average by about this period of time, the highest point of the moon, its culmination , takes place later than the previous one. This delay also applies to the dates of the rising and setting of the moon, if topocentric circumstances such as geographic latitude can be disregarded. The moon rises and sets an average of an hour later than the day before. The new moon rises in the morning together with the sun, in the first quarter the moon rises around noon, then as a full moon in the evening, and in the last quarter only around midnight. The sinking times result with corresponding surcharges. From the knowledge of the moon phase it is possible to estimate the rising and setting times, but only roughly.

The intervals from one culmination to the next can fluctuate by a good quarter of an hour, between 24 ^h  48 ′ and 25 ^h  06 ′. The dates of the rising and setting fluctuate even more. The mean orbital period of the moon in relation to the position to the sun, a synodic month , lasts about 29.5 days, but the lunations from one new moon to the next can differ by more than 3 hours. Over a decade, deviations of more than ± 6 hours from the mean value arise for the duration of a moon phase cycle . Since some of the effects that cause fluctuations in the orbit speed cancel each other out during the entire cycle, the differences in duration become even greater if one considers individual quarters of the phase cycle. The time interval between two phases of the moon - for example in the last quarter of the (waning) crescent to the subsequent new moon - can be more than 20 hours above the average in the 21st century and more than 19 hours less - for example in the second quarter of the (widening) crescent to subsequent full moon (end of June 2003). The average value for a synodic lunar quarter is around 7 days 9 hours.

Since the moon always moves in the vicinity of the ecliptic inclined towards the equator, it sweeps over a similar north-south area as the sun as it traverses its orbit, but not once a year, but once a month. The full moon, the most noticeable phase of the moon, is always opposite the sun in the sky, i.e. it is located in the southern ecliptic section when the sun is in the north (on the northern hemisphere in summer) and vice versa (in winter). Full moons are therefore low in summer and high in the sky in winter. If the moon is in the first quarter, it is high in spring and low in autumn, etc. From the knowledge of the season and the phase of the moon, the height of the culmination and the direction of rise and set can be estimated.

Since the orbit of the moon is inclined by 5 ° to the ecliptic, it covers almost but not exactly the same north-south area as the sun. If the nodal line of its orbit is such that the inclination of the orbit with respect to the ecliptic and the inclination of the ecliptic with respect to the equator add up, then the moon reaches maximum declinations of up to ± 28.6 °; accordingly, its rise and fall points cover a particularly wide area on the horizon (“Big Moon Turn”, most recently in 2006). The winter full moons are then particularly high and the summer full moons particularly low. 9.3 years later, the nodal line has rotated 180 °, the inclinations of the lunar orbit and ecliptic are opposite and the moon only reaches declinations of ± 18.4 °. Its rise and set area on the horizon now has the smallest extent ("Little Moon Turn").

This means that the inclination of the lunar orbit to the earth's equator fluctuates between 18.4 ° and 26.6 °.

Due to the inclination of the lunar orbit towards the ecliptic, the moon can not only cover stars that are on the ecliptic, but also stars that are at a distance of up to ± 6.60 ° on both sides of the ecliptic (to the 5th caused by the orbital inclination) ° the parallax of the moon and its disk radius have to be added). In a given month, however, the moon only covers those stars that are in the immediate vicinity of its current orbit. As a result of the knot precession, the orbit shifts a little with each orbit, and after 18.6 years at the latest the orbit has passed over every accessible star.

In addition, because of this upward and downward movement in relation to the ecliptic, the (upper) culmination (highest level) and meridian passage (level precisely in the south) do not coincide with the moon . For the cumulative effects of the oscillating horizon heights of the culmination in the course of the month, there are the expressions of nosing and obsessing (rising and falling moon).

These calculations of the lunar dates (rise, set, culmination / meridian passage, apparent brightness, and in particular eclipses and coverings) are among the most complex tasks of the ephemeris calculation due to the heavily disturbed orbit of the moon and its proximity to the earth . They belong to the classic sight problems in astronomical phenomenology .

Web links

Wiktionary: Moon orbit  - explanations of meanings, word origins, synonyms, translations

• Java applet: visualization of the path geometry and the disturbances in length (English, Java required)
• H.-D. Gera: moon orbit and Saros cycle.
• Astrolexicon: "The Orbit of the Moon"
• P. Schlyter: Computing planetary positions - a tutorial with worked examples (Instructions for calculating the moon position, English)

Individual evidence

1. ↑ ^{a b c d e f g h} IMCCE: Le manuel des éclipses. EDP ​​Sciences, Les Ulis 2005, ISBN 2-86883-810-3 , p. 32 (Mean orbital elements of the moon for epoch J2000, (online) )
2. ↑ ^{a b c d e f g h i j} J. L. Simon, P. Bretagnon, J. Chapront, M. Chapront-Touze, G. Francou, J. Laskar: Numerical expressions for precession formulas and mean elements for the Moon and the planets . In: Astronomy and Astrophysics . tape 282 , February 1, 1994, p. 663-683 , bibcode : 1994A & A ... 282..663S .
3. ↑ ^{a b} calculated
4. ↑ United States Naval Observatory, Nautical Almanac Office: The Astronomical Almanac for the Year 2009 . United States Government Printing Office , Washington / The Stationery Office, London 2007, ISBN 978-0-11-887342-0 , p. D2.
5. ^ FR Stephenson: Historical Eclipses and Earth's Rotation. Cambridge University Press, Cambridge, UK 1997, ISBN 0-521-46194-4 , p. 11.
6. ↑ ^{a b} J. Chapront, M. Chapront-Touzé, G. Francou: A new determination of lunar orbital parameters, precession constant and tidal acceleration from LLR measurements. In: Astronomy and Astrophysics. vol. 387, 2002, pp. 700-709. (on-line)
7. ↑ ^{a b} NASA: Moon Fact Sheet ( online , accessed June 6, 2011)
8. ↑ ^{a b c d} J. Meeus: Mathematical Astronomy Morsels. Willmann-Bell, Richmond 1997, ISBN 0-943396-51-4 , chapter 4.
9. ↑ The value results from half a year and the rotation of the apse line by about 20 °
10. ^ ^{A b} J. Meeus: Mathematical Astronomy Morsels. Willmann-Bell, Richmond 1997, ISBN 0-943396-51-4 , chapter 2.
11. ↑ ^{a b c d e f g} H.-U. Keller: Astro knowledge . Franckh-Kosmos, Stuttgart 2000, ISBN 3-440-08074-9 , p. 77.
12. ↑ ^{a b c d e} H.-U. Keller (Ed.): Das Himmelsjahr 1992. Kosmos-Verlag, Stuttgart 1991, ISBN 3-440-06238-4 , pp. 82-87.
13. ↑ R. Roncoli: Lunar Constants and Models Document . JPL 2005. ( online ; PDF; 25.5 MB)
14. ↑ PK Seidelmann (Ed.): Explanatory Supplement to the Astronomical Almanac . University Science Books, Mill Valley 1992, ISBN 0-935702-68-7 .
15. ↑ ^{a b c d} D. H. Eckhardt: Theory of the libration of the moon. The Moon and the Planets, vol. 25 (Aug. 1981) pp. 3–49 (online)
16. ↑ H.-U. Keller: Astro knowledge . Franckh-Kosmos, Stuttgart 2000, ISBN 3-440-08074-9 , p. 79.
17. ^ JH Mädler: Popular astronomy. 4th edition. Carl Heymann, Berlin 1852, p. 162.
18. ^ AW Harris, WR Ward: Dynamical constraints on the formation and evolution of planetary bodies . In: Annual review of earth and planetary sciences. vol. 10, 1982, pp. 61-108. (online) , p. 86.
19. ↑ JL Simon, P. Bretagnon, J. Chapront, M. Chapront-Touzé, G. Francou, J. Laskar: Numerical expressions for precession formulas and mean elements for the Moon and the planets. In: Astronomy and Astrophysics. vol. 282, 1994, pp. 663-683. ( online ) p. 669 f. The speeds given there in arc seconds per Julian century have been converted into degrees per day for the sake of clarity (division by 3600 and by 36525). Higher potencies of the time were neglected.
20. ↑ ^{a b c d e} IMCCE: Le manuel des éclipses. EDP ​​Sciences, Les Ulis 2005, ISBN 2-86883-810-3 , p. 34: Fluctuations in the orbital elements of the moon (online)
21. ↑ ^{a b c d e f g h} J. Meeus: Mathematical Astronomy Morsels. Willmann-Bell, Richmond 1997, ISBN 0-943396-51-4 . Chapter 1
22. ^ ^{A b} O. Neugebauer: A History of Ancient Mathematical Astronomy . Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-06995-X , p. 1111.
23. ↑ ^{a b} J. H. Mädler: Popular Astronomy. 4th edition. Carl Heymann, Berlin 1852, p. 159.
24. ↑ TC van Flandern, KF Pulkkinen: Low-Precision Formulas for Planetary Positions. In: The Astrophysical Journal. Supplement Series; 41, November 1979, pp. 391-411. (on-line)
25. ^ O. Neugebauer: A History of Ancient Mathematical Astronomy . Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-06995-X , p. 1108: “The discovery and clear distinction of all lunar perturbations which lie within the limits of accuracy inherent in naked eye observations must be counted among the most remarkable achievements of early science. Thus was prepared the basis upon which Newton's dynamics could build and uncover a unifying principle of explanation for a great variety of apparently disconnected effects. "
26. ↑ JMA Danby: Fundamentals of Celestial Mechanics . Willmann-Bell, Richmond 2003, p. 379.
27. ^ JH Mädler: Popular astronomy. 4th edition. Carl Heymann, Berlin 1852, p. 157.
28. ^ ^{A b} H. Godfray: An Elementary Treatise on the Lunar Theory . Macmillan and Co., London / New York 1885, p. 69 (online)
29. ^ O. Neugebauer: A History of Ancient Mathematical Astronomy . Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-06995-X , p. 84 f.
30. ^ JH Mädler: Popular astronomy. 4th edition. Carl Heymann, Berlin 1852, p. 158.
31. ^ DH Kelley, EF Milone: Exploring Ancient Skies . Springer, New York 2005, p. 34.
32. ^ O. Neugebauer: A History of Ancient Mathematical Astronomy . Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-06995-X , p. 1109.
33. ^ O. Neugebauer: A History of Ancient Mathematical Astronomy . Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-06995-X , p. 1110.
34. ^ O. Neugebauer: A History of Ancient Mathematical Astronomy . Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-06995-X , p. 1107.
35. ^ JH Mädler: Popular astronomy. Carl Heymann, Berlin 1852, p. 160.
36. ↑ ^{a b} F. R. Stephenson: Historical Eclipses and Earth's Rotation. Cambridge University Press, Cambridge, UK 1997, ISBN 0-521-46194-4 , chap. 1.
37. ^ J. Meeus: Mathematical Astronomy Morsels . Willmann-Bell, Richmond 1997, ISBN 0-943396-51-4 , chapter 19.

	This article is available as an audio file:
	Save | Information  | 05:15 min (1.8 MB) Text of the spoken version
	More information on spoken Wikipedia