Earth-moon focus
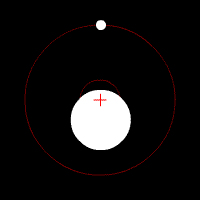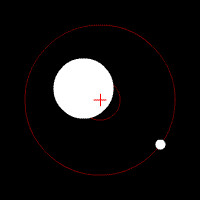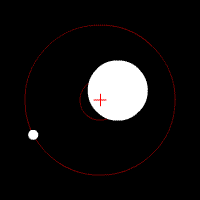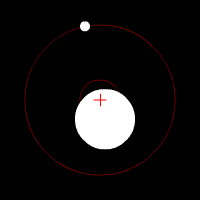
The earth-moon center of gravity is the common center of gravity ( barycenter ) in the earth-moon system . Although the Moon from the Earth seen from ( geocentric ) seemingly around the center of the Earth is rotating , however, both the earth and the moon around their common center of mass and - rotate - in the contemplation of a sun-fixed system. Because of the overwhelming mass of the earth, this is still in the interior of the earth (more precisely: in the earth's mantle ), but does not coincide with the center of the earth .
The lunar orbit is not a circle, but approximately elliptical with the earth-moon center of gravity at a focal point of the ellipse . Due to the eccentricity of the lunar orbit, the earth-moon distance varies by over 13 percent between (on average) 356,410 and 406,740 km in the rhythm of the anomalous month . Both the moon and the center of the earth thus have a varying distance from the earth-moon center of gravity.
The earth-moon system with the earth-moon center of gravity as a common center of gravity orbits the sun as a whole .
Basics
A body rotating in a weightless state always revolves around its center of mass . In relation to external forces, the center of gravity moves as if the entire mass of the body were united in it. For example, the center of gravity of a hammer thrown upwards moves exactly on a parabola, while the hammer rotates around the center of gravity close to the hammer head.
The same applies to a "double body " ( two-body system ) consisting of two celestial bodies, such as B. Earth and moon: their movement in space can be broken down into
- a movement of the common center of gravity on a Keplerian elliptical orbit around the sun, under the influence of the gravitational force exerted by it ; the " earth orbit " around the sun is actually the orbit of the earth-moon center of gravity .
- a rotation of the earth and moon around the common center of gravity. The rotation around each other results in the earth swinging on its orbit around the sun in radial and vertical directions. This effect is called monthly or lunar orbit disturbances (English lunar perturbation ) of the earth or terrestrial disturbances of the moon. Like the phases of the moon, their period is about 29½ days.
calculation
In a first approximation it is sufficient to consider the earth and moon as point masses. The position of the common center of gravity on the line connecting the two centers of mass is determined according to the definition of the center of mass as the distance from the center of the earth and as the distance from the center of the moon :
With
- the point mass of the earth
- the punctiform mass of the moon
- their mean mutual distance
Since the masses of the earth and moon are in a ratio of around 81: 1:
their common center of gravity lies around one eighty-second of the distance between the two centers of mass outside the center of mass of the earth:
so about 4700 km away from the center of the earth in the direction of the moon or about 1700 km below the earth's surface.
Radial fluctuation
While the orbit of the common center of gravity around the sun represents an almost perfect Keplerellipse, the earth leaves this orbit by up to 4700 km. The result is a ripple of approx. 0.03 ‰ (as the quotient of 4700 km and the mean sun-earth distance of one AU ) - a deviation that cannot be seen in true-to-scale representations.
With the moon, however, the fluctuation is still 1.2%. Because the earth is behind the center of the orbit as seen from the moon, the difference between the orbit axis of the lunar orbit and its linear eccentricity is 4700 km or 1.2% smaller than the perigee distance and the sum of the lunar orbit axis and its linear eccentricity is 4700 km or 1 , 2% smaller than the apogee distance .
Conversely, the distance from the center of the earth to the earth-moon center of gravity fluctuates by 1.2%, i.e. about ± 60 km in the rhythm of the anomalous (Keplerian) orbit period of the moon.
Vertical fluctuation
The fluctuation is less pronounced in the vertical direction than in the radial direction. The plane of the lunar orbit is about 5 ° to the ecliptic plane - the plane of the Earth-Sun Rotation - inclined . The moon moves on one half of its orbit around the earth above and during the other half below the ecliptic plane, the earth on the other side of the barycenter runs on the other side of the ecliptic plane; When running over the other half of the track, it is the other way around for both bodies. Because of the relatively small angle of inclination and the proximity of the earth to the center of the bary, this fluctuation of the earth is only a few hundred kilometers.