Two-body problem

In physics , a two-body problem is the task of calculating the movement of two bodies that only interact with one another without additional external influences. They form a two-body system. A typical case is the collision of two bodies, as long as all other possibly existing external forces can be neglected at least for a short time. Another typical case is a two-body system, in which the two bodies attract or repel one another with a force whose strength is inversely proportional to the square of their distance. Examples of such two-body systems are two astronomical objects (double stars, planet and sun, planet and moon, etc.) that are bound to one another by mutual gravitational fields and move around one another, or two charged particles that attract or repel one another in the mutual electrostatic field ( Proton and electron in the hydrogen atom , alpha particles when colliding with an atomic nucleus ).
In astronomy, the two-body problem is also known as the Kepler problem , because Johannes Kepler was the first to specify the exact form of motion for bound two-body systems in the three laws named after him . Its derivation is a standard task of classical mechanics , which was first solved by Isaac Newton .
The movements calculated according to classical mechanics also show up when additional external forces act, but these cancel each other out for each of the two bodies. An example is the friction-free sliding of two heavy bodies on a horizontal surface that is just neutralizing the weight forces, e.g. B. (approximately) when pair skating on ice or when two sliding or rolling bodies collide. Even if the two-body system is in a homogeneous gravity field, the laws of the two-body problem apply in its center of gravity.
With an electrostatic force field, the Kepler problem has the same solutions as with gravity. Since the applications here mainly relate to the interior of atoms (see Bohr-Sommerfeld's atomic model ), the quantum nature of the atomic particles must be taken into account. Therefore the quantum mechanical two-body problem has to be solved for a satisfactory representation . This shows in the case of two indistinguishable particles , e.g. B. when two electrons collide or two identical atomic nuclei, a fundamentally different behavior than according to classical mechanics.
The classic problem
Since only the two bodies (masses , locations ) interact, the equations of motion are called
According to the principle of relativity , the forces can only depend on the relative position of the bodies to one another. In addition, according to Newton's 3rd axiom, they are oppositely equal
and parallel to the connecting line:
- .
Transition to the equivalent one-body problem
You now calculate in relative and center of gravity coordinates (see figure):
- ( is the total mass.)
The vector describes the position of the 1st body relative to the 2nd, the vector is the position vector of the center of gravity or the barycenter of the system.
By adding suitable multiples of the above two equations of motion, we now get two decoupled equations of motion:
The first equation says that the center of mass describes a rectilinear uniform movement, as can also be deduced from the general principle of center of gravity . The second equation is rephrased to
in which
is called the reduced mass of the two-body problem. is always smaller than the smaller of the two masses, and approaches it when the larger mass tends towards infinity. This equation of motion says that the relative coordinate behaves as if a body of mass is moving in a stationary force field . This is the equivalent one-body problem. For all cases in which the strength of the force depends on a power of the distance , it was first solved by Newton.
Joint movement
After the one-body problem has been solved by the trajectory and the movement of the center of gravity is also known, you can convert back to the original coordinates:
Considered in the center of gravity system ( ), both bodies move around the center of gravity, are always facing each other and describe two curves similar to the curve, the size ratio of which is determined by the reciprocal mass ratio. By differentiating between and inserting twice you can see that the equation of motion for the first body
is fulfilled as if the body is in an effective force field
would move whose center remains stationary at the center of gravity and whose strength corresponds to the real force field at a greater distance determined by the mass ratio - the same for the other body.
If the center of gravity itself moves in a straight line and uniformly, the paths of the two bodies describe a kind of "snake curve" around the path of the center of gravity. This so-called tumbling movement allows z. B. an indirect observation of invisible companions of stars (such as exoplanets ).
Angular momentum conservation
Since the force according to Newton's 3rd axiom lies parallel to the connecting line , it is a central force and does not exert any torque on the rotating body, because this is given by the vector product of the radius vector and the force:
The angular momentum is therefore constant over time in terms of magnitude and direction. It is an integral of movement. Thus, the movement takes place in a fixed plane, because the vectors and are always in the plane perpendicular to .
From the constancy of the angular momentum, Kepler's second law or the law of areas follows, which is valid for every central force field.
In plane polar coordinates , the vectorial equation of motion of the one-body problem breaks down into two coupled ordinary differential equations:
The second of these equations shows once more the conservation of angular momentum , because
Energy conservation
For the Kepler problem in the narrower sense, the force is given by gravity:
If you use the definition of the angular momentum in polar coordinates to eliminate the angular velocity from the other differential equation , you get a law for the distance , the radial equation
This can be done after multiplying with and in the form
to be written. The three summands in this equation correspond in the order to the radial component of the kinetic energy, the angular component of the kinetic energy, which as centrifugal potential influences the radial movement like a potential energy, and the potential energy of the body in the external central potential. Together they result in his total energy
which according to the above equation is constant over time and is therefore also an integral of the movement. Of course, the total energy must be preserved simply because a gravitational field is a conservative field . See also the specific orbital energy article for a closer look at this.
Trajectory
If the values for the two integrals of the motion and are given, the equation of motion can be solved by first calculating the radial motion from the form of the energy integral (last equation in the section above) and then calculating the angular motion from the angular momentum integral. However, this path leads to equations that can be described as unrepresentative , since the shape of the path cannot be seen directly from them.
It is therefore common to first convert either the radial equation or the energy integral into a differential equation according to the angle instead of the time. So one takes as a function of and considers the derivative of with respect to the angle . Here the second way using the energy integral is presented.
With the energy equation from the previous section and by replacing with and with the help of the angular momentum equation, we get:
The trajectory that solves this equation is, if one uses the arbitrariness in the choice of the angle so that the greatest or smallest distance from the center is from the shape
whereby one can calculate by inserting that for the two parameters and must apply. This is the equation of a conic section with numerical eccentricity (where to choose).
If the total energy is negative, then and the movement is bound, i.e. i.e., there is a maximum distance (apoapsis) from the center. In this case, the orbit is an ellipse with one focus of the center, the major semi-axis of which is. This is Kepler's first law (theorem of ellipses). The fact that the trajectory of the bound state is always closed is a special case with radially symmetrical force fields, which otherwise only occurs with the harmonic oscillator , whose force field increases proportionally to the distance from the center.
If the total energy is positive, then and the orbit is a hyperbola with the smallest distance from the center. The borderline case with energy and is that of a parabola whose smallest distance from the center is.
Time parameters
In order to obtain the movement over time with a known path , the function can be determined from the angular momentum integral. This results in integration on a function that has yet to be inverted. A descriptive method to get the function is the Kepler equation found by Kepler . This method is based on Kepler's law of areas, i.e. That is, their physical basis is also the integral of angular momentum. The time dependency of the trajectory leads to the solution of a transcendent equation , except in special cases and so that the solution cannot be represented in closed form with the help of standard functions. Specifically, the solution to this equation is therefore determined using numerical methods.
The period of rotation of the body in an elliptical orbit, on the other hand, can be determined directly from the angular momentum integral. Since the area of the ellipse is and, in addition , is
This is exactly what Kepler's third law says.
The Kepler solution
Johannes Kepler neither set up nor solved the problem that was later named after him. But in the compact form of Kepler's three laws he described the resulting paths mathematically correct. Isaac Newton was able to publish the first solution in 1687. Kepler's laws formed a decisive touchstone for Newton's mechanics created by Newton. Strictly speaking, they are the solutions of the equivalent one-body problem , in which a source of gravity is fixed in space and attracts a single body without this having any effect on the source.
The solution to the problem is divided into the following parts:
- 1. and 2. Kepler's law (found 1599 to 1609, the ellipses - and the area theorem ) and
- 3. Kepler's Law (1619, published in World Harmony ).
- The Kepler equation .
Possible paths ( Kepler tracks ) are circles , ellipses , parabolas and hyperbolas in question. With circles and ellipses, the bodies are bound to one another like the planets to the sun. If the shape of the orbit is parabolic or hyperbolic, only one encounter takes place, as z. B. is the case with some comets .
The adjacent drawing shows various trajectories. They are characterized by their numerical eccentricity , which is a nonnegative real number. Have bound paths (circles and ellipses) , where the circle corresponds to an eccentricity . Larger eccentricities lead to open orbits (parabolas with ) and hyperbolas (with ). These open paths have not yet been mentioned by Kepler.
For a precise description of a heliocentric planetary system, however, Kepler's solution is not sufficient, because the mutual attraction of all celestial bodies, also discovered by Newton, is also effective in the planetary system. Therefore, the Kepler problem represents a physical idealization . In the solar system, as in many other astronomical systems, the influence of the other bodies is relatively small, so that the solution of the two-body problem provides a good approximation of the exact orbits. Therefore the solution of the two-body problem is the basis of modern celestial mechanics .
Inverse problem: orbit determination
With the solution of the two-body problem, it is possible to calculate the trajectory of two celestial bodies , which can be viewed with sufficient accuracy as a two-body system , if enough initial values are given. In celestial mechanics, however, one usually faces the inverse problem : The model parameters (initial values) are to be calculated from the observed orbit. With the methods presented above, the position of the celestial bodies can then be calculated for the (near) future if the disturbing influences are sufficiently small.
The number of initial values to be determined is always given by the original system of differential equations. Since it is a second order equation for the movement of two bodies in three-dimensional space, these are parameters. The form in which these twelve values appear, however, depends on the specific situation and the chosen procedure. In the “brute force” method of direct numerical integration of the initial system, for example, three values for the starting position and three values for the starting speed are given for each of the two bodies. If the analytical method presented above is selected, three starting position values and three starting speed values for the movement of the center of gravity are first sought. The remaining single center problem then requires a further six parameters, which are classically given by the path elements : two angles that define the position of the plane of motion in space (and thus the position of the angular momentum vector), one angle that describes the position of the path within this plane ( and thus the zero point of the polar angle ), as well as the major semi-axis and numerical eccentricity of the conic-shaped path (which together determine the energy and the amount of the angular momentum). In addition, the starting position of the revolving body must be specified as an angle or as a time reference by specifying the periapsis time. An alternative elegant method for specifying these six initial values is to specify two vectors that are constant over time: the angular momentum vector and the Laplace-Runge-Lenz vector . However, these two three-dimensional vectors determine not six, but only five of the path elements, since the vectors are necessarily perpendicular to one another. Therefore, the time reference must again be established by specifying the periapsis time, or a starting angle must be specified.
The most important methods for determining the orbital elements from the observation data go back to Isaac Newton, Pierre-Simon Laplace and Carl Friedrich Gauß .
Limits of the two-body solution
The two-body problem represents an idealization that seldom reflects the facts with sufficient accuracy in concrete situations. The only exceptions are true double stars without planets or other dark companions, whose components are far enough apart that tidal effects are negligible. Classical (non-quantum-theoretical) models of the hydrogen atom as well as radially symmetrical single-center scattering problems can be considered as two-body problems.
Multiple bodies
In almost all real situations there are more than two bodies in interaction with one another. The motion problem of several bodies cannot be solved in a similar way as it was presented here for two bodies. Even the three-body problem , i.e. the task of calculating the orbit when the interaction of a third body is taken into account, is usually not strictly solvable and can only be solved numerically in general. This difficulty naturally continues when solving multi-body problems with additional components. The only exceptions are highly symmetrical constellations in which, for example, the bodies form regular polygons, lie on a line or are extended in a shell-shaped manner around a center. Such arrangements find an important application in the study of the movement of small bodies which are located in one of the five Lagrangian points of a two-body system.
Deviation from spherical shape
Another problem is the deviation of one or both bodies from the spherical shape. Many astronomical bodies are only imprecisely described by a radially symmetrical mass distribution. In some cases the objects can be modeled much more precisely if one considers them to be flattened ellipsoids of revolution. This applies to many planets and stars, but also to spiral galaxies, which can be easily modeled as flat disks. If one of the two bodies is significantly smaller than the other, such a system can be described as an axially symmetric single-center problem, which is more general than the one described above, but is still accessible to a general solution. If both bodies are of comparable size and not flattened in the same direction, this path is also closed. In addition, tidal forces between the bodies can lead to dynamic deformations, as is often the case in close binary stars. These lead to a complex dynamic between the rotation of the individual bodies and the movement of the bodies around one another.
Perturbation theory
Nevertheless, the Kepler solution is the basis of all modern planetary theories (as well as the lunar theories and the motion theories of all other celestial bodies). The orbits of almost all natural objects in our solar system, most of the multiple stars and also of galaxies, are such that they can be described in a first approximation using the Kepler solution. The orbital elements of the Kepler orbits, which are determined from the initial conditions, are then no longer assumed to be constant, but are treated in terms of perturbation theory . The path elements that are valid at a certain point in time are then described as oscillating , since they determine the Kepler path that is currently as closely as possible to the real path .
Furthermore, the influences of the disruptive bodies on the two-body system can often be averaged over longer periods of time, which makes the description of the problem more symmetrical. Such influences lead z. T. to time-constant or periodic changes in the path elements. Examples of such phenomena are e.g. B. the uniform rotation of the apsidal line , i.e. the position of the Kepler orbit in the plane of the orbit , and the uniform shifting of the orbit nodes around an invariant plane (the Laplace plane ). In the lunar theory, further examples of such periodic disturbances are evection and variation .
Two-body systems in general relativity
The modern theory of gravity is described in the general theory of relativity (GTR). If the masses of the two bodies are sufficiently small, the distances to each other relatively large and the speeds of the bodies far below the speed of light , the system can be described by the Newtonian limit case of the theory. In other words: The solution sketched above within Newton's theory of gravity offers a very good approximate solution. However, if the conditions for the validity of the borderline case are not met or the requirements for accuracy are very high, the problem must be solved within the full ART - a task that turns out to be much more complicated.
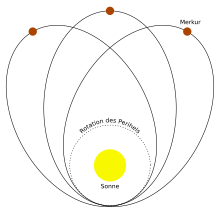
In the simplest case, which fortunately has many uses, one of the two bodies has a much greater mass than the other. It is then justified to regard the small object as a test object in the field of the large object, i.e. that is, the small body has no noticeable effect on the large one. The problem can then be described as a general relativistic single-center problem, analogous to Newton's theory . This problem also proves to be easy to analyze in GTR due to the radial symmetry. In a similar form to that described above, integrals of the motion can be found. However, the analysis leads to a radial equation that contains an additional term compared to Newton's theory, which means that the orbits are not closed even with negative total energy . Instead, the orbits are rosette orbits, as is the case for two-body systems with other laws of force than Newton's . This effect has gained fame as it makes it possible to explain the additional perihelion rotation of Mercury.
The general relativistic two-body problem in general, i.e. with two bodies that interact with one another, is much more complicated. Since the presence of the two masses changes the space-time structure itself, concepts such as center of mass, total energy, angular momentum are no longer applicable. It is therefore not possible to reduce the problem to a single center problem. In addition, the influence on space-time is anchored in the mathematical structure because the problem is not described by ordinary differential equations , but by partial differential equations . The nonlinear structure of these equations makes solving the equations even with numerical methods problematic. In a heuristic approach, one can generally try to adopt the classical concepts approximately. This description leads to effects such as the radiation of gravitational waves and an associated "loss of angular momentum". The orbits of the bodies then described spiral trajectories around a common “center of gravity”, which become closer and closer as the orbital time becomes shorter. The exact description of these phenomena in the context of a post-Newtonian approximation is controversial due to the unexplained convergence properties of the approximations.
Footnotes
-
↑ In most cases the substitution is also carried out so that the following differential equation is obtained:
- ↑ The reason for this is not that a general closed solution has not yet been found. Rather, it is a fundamental, provable property of the structure of the differential equation system that does not allow the existence of a closed solution.
- ↑ As in Newton's case, the existence of the “integrals”, i.e. H. of the conserved quantities of motion, justifiable from the general Noether theorem .
- ↑ Since there are no symmetries, the existence of conserved quantities cannot be derived from the general Noether theorem.
Individual evidence
- ^ Isaac Newton: The Mathematical Principles of Physics. Translated and edited by Volkmar Schüller, de Gruyter, Berlin (among others) 1999, ISBN 3-11-016105-2 , (p. 184 ff., Proposition LVII to LXIII).
- ^ Clifford M. Will : Theory and Experiment in Gravitational Physics. Revised edition. Cambridge University Press, Cambridge et al. 1993, ISBN 0-521-43973-6 .
- ^ Albert Einstein, Leopold Infeld : On the Motion of Particles in General Relativity Theory. In: Canadian Journal of Mathematics. Vol. 1, 1949, pp. 209-241, doi : 10.4153 / CJM-1949-020-8 .
literature
- Andreas Guthmann: Introduction to celestial mechanics and ephemeris calculus. BI-Wissenschaftsverlag, Mannheim et al. 1994, ISBN 3-411-17051-4 .
- Archie E. Roy: Orbital Motion. 3rd edition, student text. Adam Hilger, Bristol et al. 1988, ISBN 0-85274-228-2 .
- Walter Thirring : Textbook of Mathematical Physics. Volume 1: Classical Dynamic Systems. 2nd, revised edition. Springer, Vienna et al. 1988, ISBN 3-211-82089-2 , (Chapter 4.2).
- Hannu Kartutunen, Pekka Kröger, Heikki Oja, Markku Poutannen, Karl J. Donner (eds.): Fundamental Astronomy. Springer, Wien et al. 1987, ISBN 3-540-17264-5 , (chapter 7).