Barycenter
With barycenter (from ancient Greek βαρύς Barys , German , heavy weight, burdensome ' , also center of mass ) is called in the geometry of the weighted center of gravity (more precisely, the center of mass) multiple (point) mass, after in the center of gravity principle , the inertial force "attacks" . In celestial mechanics , the weighting factors of the points are their masses or, in the case of continuous mass distribution, their densities .
In a homogeneous external gravitational field , the barycentre is also the center of gravity , i.e. H. the average point of application of the forces acting on the points of the external forces. In the inhomogeneous field, the barycentre and the gravitational center are no longer identical, in this case a torque can arise.
The common gravitational field of spherically symmetrical mass distributions acts as if the whole mass were concentrated in the barycentre, see Newton's shell theorem or Birkhoff's theorem . For other mass distributions such as the following multibody systems, this only applies approximately at great distances.
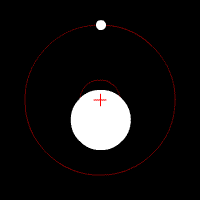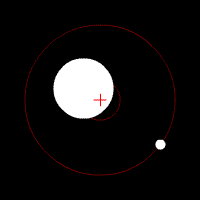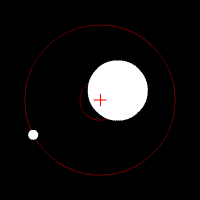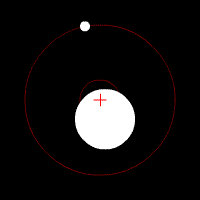
Barycentre in the two-body system
Due to the linearity of the averaging , the barycentre of several bodies can be calculated as the weighted average of their respective barycentre. For a system made up of two spherically symmetrical bodies it follows that the common barycentre lies on the line connecting the spherical centers, with the following distance from center 1:
The variables are:
- - the distance of the barycentre from the center of the body 1
- - the distance between the two centers of the body
- and - the masses of the two bodies.
Examples
Earth and moon
For earth and moon, the barycentre lies just inside the earth, see earth-moon center of gravity .
Pluto and Charon
The barycenter of the Pluto - Charon system is due to the relatively small mass ratio of approx. 8/1 approx. 1200 km above Pluto's surface. This is circled by Charon and Pluto.
Solar system
The position of the barycentre of the solar system depends mainly on the position of Jupiter and Saturn to each other, see major conjunction . The two giant planets have 0.10 and 0.03 percent of the mass of the sun , so they influence the barycentre around this fraction of their orbital half-axes (around 740,000 and 410,000 km). Since the solar radius is 696,000 km, the barycentre is sometimes inside and sometimes outside the solar surface , a maximum of 2.098 solar radii from the center of the sun.
The barycenter of the solar system is not only the geometric origin of the barycentric ecliptical coordinate system , but also the location for a virtual atomic clock that defines the Temps atomique barymetrique (TAB), see gravitational time dilation .
Barycentric coordinates
In a homogeneous gravitational field or without external forces, the following applies: A non-rotating reference system in which the barycentre rests is an inertial system , i.e. particularly suitable for describing the dynamics of the system, see barycentric coordinates . So is in many earth models , z. B. WGS 84 , the barycenter of the earth selected as the zero point of the coordinates .
Individual evidence
- ^ Wilhelm Pape , Max Sengebusch (arrangement): Concise dictionary of the Greek language. 3rd edition, 6th impression, Vieweg & Sohn, Braunschweig 1914. 1914, accessed on July 28, 2020 .
- ↑ Ilka Agricola, Thomas Friedrich: Elementarge Geometry: Expertise for studies and mathematics lessons. 4th, revised edition, Springer Spectrum, Wiesbaden 2015, ISBN 978-3-658-06730-4 , doi : 10.1007 / 978-3-658-06731-1 , limited preview in the Google book search.
- ^ Jean Meeus: Mathematical astronomy morsels . Richmond, Va. 2009, ISBN 978-0-943396-92-7 , pp. 165 .