Barycentric coordinates

This article describes barycentric coordinates in geometry . In astronomy , coordinates are referred to as barycentric, which refer to a center of gravity of a system of celestial bodies , cf. also astronomical coordinate systems .

The barycentric coordinates of a point (blue) are the proportions of three masses in the corners of a triangle (red), whose center of gravity (center of mass) is the point . In this example has the barycentric coordinates . ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle (2:4:5)}$

The connection between physics and geometry is provided by the equation of the law of levers : According to this, the ratio of the masses is equal to the ratio of the distances that describe the position of the center of gravity. ${\displaystyle m_{1},m_{2}}$ ${\displaystyle l_{2},l_{1}}$

Barycentric coordinates (also homogeneous barycentric coordinates ) are used in linear algebra and in geometry to describe the position of points in relation to a given segment , a given triangle , a given tetrahedron or, more generally, a given simplex .

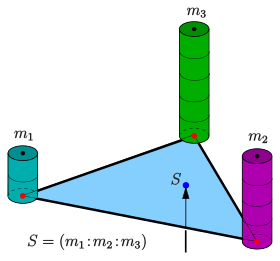
The plane barycentric coordinates of a point can be imagined as the ratios of three masses , which are located in the corners of a given triangle and whose center of gravity is (see picture). Since it only depends on the circumstances, you write . If all masses are the same, the geometric center of gravity is the triangle and has the barycentric coordinates . The barycentric coordinates get their geometric meaning through the following properties: In the 1-dimensional the mass ratio is equal to a ratio of partial distances (see 2nd picture), in the 2-dimensional the mass ratios are equal to the area ratios of partial triangles (see section Relationship to triangular areas and trilinear areas Coordinates ). ${\displaystyle S}$ ${\displaystyle m_{1},m_{2},m_{3}}$ ${\displaystyle S}$ ${\displaystyle (m_{1}:m_{2}:m_{3})}$ ${\displaystyle S}$ ${\displaystyle (1:1:1)}$

Barycentric coordinates were first introduced by AF Möbius in 1827 in his book Der Baryzentrische Calcul . They are a special case of homogeneous coordinates . A major difference to the usual homogeneous coordinates, e.g. B. in the plane, the description of the distance line is by the equation instead of by . ${\displaystyle x_{1}+x_{2}+x_{3}=0}$ ${\displaystyle x_{3}=0}$

In triangular geometry in particular , the barycentric coordinates play an important role alongside the trilinear coordinates . They are a suitable tool wherever relations between distances are involved, as for example in Ceva's theorem . But not only in geometry, but also in the field of computer-aided design , they are used to create triangular surfaces, the triangular Bézier surfaces .

In the section on introducing barycentric coordinates , the coordinates are marked with in order to remind you of their relation to masses and their center of gravity, which is often a help. Only in the section General barycentric coordinates are the common mathematical terms used. ${\displaystyle (m_{1}:m_{2}),(m_{1}:m_{2}:m_{3})}$

Introduction of barycentric coordinates

2 masses on a straight line

Center of gravity of two masses

The center of gravity of two masses placed on the -axis at the points is the point at which the mass must be attached so that it causes the same torque with respect to any point. Regarding of the zero point must therefore apply: ${\displaystyle m_{1},m_{2}}$ ${\displaystyle x}$ ${\displaystyle x_{1},x_{2}}$ ${\displaystyle x_{s}}$ ${\displaystyle m_{1}+m_{2}}$

(G1) ${\displaystyle \ (m_{1}+m_{2})x_{s}=m_{1}x_{1}+m_{2}x_{2}}$

Dissolving gives:

(S1) ${\displaystyle \ x_{s}={\frac {m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}}}$

Properties of the center of gravity

1. The position of the center of gravity does not depend on the random choice of the zero point and a scaling.
2. The location of the center of gravity depends only on the ratio . That means: the masses have the same center of gravity. ${\displaystyle m_{1}:m_{2}}$ ${\displaystyle cm_{1},cm_{2}}$
3. If one allows negative masses, e.g. B. , it results for the total mass and . ${\displaystyle m_{1}=1,m_{2}=-1+{\tfrac {1}{n}}}$ ${\displaystyle n\to \infty }$ ${\displaystyle m_{1}+m_{2}=0}$ ${\displaystyle x_{s}=\infty }$

Barycentric coordinates of a straight line

Barycentric coordinates on a straight line (below). The midpoint of the line has the barycentric coordinates ${\displaystyle X_{1},X_{2}}$ ${\displaystyle (1:1)=({\tfrac {1}{2}}:{\tfrac {1}{2}})}$

The relation of a center of gravity to two given masses allows any point of the -axis to be understood as the center of gravity of two masses placed in . However, this assignment is not clear. The uniqueness can be enforced with the requirement . ${\displaystyle x_{s}}$ ${\displaystyle x}$ ${\displaystyle x_{1},x_{2}}$ ${\displaystyle m_{1},m_{2}}$ ${\displaystyle \;m_{1}+m_{2}=1\;}$

Pairs of masses at the fixed points can be understood as homogeneous coordinates of a point (the center of gravity of the masses) of the axis. Because of this relationship, these coordinates are called barycentric coordinates of the point . The point or has the homogeneous coordinates or . The following applies to the far point . It has the barycentric coordinates . Note: In the usual (not barycentric) homogeneous coordination, the far point is described by (1: 0). ${\displaystyle m_{1},m_{2}}$ ${\displaystyle x_{1},x_{2}}$ ${\displaystyle (m_{1}:m_{2})}$ ${\displaystyle x_{s}}$ ${\displaystyle x}$ ${\displaystyle x_{s}}$ ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$ ${\displaystyle (1:0)}$ ${\displaystyle (0:1)}$ ${\displaystyle \infty }$ ${\displaystyle \;m_{1}+m_{2}=0\;}$ ${\displaystyle (1:-1)}$

If the uniqueness by the equation

(N1) ${\displaystyle \quad m_{1}+m_{2}=1}$

is forced, one speaks of normalized barycentric coordinates.

Is a point given, we obtain its barycentric coordinates by solving the equilibrium equation (G1) according to , which is not possible as clearly under-determined system of linear equations: ${\displaystyle x_{s}}$ ${\displaystyle m_{1},m_{2}}$

Barycentric coordinates as a ratio of distances

(B1) ${\displaystyle \;(m_{1}:m_{2})=(x_{2}-x_{s}:x_{s}-x_{1})=(l_{\color {red}2}:l_{\color {red}1})}$

It is this simple connection, the barycentric coordinates with ratios of distances is the reason for their importance in the triangular geometry. ${\displaystyle \;l_{1}=x_{s}-x_{1},\;l_{2}=x_{2}-x_{s}\;.}$

In the normalized case for equation (G1) , the normalization equation (N1) added taken, whereby the LGS for uniquely. Solution with Cramer's rule delivers ${\displaystyle m_{1},m_{2}}$

${\displaystyle m_{1}={\frac {x_{2}-x_{s}}{x_{2}-x_{1}}},\ m_{2}={\frac {x_{s}-x_{1}}{x_{2}-x_{1}}}}$

and thus the normalized barycentric coordinates

(NB1) ${\displaystyle \ {\big (}{\frac {x_{2}-x_{s}}{x_{2}-x_{1}}}\;:\;{\frac {x_{s}-x_{1}}{x_{2}-x_{1}}}{\big )}={\big (}{\frac {l_{2}}{l_{1}+l_{2}}}:{\frac {l_{1}}{l_{1}+l_{2}}}{\big )}\;.}$

The center of the points has the barycentric coordinates and in a standardized representation ${\displaystyle {\tfrac {x_{1}+x_{2}}{2}}}$ ${\displaystyle x_{1},x_{2}}$ ${\displaystyle (1:1)}$ ${\displaystyle ({\tfrac {1}{2}}:{\tfrac {1}{2}})\;.}$

3 masses in one plane

If three masses are placed in the corners of a triangle , the equations of equilibrium for the torques are around the coordinate axes ${\displaystyle \;X_{1}=(x_{1},y_{1}),\;X_{2}=(x_{2},y_{2}),\;X_{3}=(x_{3},y_{3}),\;}$ ${\displaystyle m_{1},m_{2},m_{3}}$

(G) ${\displaystyle \ {\begin{array}{c}(m_{1}+m_{2}+m_{3})x_{s}=m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}\\(m_{1}+m_{2}+m_{3})y_{s}=m_{1}y_{1}+m_{2}y_{2}+m_{3}y_{3}\end{array}}}$

Barycentric coordinates in the plane: The masses are in the points . The purple parallel lines have the given equations. Their common far point has the coordinates ${\displaystyle X_{1},X_{2},X_{3}}$ ${\displaystyle m_{1},m_{2},m_{3}}$ ${\displaystyle (1:-1:0).}$

and the center of gravity has the coordinates

(S) ${\displaystyle \ {\begin{array}{c}x_{s}=\displaystyle {\frac {m_{1}x_{1}+m_{2}x_{2}+m_{3}x_{3}}{m_{1}+m_{2}+m_{3}}}\\y_{s}=\displaystyle {\frac {m_{1}y_{1}+m_{2}y_{2}+m_{3}y_{3}}{m_{1}+m_{2}+m_{3}}}.\end{array}}}$

Barycentric coordinates of a plane

As in the 1-dimensional case, the masses can be understood as (homogeneous) barycentric coordinates of points in the plane. ${\displaystyle (m_{1}:m_{2}:m_{3})}$

• The corners of the triangle have the homogeneous coordinates

${\displaystyle X_{1}=(1\!:\!0\!:\!0),\;X_{2}=(0\!:\!1\!:\!0),\;X_{3}=(0\!:\!0\!:\!1)\;}$.

• The straight line through the points is described by the equation and has the far point . ... ${\displaystyle X_{1},X_{2}}$ ${\displaystyle m_{3}=0}$ ${\displaystyle (1:-1:0)}$
• The distance line is determined by the equation . ${\displaystyle \;m_{1}+m_{2}+m_{3}=0\;}$
• Any straight line is described by an equation (see homogeneous coordinates). ${\displaystyle \;am_{1}+bm_{2}+cm_{3}=0\;}$
• Three straight lines have a point in common, if ${\displaystyle \;a_{1}m_{1}+b_{1}m_{2}+c_{1}m_{3}=0,\;a_{2}m_{1}+b_{2}m_{2}+c_{2}m_{3}=0,\;a_{3}m_{1}+b_{3}m_{2}+c_{3}m_{3}=0\;\ }$

${\displaystyle \qquad \quad \left|{\begin{matrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{matrix}}\right|=0}$.

• Two lines are parallel if they intersect on the distant line, i.e. i.e. if ${\displaystyle \;a_{1}m_{1}+b_{1}m_{2}+c_{1}m_{3}=0,\;a_{2}m_{1}+b_{2}m_{2}+c_{2}m_{3}=0}$

${\displaystyle \qquad \quad \left|{\begin{matrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\1&1&1\end{matrix}}\right|=0}$.

• Three points , and are on a straight line if and only if ${\displaystyle (m_{1}:m_{2}:m_{3})}$ ${\displaystyle (m'_{1}:m'_{2}:m'_{3})}$ ${\displaystyle (m''_{1}:m''_{2}:m''_{3})}$

${\displaystyle \qquad \quad \left|{\begin{matrix}m_{1}&m_{2}&m_{3}\\m'_{1}&m'_{2}&m'_{3}\\m''_{1}&m''_{2}&m''_{3}\end{matrix}}\right|=0.}$

• This results in the equation of a straight line through two given points in determinant form: ${\displaystyle \;am_{1}+bm_{2}+cm_{3}=0\;}$ ${\displaystyle (u_{1}:u_{2}:u_{3}),(v_{1}:v_{2}:v_{3})}$

${\displaystyle \qquad \quad \left|{\begin{matrix}m_{1}&m_{2}&m_{3}\\u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\end{matrix}}\right|=0}$

• Barycentric coordinates of a point are obtained by solving the two equilibrium equations (G) (underdetermined linear system of equations) . Take the normalization equation ${\displaystyle S=({\color {red}x_{s}},{\color {red}y_{s}})}$ ${\displaystyle m_{1},m_{2},m_{3}}$

(N) ${\displaystyle \quad m_{1}+m_{2}+m_{3}=1}$

In addition, the LGS is clear and can be solved with the help of Cramer's rule. It results:

${\displaystyle S=(x_{s},y_{s}),\;X_{i}=(x_{i},y_{i})}$

(NB) ${\displaystyle \qquad {\begin{array}{l}m_{1}=\displaystyle {\frac {(x_{2}-{\color {red}x_{s}})(y_{3}-{\color {red}y_{s}})-(x_{3}-{\color {red}x_{s}})(y_{2}-{\color {red}y_{s}})}{(x_{2}-x_{1})(y_{3}-y_{2})-(y_{2}-y_{1})(x_{3}-x_{2})}}\\m_{2}=\displaystyle {\frac {(x_{3}-{\color {red}x_{s}})(y_{1}-{\color {red}y_{s}})-(x_{1}-{\color {red}x_{s}})(y_{3}-{\color {red}y_{s}})}{(x_{2}-x_{1})(y_{3}-y_{2})-(y_{2}-y_{1})(x_{3}-x_{2})}}\\m_{3}=\displaystyle {\frac {(x_{1}-{\color {red}x_{s}})(y_{2}-{\color {red}y_{s}})-(x_{2}-{\color {red}x_{s}})(y_{1}-{\color {red}y_{s}})}{(x_{2}-x_{1})(y_{3}-y_{2})-(y_{2}-y_{1})(x_{3}-x_{2})}}\\\end{array}}}$

(Because of this , it is sufficient to calculate two of the three fractions.) ${\displaystyle m_{1}+m_{2}+m_{3}=1}$

All counters can be written as determinants. If the normalization is not used, the common denominator of the barycentric coordinates can be omitted: ${\displaystyle 2\times 2}$

${\displaystyle (m_{1}:m_{2}:m_{3})={\Big (}\left|{\begin{array}{l}x_{2}\!-\!{\color {red}x_{s}}&x_{3}\!-\!{\color {red}x_{s}}\\y_{2}\!-\!{\color {red}y_{2}}&y_{3}\!-\!{\color {red}y_{s}}\\\end{array}}\right|:\left|{\begin{array}{l}x_{3}\!-\!{\color {red}x_{s}}&x_{1}\!-\!{\color {red}x_{s}}\\y_{3}\!-\!{\color {red}y_{s}}&y_{1}\!-\!{\color {red}y_{s}}\\\end{array}}\right|:\left|{\begin{array}{l}x_{1}\!-\!{\color {red}x_{s}}&x_{2}\!-\!{\color {red}x_{s}}\\y_{1}\!-\!{\color {red}y_{s}}&y_{2}\!-\!{\color {red}y_{s}}\\\end{array}}\right|{\Big )}}$

Multiplying each determinant with , caused the oriented surfaces of the sub-triangles , , (see the next section relationship with triangular surfaces ). The following applies: ${\displaystyle {\tfrac {1}{2}}}$ ${\displaystyle \Delta _{1},\Delta _{2},\Delta _{3}}$ ${\displaystyle X_{2}X_{3}S}$ ${\displaystyle X_{1}X_{3}S}$ ${\displaystyle X_{1}X_{2}S}$

(BF) ${\displaystyle \qquad (m_{1}:m_{2}:m_{3})=(\Delta _{1}:\Delta _{2}:\Delta _{3})}$

Special case: coordinate triangle:

For the special right-angled triangle as a reference triangle , a point has the simple barycentric coordinates . ${\displaystyle \;X_{3}=(0,0),X_{1}=(1,0),X_{2}=(0,1)\;}$ ${\displaystyle (x,y)}$ ${\displaystyle (x:y:1-x-y)}$

Relationship to triangle faces and trilinear coordinates

The torque around the straight line through from with lever is equal to the moment of the total mass at the point with lever , since the levers of the masses are equal to 0 during this rotation ${\displaystyle X_{1},X_{2}}$ ${\displaystyle m_{3}}$ ${\displaystyle h_{3}}$ ${\displaystyle S}$ ${\displaystyle d_{3}}$ ${\displaystyle m_{1},m_{2}}$

In this section, the formula (BF) derived in the previous section is physically derived somewhat more simply:

If the torques around the triangle sides are equal to the total mass in the center of gravity and the individual masses, the following equations result (see figure, ): ${\displaystyle S}$ ${\displaystyle i=1,2,3}$

(GS) ${\displaystyle \ m_{i}h_{i}=(m_{1}+m_{2}+m_{3})\;d_{i}}$

The three heights of the triangle and the distances between the center of gravity and the individual sides of the triangle mean . If you multiply each equation by the corresponding half of the triangle side, the triangular area is the factor on the left in each equation and the areas of the partial triangles on the right (green in the picture): ${\displaystyle h_{1},h_{2},h_{3}}$ ${\displaystyle d_{1},d_{2},d_{3}}$ ${\displaystyle \Delta }$ ${\displaystyle \Delta _{i}}$

(DF) ${\displaystyle \ m_{i}\Delta =(m_{1}+m_{2}+m_{3})\;\Delta _{i}}$

From this you can see

(BF) ${\displaystyle \ (m_{1}:m_{2}:m_{3})=(\Delta _{1}:\Delta _{2}:\Delta _{3})}$

(BT) ${\displaystyle \ (m_{1}:m_{2}:m_{3})=(s_{1}d_{1}:s_{2}d_{2}:s_{3}d_{3})\ ,}$

where are the lengths of the sides of the triangle. So that negative coordinates (for points outside the given triangle) can also occur, the triangular areas or distances must be oriented . ${\displaystyle s_{1}=|X_{2}X_{3}|,\dotsc }$

The relationship (BT) shows the simple connection between the barycentric coordinates and the trilinear coordinates of a point. For an equilateral triangle , the barycentric and trilinear coordinates are the same. ${\displaystyle (d_{1}:d_{2}:d_{3})}$

Special case of geometric center of gravity

${\displaystyle S}$is the geometric center of gravity when all masses are equal. From (GS) and (BF) it follows

${\displaystyle d_{i}={\tfrac {1}{3}}h_{i}\quad }$ and ${\displaystyle \quad \Delta _{1}=\Delta _{2}=\Delta _{3}\ .}$

(See also Geometric Center of Gravity .)

Special case, inscribed center

For the inscribed circle of the triangle applies (Inkreisradius) and thus has the incentre the barycentric coordinates and because applies ${\displaystyle d_{i}=r}$ ${\displaystyle (s_{1}:s_{2}:s_{3})}$ ${\displaystyle \;\Delta =\Delta _{1}+\Delta _{2}+\Delta _{3}={\tfrac {1}{2}}(s_{1}+s_{2}+s_{3})r\;}$ ${\displaystyle \;r={\tfrac {2\Delta }{s_{1}+s_{2}+s_{3}}}\;.}$

Application: Ceva's theorem

Theorem of Ceva

Theorem of Ceva

If P is a point within the triangle and the intersection of the straight line with the side (see figure), then applies ${\displaystyle X_{1},X_{2},X_{3}}$ ${\displaystyle P_{i}}$ ${\displaystyle {\overline {PX_{i}}}}$ ${\displaystyle X_{j}X_{k}}$

${\displaystyle {\frac {|X_{2}P_{1}|}{|X_{3}P_{1}|}}\cdot {\frac {|X_{3}P_{2}|}{|X_{1}P_{2}|}}\cdot {\frac {|X_{1}P_{3}|}{|X_{2}P_{3}|}}=1\;.}$

proof

With the points in barycentric coordinates:

${\displaystyle X_{1}=(1:0:0),\;X_{2}=(0:1:0),\;X_{3}=(0:0:1)}$

${\displaystyle P=(\mu _{1}:\mu _{2}:\mu _{3})}$

results in the equation of the straight line (see above.) to and thus the intersection with the straight line (whose equation is) . From B1 one obtains. Carrying out these considerations for the straight line results in ${\displaystyle {\overline {X_{1}P}}}$ ${\displaystyle \;\mu _{3}m_{2}-\mu _{2}m_{3}=0\;}$ ${\displaystyle {\overline {X_{2}X_{3}}}}$ ${\displaystyle m_{1}=0}$ ${\displaystyle P_{1}=(0:\mu _{2}:\mu _{3})}$ ${\displaystyle |X_{2}P_{1}|:|X_{3}P_{1}|=\mu _{3}:\mu _{2}\;.}$ ${\displaystyle {\overline {X_{3}X_{1}}},{\overline {X_{3}X_{1}}}}$

${\displaystyle {\frac {|X_{2}P_{1}|}{|X_{3}P_{1}|}}\cdot {\frac {|X_{3}P_{2}|}{|X_{1}P_{2}|}}\cdot {\frac {|X_{1}P_{3}|}{|X_{2}P_{3}|}}={\frac {\mu _{3}}{\mu _{2}}}\cdot {\frac {\mu _{1}}{\mu _{3}}}\cdot {\frac {\mu _{2}}{\mu _{1}}}=1\;.}$

General definition of barycentric coordinates

definition

Let be the corners of a simplex in an affine space A. If for a point in A ${\displaystyle \mathbf {x} _{1},\dotsc ,\mathbf {x} _{n}}$ ${\displaystyle \mathbf {p} }$

${\displaystyle (a_{1}+\dotsb +a_{n})\mathbf {p} =a_{1}\,\mathbf {x} _{1}+\dotsb +a_{n}\,\mathbf {x} _{n}}$

holds and at least one of the numbers does not vanish, then the coefficients are said to be the barycentric coordinates of with respect to the vertices . The corners themselves have the coordinates . Barycentric coordinates are not unique: for every c not equal to zero there are also ( ) barycentric coordinates of . ${\displaystyle a_{1},\dotsc ,a_{n}}$ ${\displaystyle (a_{1}:\dotsc :a_{n}}$ ${\displaystyle \mathbf {p} }$ ${\displaystyle \mathbf {x} _{1},\dotsc ,\mathbf {x} _{n}}$ ${\displaystyle \mathbf {x} _{1}=(1:0:0:\ldots :0),\mathbf {x} _{2}=(0:1:0:\dotsc :0)\dotsc ,\mathbf {x} _{n}=(0:0:0:\dotsc :1)}$ ${\displaystyle ca_{1}:\dotsc :ca_{n}}$ ${\displaystyle \mathbf {p} }$

If the coordinates also fulfill the normalization condition ${\displaystyle (a_{1}:\dotsc :a_{n})}$

${\displaystyle a_{1}+\dotsb +a_{n}=1}$,

one speaks of normalized barycentric coordinates. These are clearly defined. Normalized barycentric coordinates can be easily determined by dividing each individual coordinate by the sum of the coordinates.

Note: The terms are not used uniformly. Many authors speak of barycentric coordinates only if the normalization condition is fulfilled.

If the coordinates are positive, the point lies in the convex hull of , i.e. in the simplex with these corner points. The representation of a point within a convex hull as the sum of corner points of a simplex is called an affine combination or barycentric combination . ${\displaystyle \mathbf {p} }$ ${\displaystyle \mathbf {x} _{1},\dotsc ,\mathbf {x} _{n}}$

How to get out of the switch

${\displaystyle \mathbf {p} ={\frac {a_{1}\mathbf {x} _{1}+\dotsb +a_{n}\mathbf {x} _{n}}{a_{1}+\dotsb +a_{n}}}}$

the definition equation sees, is the center of mass (the barycenter ) of an arrangement of masses at the corner points of the simplex . This is the origin of the term barycentric. ${\displaystyle \mathbf {p} }$ ${\displaystyle a_{1},\dotsc ,a_{n}}$ ${\displaystyle \mathbf {x} _{1},\dotsc ,\mathbf {x} _{n}}$

Example n = 4 (tetrahedron)

In 3-dimensional space, a simplex is a tetrahedron with the corners . In order to determine the barycentric coordinates of a point with regard to the given Tedrahedron, one has to use the linear system of equations, analogous to the 2-dimensional case (triangle) ${\displaystyle \mathbf {x} _{1},\mathbf {x} _{2},\mathbf {x} _{3},\mathbf {x} _{4}}$ ${\displaystyle \mathbf {p} }$

${\displaystyle (a_{1}+a_{2}+a_{3}+a_{4})\mathbf {p} =a_{1}\mathbf {x} _{1}+a_{2}\mathbf {x} _{2}+a_{3}\mathbf {x} _{3}+a_{4}\mathbf {x} _{4}}$

for solve. As in the case above, the normalization equation is added and the LGS is solved with the help of Cramer's rule. With the abbreviations ${\displaystyle a_{1},a_{2},a_{3},a_{4}}$ ${\displaystyle a_{1}+a_{2}+a_{3}+a_{4}=1}$

${\displaystyle V_{1}={\frac {1}{6}}\det(\mathbf {x} _{2}-\mathbf {p} ,\mathbf {x} _{3}-\mathbf {p} ,\mathbf {x} _{4}-\mathbf {p} ),\quad V_{2}={\frac {1}{6}}\det(\mathbf {x} _{3}-\mathbf {p} ,\mathbf {x} _{4}-\mathbf {p} ,\mathbf {x} _{1}-\mathbf {p} ),}$

${\displaystyle V_{3}={\frac {1}{6}}\det(\mathbf {x} _{4}-\mathbf {p} ,\mathbf {x} _{1}-\mathbf {p} ,\mathbf {x} _{2}-\mathbf {p} ),\quad V_{4}={\frac {1}{6}}\det(\mathbf {x} _{1}-\mathbf {p} ,\mathbf {x} _{2}-\mathbf {p} ,\mathbf {x} _{3}-\mathbf {p} )}$

Barycentric coordinates with respect to a tetrahedron (in space)

one obtains for the barycentric coordinates of : ${\displaystyle \mathbf {p} }$

${\displaystyle (a_{1}:a_{2}:a_{3}:a_{4})=(V_{1}:V_{2}:V_{3}:V_{4})}$

Here is the volume of the partial tetrahedron that arises from the given tetrahedron by replacing it with (see picture). If the base area (side surface of the Tedrahedron) and the height of the -th partial tetrahedron, then applies and ${\displaystyle V_{i}}$ ${\displaystyle \mathbf {x} _{i}}$ ${\displaystyle \mathbf {p} }$ ${\displaystyle \Delta _{i}}$ ${\displaystyle d_{i}}$ ${\displaystyle i}$ ${\displaystyle V_{i}={\tfrac {1}{3}}\Delta _{i}d_{i}}$

• ${\displaystyle (a_{1}:a_{2}:a_{3}:a_{4})=(\Delta _{1}d_{1}:\Delta _{2}d_{2}:\Delta _{3}d_{3}:\Delta _{4}d_{4})\ .}$

Special case of geometric center of gravity

The geometric center of gravity has the barycentric coordinates . So is ${\displaystyle (1:1:1:1)}$

${\displaystyle V_{i}={\frac {1}{3}}\Delta _{i}d_{i}={\frac {1}{4}}V={\frac {1}{4}}{\frac {1}{3}}\Delta _{i}h_{i}\;,}$

where is the volume of the given tetrahedron and the height of the -th point above the -th side triangle (see picture). So: ${\displaystyle V}$ ${\displaystyle h_{i}}$ ${\displaystyle i}$ ${\displaystyle i}$

${\displaystyle d_{i}={\frac {h_{i}}{4}}}$

(Compare the corresponding statement in the above case.)

The following obvious property can also be easily checked with barycentric coordinates:

The straight line through a corner and the geometric center of gravity intersects the triangle opposite the corner in its center of gravity.

Special case of the center of the sphere

For the center of the incugel is (radius of the incugel) and thus ${\displaystyle d_{i}=r}$

${\displaystyle (a_{1}:a_{2}:a_{3}:a_{4})=(\Delta _{1}:\Delta _{2}:\Delta _{3}:\Delta _{4})\ }$ and

${\displaystyle r={\frac {3V}{\Delta _{1}+\Delta _{2}+\Delta _{3}+\Delta _{4}}}\;,}$

where is the volume of the given tetrahedron. ${\displaystyle V=V_{1}+V_{2}+V_{3}+V_{4}}$

Generalized barycentric coordinates

Barycentric coordinates that are defined with reference to a polytope rather than a simplex are called generalized barycentric coordinates . It is also required here that the equation ${\displaystyle (a_{1},\dotsc ,a_{n})}$

${\displaystyle (a_{1}+\dotsb +a_{n})\mathbf {p} =a_{1}\,\mathbf {x} _{1}+\dotsb +a_{n}\,\mathbf {x} _{n}}$

is fulfilled, where here are the corner points of the given polytope. The definition is therefore formally unchanged, but a simplex with corner points must be contained in a vector space with a dimension of at least , while polytopes can also be embedded in vector spaces of lower dimension. The simplest example is a square in the plane. As a consequence, even the normalized generalized barycentric coordinates for a polytope are in general not uniquely determined, although this is the case for normalized barycentric coordinates with reference to a simplex. ${\displaystyle \mathbf {x} _{1},\dotsc ,\mathbf {x} _{n}}$ ${\displaystyle n}$ ${\displaystyle n-1}$

Generalized barycentric coordinates are used in particular in computer graphics and in geometric modeling . There, three-dimensional objects can often be approximated by polyhedra, so that the generalized barycentric coordinates have a geometric meaning and facilitate further processing of these objects.

Barycentric interpolation

An interpolation method that generalizes linear interpolation for functions of several variables is based on barycentric coordinates .

In the case of a function of two variables and are given for three points , and the function values. Here , and may not lie on a straight line. So you have to create a triangle . If an arbitrary point is now given, one defines ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle A(x_{A},y_{A})}$ ${\displaystyle B(x_{B},y_{B})}$ ${\displaystyle C(x_{C},y_{C})}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle ABC}$ ${\displaystyle (x,y)}$

${\displaystyle f(x,y)=a\,f(x_{A},y_{A})+b\,f(x_{B},y_{B})+c\,f(x_{C},y_{C})}$,

where are the normalized barycentric coordinates of . This interpolation also works for points outside the triangle. ${\displaystyle (a,b,c)}$ ${\displaystyle (x,y)}$

literature

• Oswin Aichholzer, Bert Jüttler: Introduction to applied geometry. Springer-Verlag, Basel 2013, doi : 10.1007 / 978-3-0346-0651-6 , ISBN 978-3-0346-0651-6 , p. 59.
• Gerald Farin, Diane Hansford: Linear Algebra: A Geometric Approach. Springer-Verlag, 2013, doi : 10.1007 / 978-3-642-55841-2 , ISBN 978-3-540-41854-2 , p. 139.
• John Fauvel, Raymond Flood, Robin Wilson: Möbius and his Band: The Rise of Mathematics and Astronomy in 19th Century Germany. Springer-Verlag, 2013, ISBN 978-3-0348-6203-5 , p. 106.
• Peter Knabner, Lutz Angermann: Numerics of partial differential equations. An application-oriented introduction. Springer 2000, ISBN 3-642-57181-6 , pp. 108-111 ( books.google.de ).
• Abraham A. Ungar: Barycentric Calculus in Euclidean and Hyperbolic Geometry. World Scientific 2010, ISBN 978-981-4304-93-1 .
• John Vince: Mathematics for Computer Graphics. Springer 2010, ISBN 978-1-84996-032-8 , pp. 208-236.

Web links

• Eric W. Weisstein : Barycentric Coordinates . In: MathWorld (English).
• Barycentric Coordinates. Entry in the Encyclopaedia of Mathematics .
• Barycentric Coordinates. Entry on PlanetMath .
• Philipp B. Laval: Mathematics for Computer Graphics - Barycentric Coordinates. (PDF; 137 kB).
• Barycentric coordinates with GeoGebra

Individual evidence

1. ↑ Max Koecher, Aloys Krieg: level geometry. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49328-0 , p. 76.
2. ↑ Josef Hoschek, Dieter Lasser: Fundamentals of geometrical data processing. Teubner-Verlag, 1989, ISBN 3-519-02962-6 , p. 243.
3. ↑ Gerald Farin: Curves and Surfeces for Computer Aided Geometric Design. Academic Press, 1990, ISBN 0-12-249051-7 , p. 20.
4. ^ Christian Gerthsen: Physics. Springer-Verlag, 1963, p. 37.
5. ↑ Felix Klein: Lectures on higher geometry. Springer-Verlag, 1926, p. 13.