Two-body problem in general relativity

The two-body problem of general relativity is a generalization of the two-body problem of classical mechanics and describes the problem of calculating the paths of two bodies that move relative to one another due to gravitational influences . The problem is examined within the framework of the general theory of relativity and was essential in Arthur Eddington's first experimental proof of the gravitational lensing effect ( solar eclipse 1919 ) .

For the sake of simplicity, the two bodies are assumed to be point-shaped so that, among other things, tidal forces can be neglected.

The general theory of relativity describes the gravitational field through curved spacetime. The field equations that determine this curvature are non-linear and therefore difficult to solve in closed form. An exact solution for the Kepler problem has not yet been found, but the Schwarzschild solution is a good approximation for many cases.

This solution describes the two-body problem well when the mass of one body is significantly greater than the mass of the other. In this case, the greater mass can be assumed to be stationary and the sole contribution to the gravitational field. This approximation describes, for example, the motion of a photon passing a star very well. The movement of the lighter body can then be determined from the Schwarzschild solution, resulting in a geodesic in a curved space-time. Such geodetic solutions explain the anomalous precession of the planet Mercury , which is an important piece of evidence for general relativity. They also describe the bending of light in a gravitational field, another prediction that is known to serve as evidence for general relativity. ${\displaystyle M}$ ${\displaystyle m}$

If it is assumed that both masses contribute to the gravitational field as in binary stars , the Kepler problem can only be approximately solved. The earliest approximation method to be developed was post-Newtonian expansion, an iterative method in which an initial solution is corrected gradually. Recently it has become possible to solve Einstein's field equation with a computer (numerical relativity). When the two bodies orbit each other, they emit gravitational radiation . This causes them to gradually lose energy and angular momentum, as shown by the binary pulsar PSR B1913 + 16 .

For binary black holes , a numerical solution to the two-body problem was found in 2005 after four decades of research.

Historical classification

For a long time Newton's discovery of gravity was considered complete. With his theory numerous celestial processes could be calculated and predicted very precisely. That this law might not be complete was only discovered in the late 19th century. The most recent and most accurate, well-confirmed theory of gravity to date is Einstein's general theory of relativity, which he published in 1915.

Kepler's laws

The figure shows the movement of a planet on an elliptical orbit around the sun in one of the focal points of the ellipse according to Kepler's first law

The first quantification of movements in the sky was achieved by the physicist Johannes Kepler in the early 17th century by formulating his three Kepler laws . Through numerous observations, Kepler succeeded in deriving three laws. These three laws are worded as follows:

1. Each planet's orbit around the sun is an ellipse with the sun at one of the two focal points.
2. A beam drawn from the sun to the planet covers areas of the same size at the same time.
3. The squares of the orbital times of two planets behave like the cubes of the major semiaxes of their orbital ellipses.

Kepler's laws are used to this day for simple problems in astronomy, as they give fairly accurate results for planetary masses that are small relative to the mass of the sun and small velocities compared to the speed of light. Kepler's laws are also considered to be one of the starting points for the classic two-body problem.

The classic two-body problem

The classic two-body problem:
With suitable starting conditions, two bodies move around each other on circular paths

When Kepler problem the orbits of the two bodies are ellipses with the same line of apsides , the same eccentricity and equal to their circulation time as fixed Considered barycenter (+)

→ Main article : Two-body problem

The British physicist Sir Isaak Newton first succeeded in quantifying gravity in 1684. He published his results for the first time in large numbers in his Philosophiae Naturalis Principia Mathematica in 1687. With this work, from today's perspective, he laid the foundation for the development of a consistent theory of gravity.

The two-body problem, which is based on Newton's law of gravitation, is particularly important in astronomy, since it can describe the orbits of two planets (or similar objects) with great accuracy . Its solution is a bit mathematically complex, which is why only the solution is outlined here.

By adding Newton's equations of motion of the two particles

${\displaystyle {\vec {F}}_{12}=m_{1}{\ddot {\vec {r}}}_{1}\quad {\text{und}}\quad {\vec {F}}_{21}=m_{2}{\ddot {\vec {r}}}_{2}}$

we get according to the interaction principle (actio = reactio)

${\displaystyle m_{1}{\ddot {\vec {r}}}_{1}+m_{2}{\ddot {\vec {r}}}_{2}={\vec {F}}_{12}+{\vec {F}}_{21}=0.}$

After the introduction of center of gravity coordinates, the result is with ${\displaystyle m_{1}{\ddot {\vec {r}}}_{1}+m_{2}{\ddot {\vec {r}}}_{2}=(m_{1}+m_{2}){\ddot {\vec {R}}}}$

${\displaystyle {\ddot {\vec {R}}}={\frac {m_{1}{\ddot {\vec {r}}}_{1}+m_{2}{\ddot {\vec {r}}}_{2}}{m_{1}+m_{2}}}=0}$

an inertial movement for the center of gravity of the two-body system: it moves in a straight line, its rest system is an inertial system. The movement of the individual mass points can be traced back to a one-body problem by transitioning to this so-called center of gravity system:

From the differential equation

${\displaystyle \mu \cdot {\ddot {\vec {r}}}(t)={\vec {F}}({\vec {r}}(t))}$

with the reduced mass we get the connection vector , which then results in total ${\displaystyle \mu :=(m_{1}\cdot m_{2})/(m_{1}+m_{2})}$ ${\displaystyle {\vec {r}}(t):={\vec {r}}_{1}-{\vec {r}}_{2}}$

${\displaystyle {\vec {r}}_{1}(t)={\vec {R}}(t)+{\frac {m_{2}}{m_{1}+m_{2}}}{\vec {r}}(t)}$

${\displaystyle {\vec {r}}_{2}(t)={\vec {R}}(t)-{\frac {m_{1}}{m_{1}+m_{2}}}{\vec {r}}(t)}$

for the movement of the two mass points.

Perihelion of Mercury

→ Main article : Perihelion of Mercury

The first doubts about Newton's law of gravitation arose with the discovery of the perihelion rotation of Mercury.

In 1859, Urbain Le Verrier discovered that the orbit of the planet Mercury was different from the orbit predicted by classical mechanics. The ellipse of its orbit rotated a little faster than expected, although all effects of the other planets had been taken into account. The effect is small (around 43 arcseconds per century), but is well above the measurement error (around 0.1 arcseconds per century).

Le Verrier quickly realized the importance of his discovery and began to look for reasons for this effect. In the course of this discussion, numerous assumptions were made: By taking into account interplanetary dust, an unobserved perishability of the sun or the existence of a new planet called Vulcan, this perihelion rotation could be explained using classical mechanics. However, these explanations could not satisfactorily explain the phenomenon, which is why more radical hypotheses were made. One hypothesis was that Newton's law of gravity was wrong. For example, some physicists suggested a power law with an exponent slightly different from 2. ${\displaystyle {\tfrac {1}{r^{2}}}}$

A clear and satisfactory answer was only given in the context of Einstein's general theory of relativity.

The general theory of relativity

Eddington's measurements during a solar eclipse in 1919 confirmed the effect of the curvature of light rays postulated by Einstein and thus led to worldwide acceptance of the theory

→ Main article : General theory of relativity

Numerous works from the period 1904–1905 - u. a. Works by Hendrik Lorentz , Henri Poincaré and finally Albert Einstein  - exclude movement at a speed greater than that of light. From this it follows that Newton's law of gravitation must be supplemented, which - according to Einstein's considerations - must be compatible with the principle of relativity and yet reproduce Newton's law of gravitation for negligible relativistic effects. Such attempts were made by Henri Poincaré (1905), Hermann Minkowski (1907) and Arnold Sommerfeld (1910).

In 1907 Einstein came to the conclusion that his special theory of relativity would have to be expanded. From 1907 to 1915, Einstein worked on a new theory, using his principle of equivalence as a key concept. The equivalence principle states that a uniform gravitational field acts equally on everything in it and therefore cannot be distinguished from a freely falling observer. Conversely, all local gravitational effects should be reproducible in a linearly accelerating reference system and vice versa.

Gravity acts like an apparent force (like centrifugal force or Coriolis force, which only occur in accelerated reference systems). All apparent forces are proportional to inertial mass, just like gravity. In order to bring about the unification of gravity and special relativity and to consider the equivalence principle, the classical assumption that our space obeys the laws of Euclidean geometry has to be given up.

Einstein used a more general geometry, pseudo-Riemannian differential geometry, to account for the necessary curvature of space and time. After eight years of work (1907–1915) he succeeded in establishing a connection between curvature and mass distribution that could explain gravitation. The first solutions to his field equations provided the unexplained precession of Mercury and predicted a bending of light in the presence of large masses. This gravitational lensing effect was confirmed after his theory was published. The solutions to these field equations and the mathematical principles are explained below.

Mathematical foundations of general relativity

In a flat room, the well-known Pythagorean theorem applies

${\displaystyle \mathrm {d} s^{2}=\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2},}$

where , and denote the infinitesimal changes between the , and coordinates of two points in a Cartesian coordinate system. In a curved space the metric is through ${\displaystyle \mathrm {d} x}$ ${\displaystyle \mathrm {d} y}$ ${\displaystyle \mathrm {d} z}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$

${\displaystyle \mathrm {d} s^{2}=F(x,y,z)\ \mathrm {d} x^{2}+G(x,y,z)\ \mathrm {d} y^{2}+H(x,y,z)\ \mathrm {d} z^{2}}$

given, where are arbitrary functions of the place. Such a curved metric represents the earth, for example. Such a metric can be passed through in spherical coordinates ${\displaystyle F,G,H}$ ${\displaystyle (r,\theta ,\varphi )}$

${\displaystyle \mathrm {d} s^{2}=\mathrm {d} r^{2}+r^{2}\mathrm {d} \theta ^{2}+r^{2}\sin ^{2}\theta \ \mathrm {d} \varphi ^{2}}$

describe. In the special theory of relativity (SRT) the metric in Cartesian coordinates is through

${\displaystyle c^{2}\mathrm {d} \tau ^{2}=c^{2}\mathrm {d} t^{2}-\mathrm {d} x^{2}-\mathrm {d} y^{2}-\mathrm {d} z^{2},}$

defined, whereby the invariant is called “proper time”. This metric can be noted in spherical coordinates as follows: ${\displaystyle \tau }$

${\displaystyle c^{2}\mathrm {d} \tau ^{2}=c^{2}\mathrm {d} t^{2}-\mathrm {d} r^{2}-r^{2}\mathrm {d} \theta ^{2}-r^{2}\sin ^{2}\theta \ \mathrm {d} \varphi ^{2}}$

In the general theory of relativity (GTR), however, both time and space are arbitrarily curved - which is why we have to formulate the distance between two points more generally:

${\displaystyle \mathrm {d} s^{2}=c^{2}\mathrm {d} \tau ^{2}=g_{\mu \nu }\mathrm {d} x^{\mu }\mathrm {d} x^{\nu }}$

Here the metric tensor denotes space-time. The metric tensor changes over to the Minkowski tensor in the SRT . ${\displaystyle g_{\mu \nu }}$ ${\displaystyle g_{\mu \nu }}$ ${\displaystyle \eta _{\mu \nu }=\operatorname {diag} (1,-1,-1,-1)}$

The equations of motion of the ART establish a connection between the curvature of a space and the mass distribution. From these field equations, equations of motion can be derived that we will need for our two-body problem.

The geodesic equation

→ Main article : Geodesic equation

According to the general theory of relativity, force-free particles move in space-time on geodesics , i.e. the shortest possible connections between two points. For non-curved spaces these are straight lines. The geodesic equation is:

${\displaystyle {\frac {\mathrm {d} ^{2}x^{\mu }}{\mathrm {d} q^{2}}}+\Gamma _{\nu \lambda }^{\mu }{\frac {\mathrm {d} x^{\nu }}{\mathrm {d} q}}{\frac {\mathrm {d} x^{\lambda }}{\mathrm {d} q}}=0}$

Here is a Christoffelsymbol of the second kind with ${\displaystyle \Gamma _{\nu \lambda }^{\mu }}$

${\displaystyle \Gamma _{\nu \lambda }^{\mu }={\frac {1}{2}}g^{\mu \kappa }(\partial _{\nu }g_{\lambda \kappa }+\partial _{\lambda }g_{\nu \kappa }+\partial _{\kappa }g_{\nu \lambda }).}$

In addition to the field equations, the geodesic equation is the most important equation for determining orbits, taking relativistic effects into account. The geodesic equation can be interpreted as an extremal problem: An object always moves on the shortest connection between two points. In flat space-time, objects move in straight lines, whereas in curved space-time they move generally. A. not.

The Schwarzschild solution

Comparison between the trajectory of a test particle in Newtonian spacetime and Schwarzschild spacetime in a strong gravitational field (r0 = 10 rs = 20GM / c²). The initial speed for both objects is 126% of the circular path speed, φ0 is the starting angle. Since the metric is rotationally symmetrical, the reference system can be rotated so that φ is constant and the movement takes place in the r-θ-plane (or vice versa).

→ Main article : Schwarzschild metric

The Schwarzschild matrix is ​​an exact solution of Einstein's field equations. This metric is based on the gravitational field of a stationary, uncharged and non-rotating body of mass . This solution is characterized by the length , the so-called Schwarzschild radius: ${\displaystyle M}$ ${\displaystyle r_{\mathrm {s} }}$

${\displaystyle r_{\mathrm {s} }={\frac {2GM}{c^{2}}}}$

The Schwarzschild metric thus represents a special case of the two-body problem, in which the mass is at rest and a second body of the mass moves around it. ${\displaystyle M}$ ${\displaystyle m}$

The line element of the Schwarzschild solution in natural units is

${\displaystyle \mathrm {d} s^{2}=g_{\mu \nu }\mathrm {d} x^{\mu }\mathrm {d} x^{\nu }=-c^{2}\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\ \mathrm {d} t^{2}+{\frac {1}{1-{\frac {r_{\mathrm {s} }}{r}}}}\mathrm {d} r^{2}+r^{2}\mathrm {d} \theta ^{2}+r^{2}\sin ^{2}(\theta )\ \mathrm {d} \phi ^{2},}$

from which the metric tensor to

${\displaystyle g_{\mu \nu }=\operatorname {diag} \left(-c^{2}\left(1-{\frac {r_{\mathrm {s} }}{r}}\right),{\frac {1}{1-{\frac {r_{\mathrm {s} }}{r}}}},r^{2},r^{2}\sin ^{2}\theta \right)}$

can be read.

Orbits around a central mass

The orbits of a test mass around an infinitely large central mass can be determined by the equation of motion ${\displaystyle m}$

${\displaystyle \left({\frac {\mathrm {d} r}{\mathrm {d} \tau }}\right)^{2}={\frac {E^{2}}{m^{2}c^{2}}}-\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\left(c^{2}+{\frac {h^{2}}{r^{2}}}\right)}$

where the reduced mass denotes the specific relative angular momentum. Reshaping according to the orbit provides the equation ${\displaystyle h:=r\times v=L/\mu }$ ${\displaystyle \mu \approx m}$

${\displaystyle \left({\frac {\mathrm {d} r}{\mathrm {d} \varphi }}\right)^{2}={\frac {r^{4}}{b^{2}}}-\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\left({\frac {r^{4}}{a^{2}}}+r^{2}\right)}$.

To simplify matters, the abbreviations and were introduced in this step . Both variables are conserved and depend on the initial values ​​of the location and the velocity of the test particle. Therefore the general solution of the equation of motion can be noted as follows: ${\displaystyle a:=h/c}$ ${\displaystyle b:=Lc/E}$

${\displaystyle \varphi =\int {\frac {1}{r^{2}}}\left[{\frac {1}{b^{2}}}-\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)\left({\frac {1}{a^{2}}}+{\frac {1}{r^{2}}}\right)\right]^{-{\frac {1}{2}}}\mathrm {d} r}$

Effective potential of the Schwarzschild metric

The above equation of motion

${\displaystyle \left({\frac {\mathrm {d} r}{\mathrm {d} \tau }}\right)^{2}={\frac {E^{2}}{m^{2}c^{2}}}-c^{2}+{\frac {r_{\mathrm {s} }c^{2}}{r}}-{\frac {h^{2}}{r^{2}}}+{\frac {r_{\mathrm {s} }h^{2}}{r^{3}}}}$

can be noted with the Schwarzschild radius as follows: ${\displaystyle r_{\mathrm {s} }}$

${\displaystyle {\frac {1}{2}}m\left({\frac {\mathrm {d} r}{\mathrm {d} \tau }}\right)^{2}=\left({\frac {E^{2}}{2mc^{2}}}-{\frac {1}{2}}mc^{2}\right)+{\frac {GMm}{r}}-{\frac {L^{2}}{2\mu r^{2}}}+{\frac {G(M+m)L^{2}}{c^{2}\mu r^{3}}}}$

This equation is equivalent to the motion of a test particle in a one-dimensional effective potential:

${\displaystyle V(r)=-{\frac {GMm}{r}}+{\frac {L^{2}}{2\mu r^{2}}}-{\frac {G(M+m)L^{2}}{c^{2}\mu r^{3}}}}$

The first two terms are known from classical mechanics: The first term is the potential energy of the Newtonian gravitational field and the second term is equivalent to the potential energy of the rotation. The third term only occurs in general relativity. This term ensures that an elliptical orbit moves gradually through one angle per revolution: ${\displaystyle \delta \phi }$

${\displaystyle \delta \phi \approx {\frac {6\pi G(M+m)}{c^{2}A\left(1-e^{2}\right)}}}$

Here, the major semi-axis and the eccentricity. Attention: does not stand for the change in the coordinate of the space-time coordinates , but for the change in the argument of the periapsis of the classical Kepler orbit. ${\displaystyle A}$ ${\displaystyle e}$ ${\displaystyle \delta \phi }$ ${\displaystyle \varphi }$ ${\displaystyle (t,r,\theta ,\varphi )}$ ${\displaystyle \phi }$

The third energy term is attractive and dominates at small radii, which results in a critical inner radius from which a test particle is inexorably drawn into the interior, up to coordinate singularity . This inner radius is a function of the angular momentum of the particle per unit of mass. ${\displaystyle r=0}$

Circular orbits and their stability

The figure shows the effective radial potential for different angular momenta. At small radii the energy drops steeply, which means that the particle is inexorably drawn inwards . However, if the normalized angular momentum is the same , a metastable circular path is possible. This radius is marked in green. At higher angular momentum there is a significant centrifugal barrier (light green curve) and an unstable inner radius, which is highlighted in red. ${\displaystyle r=0}$ ${\displaystyle a/r_{\mathrm {s} }=L/(mcr_{\mathrm {s} })}$ ${\displaystyle {\sqrt {3}}}$

The stable and unstable radii are plotted against the angular momentum in blue and red. These curves meet on a unique circular path (green circle) if the normalized angular momentum is the same . For comparison, the classic radius, which is predicted from the centripetal acceleration and Newton's law of gravity, is shown in black. ${\displaystyle a/r_{\mathrm {s} }=L/(mcr_{\mathrm {s} })}$ ${\displaystyle {\sqrt {3}}}$

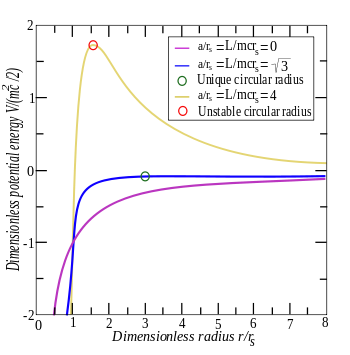
With the length , the effective potential of the Schwarzschild metric can be written as follows: ${\displaystyle a={\tfrac {h}{c}}}$

${\displaystyle V(r)={\frac {mc^{2}}{2}}\left(-{\frac {r_{\mathrm {s} }}{r}}+{\frac {a^{2}}{r^{2}}}-{\frac {r_{\mathrm {s} }a^{2}}{r^{3}}}\right)}$

Circular paths are possible exactly when the effective force disappears. The force is known to be the negative derivative of the potential:

${\displaystyle F=-{\frac {\mathrm {d} V}{\mathrm {d} r}}=-{\frac {mc^{2}}{2r^{4}}}\left(r_{\mathrm {s} }r^{2}-2a^{2}r+3r_{\mathrm {s} }a^{2}\right)=0}$

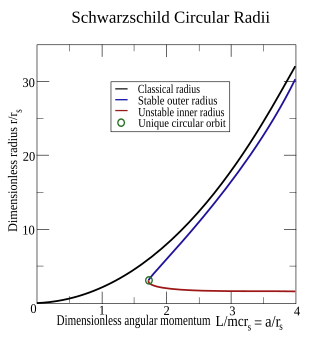
There are two radii for which this equation applies. We call these two radii and : ${\displaystyle r_{\text{innen}}}$ ${\displaystyle r_{\text{außen}}}$

${\displaystyle {\begin{aligned}r_{\text{außen}}&={\frac {a^{2}}{r_{\mathrm {s} }}}\left(1+{\sqrt {1-{\frac {3r_{\mathrm {s} }^{2}}{a^{2}}}}}\right)\\r_{\text{innen}}&={\frac {a^{2}}{r_{\mathrm {s} }}}\left(1-{\sqrt {1-{\frac {3r_{\mathrm {s} }^{2}}{a^{2}}}}}\right)={\frac {3a^{2}}{r_{\text{außen}}}},\end{aligned}}}$

which result from the addition of the square of the force equation. The inner radius describes an unstable path, since the third attractive force becomes stronger faster than the other two forces when it becomes smaller. Because if the particle slightly deviates from its orbit, it will be pulled by the third force . The outer radius , on the other hand, describes stable orbits, since the third force term only dominates for small radii, and the system behaves similarly to the non-relativistic two-body problem. ${\displaystyle r}$ ${\displaystyle r\to 0}$ ${\displaystyle r_{\text{außen}}}$

If is, then the two radii merge into the classical formulas: ${\displaystyle a\gg r_{\mathrm {s} }}$

${\displaystyle {\begin{aligned}r_{\text{außen}}&\approx {\frac {2a^{2}}{r_{\mathrm {s} }}}\\r_{\text{innen}}&\approx {\frac {3}{2}}r_{\mathrm {s} }\end{aligned}}}$

Putting the definitions of and in provides the classic formula for a crowd encircling a body of the crowd . the equation ${\displaystyle a}$ ${\displaystyle r_{\mathrm {s} }}$ ${\displaystyle r_{\text{außen}}}$ ${\displaystyle m}$ ${\displaystyle M}$

${\displaystyle r_{\text{außen}}^{3}={\frac {G(M+m)}{\omega _{\varphi }^{2}}}}$

with the angular velocity results in Newtonian mechanics by equating the centrifugal force with the gravitational force: ${\displaystyle \omega _{\varphi }}$

${\displaystyle {\frac {GMm}{r^{2}}}=\mu \omega _{\varphi }^{2}r}$

Where is the reduced mass . The following applies to the classic angular velocity: ${\displaystyle \mu }$

${\displaystyle \omega _{\varphi }^{2}\approx {\frac {GM}{r_{\text{außen}}^{3}}}={\frac {r_{\mathrm {s} }c^{2}}{2r_{\text{außen}}^{3}}}={\frac {r_{\mathrm {s} }c^{2}}{2}}\cdot {\frac {r_{\mathrm {s} }^{3}}{8a^{6}}}={\frac {c^{2}r_{\mathrm {s} }^{4}}{16a^{6}}}}$

If, however, and are the same, the two radii merge into one another: ${\displaystyle a^{2}}$ ${\displaystyle r^{3}}$

${\displaystyle r_{\text{außen}}\approx r_{\text{innen}}\approx 3r_{\mathrm {s} }}$

For massless particles (e.g. photons) , what a path implies at applies . This path is known in English as the photon sphere , as the path from which photons are forced onto circular paths by gravity. ${\displaystyle a\to \infty }$ ${\displaystyle r_{\text{innen}}={\frac {3}{2}}r_{\mathrm {s} }}$

Precession of elliptical orbits

In the classic two-body problem, a particle always follows the same perfect ellipse (red). According to the general theory of relativity, there is a third attractive force by which the particle is attracted a little more strongly than by Newton's gravitational force, especially with large radii. This force causes the particle to precession in the direction of its rotation. The yellow point is the center of attraction (e.g. the sun).

The precession of the orbit can be derived from the effective radial potential. A small radial deviation from a circular path of the radius oscillates stably with the angular velocity ${\displaystyle r_{\text{außen}}}$

${\displaystyle \omega _{r}^{2}={\frac {1}{m}}\left[{\frac {\mathrm {d} ^{2}V}{\mathrm {d} r^{2}}}\right]_{r=r_{\text{außen}}}}$

${\displaystyle \omega _{r}^{2}={\frac {c^{2}r_{\mathrm {s} }}{2r_{\text{außen}}^{4}}}\cdot \left(r_{\text{außen}}-r_{\text{innen}}\right)=\omega _{\varphi }^{2}{\sqrt {1-{\frac {3r_{\mathrm {s} }^{2}}{a^{2}}}}}.}$

Square root on both sides and expansion through the binomial theorem gives

${\displaystyle \omega _{r}=\omega _{\varphi }\left(1-{\frac {3r_{\mathrm {s} }^{2}}{4a^{2}}}+\dotsb \right).}$

Multiplication with the orbital time of one revolution gives the precession of the orbit per revolution ${\displaystyle T}$

${\displaystyle \delta \varphi =T\left(\omega _{\varphi }-\omega _{r}\right)\approx 2\pi \cdot {\frac {3r_{\mathrm {s} }^{2}}{4a^{2}}}={\frac {3\pi m^{2}c^{2}}{2L^{2}}}r_{\mathrm {s} }^{2},}$

where we and have made use of the definition of the length scale . ${\displaystyle \omega _{\phi }T=2\pi }$ ${\displaystyle a}$

Inserting the definition of the Schwarzschild radius yields ${\displaystyle r_{\mathrm {s} }={\frac {2GM}{c^{2}}}}$

${\displaystyle \delta \varphi \approx {\frac {3\pi m^{2}c^{2}}{2L^{2}}}\cdot {\frac {4G^{2}M^{2}}{c^{4}}}={\frac {6\pi G^{2}M^{2}m^{2}}{c^{2}L^{2}}}.}$

The term can be given by introducing the semi-major axis and the eccentricity passing through ${\displaystyle A}$ ${\displaystyle e}$

${\displaystyle {\frac {h^{2}}{G(M+m)}}=A\left(1-e^{2}\right)}$

related to the precession angle

${\displaystyle \delta \varphi \approx {\frac {6\pi G(M+m)}{c^{2}A\left(1-e^{2}\right)}}}$

to lead. Since the closed classical orbit is generally an ellipse, the size is the semi-latus rectum (the half parameter) of the ellipse. ${\displaystyle A(1-e^{2})}$

Therefore, the final formula of the apsidal angle precession for one complete revolution is:

${\displaystyle \delta \varphi \approx {\frac {6\pi G(M+m)}{c^{2}l}}}$

Post-Newtonian extensions

Overview of different parameters with different approximations

Post-Newtonian approximation

For the Schwarzschild solution of Einstein's field equations, the assumption is necessary that the larger mass is stationary and characterizes the strength of the gravitational field alone (e.g. the space-time curvature). Because then the movement of the smaller mass can be calculated with the help of the geodesic equation. For photons and the orbit of the planet Mercury around the sun, this is a reasonable assumption, since Mercury is about six million times lighter than the sun. This assumption does not make sense for other astronomical processes such as orbiting two black holes. ${\displaystyle M}$ ${\displaystyle m}$

There are no closed solutions for this case, which is why we rely on numerical methods to solve the field equations. One of these approximations is the Post-Newtonian approximation. This numerical method is based on given initial solutions for the motion of a particle and is used for the calculation of gravitational fields. With this calculated gravitational field, particle movements can be calculated again, from which more precise fields can be determined. We call this approach Post-Newtonian approximation, since Newton's solutions for the orbit of the particles are often used as the starting solution.

The experimentally observed decrease in the orbit time of the binary pulsar PSR B1913 + 16 (blue measuring points) agree almost perfectly with the predictions of the general theory of relativity (black curve)

If we apply this method to the two-body problem without restricting the masses of the bodies, the result is quite simple. As a first approximation we get that the motion of the two particles is equivalent to the motion of an infinitesimal particle in the gravitational field of the common mass. In this case we can continue to use the Schwarzschild solution by replacing the field-generating mass with the total mass . ${\displaystyle M}$ ${\displaystyle M+m}$

Computer simulations

Einstein's field equations can now be solved using complex numerical methods. With enough computing power, these solutions are more accurate than those found with traditional solutions. These simulations are very computationally heavy and require enormous computing resources.

Despite these problems, by the late 1990s it was possible to simulate complicated problems with computer help. For example, the merging of two black holes was observed on a computer for the first time and was only proven experimentally much later through the discovery of gravitational waves.

The merging of two black holes has long been considered one of the most complicated cases of the two-body problem in general relativity. This possibility of simulation shortened the process of identifying the cause of the gravitational wave signal measured at the LIGO as a merging of two black holes. Because this scenario had already been simulated, the researchers quickly recognized the typical values ​​of this merger and were thus able to determine the masses and the location of the black holes in good approximation.

Gravitational radiation

The illustration shows two neutron stars rotating very quickly around each other and emitting energy in the form of gravitational waves. Due to the loss of energy, the two stars orbit each other faster and get closer and closer

Two bodies orbiting each other emit gravitational radiation, which gradually causes the orbits of the objects to lose energy.

Two neutron stars rotating rapidly around each other gradually lose energy by emitting gravitational radiation. When they lose energy, they circle around each other faster and closer.

The formulas describing the loss of energy and angular momentum due to the gravitational radiation of the two bodies of the Kepler problem have already been determined. The speed of energy loss (averaged over a complete orbit) is given by

${\displaystyle -\left\langle {\frac {\mathrm {d} E}{\mathrm {d} t}}\right\rangle ={\frac {32G^{4}m_{1}^{2}m_{2}^{2}\left(m_{1}+m_{2}\right)}{5c^{5}a^{5}\left(1-e^{2}\right)^{\frac {7}{2}}}}\left(1+{\frac {73}{24}}e^{2}+{\frac {37}{96}}e^{4}\right)}$.

The angle brackets on the left indicate that an entire orbit is being averaged. Similar to this formula results in the average loss of angular momentum

${\displaystyle -\left\langle {\frac {\mathrm {d} L_{z}}{\mathrm {d} t}}\right\rangle ={\frac {32G^{\frac {7}{2}}m_{1}^{2}m_{2}^{2}{\sqrt {m_{1}+m_{2}}}}{5c^{5}a^{\frac {7}{2}}\left(1-e^{2}\right)^{2}}}\left(1+{\frac {7}{8}}e^{2}\right).}$

The reduction in orbit time is described by

${\displaystyle -\left\langle {\frac {\mathrm {d} P_{b}}{\mathrm {d} t}}\right\rangle ={\frac {192\pi G^{\frac {5}{3}}m_{1}m_{2}\left(m_{1}+m_{2}\right)^{-{\frac {1}{3}}}}{5c^{5}\left(1-e^{2}\right)^{\frac {7}{2}}}}\left(1+{\frac {73}{24}}e^{2}+{\frac {37}{96}}e^{4}\right)\left({\frac {P_{b}}{2\pi }}\right)^{-{\frac {5}{3}}},}$

where is the classic period of revolution. ${\displaystyle P_{b}}$

The loss of energy and angular momentum increases significantly when the eccentricity of the orbits approaches the number 1. The radiation power also increases significantly when the major semi-axis of the orbit decreases. ${\displaystyle a}$

Individual evidence

1. ^ ^{A b} Frans Pretorius: Evolution of Binary Black Hole Spacetimes . In: Physical Review Letters . September 14, 2005, ISSN  0031-9007 , doi : 10.1103 / PhysRevLett.95.121101 , PMID 16197061 , arxiv : gr-qc / 0507014 , bibcode : 2005PhRvL..95l1101P .
2. ^ ^{A b c} M. Campanelli, CO Lousto, P. Marronetti, Y. Zlochower: Accurate Evolutions of Orbiting Black-Hole Binaries without Excision . In: Physical Review Letters . March 22, 2006, ISSN  0031-9007 , doi : 10.1103 / PhysRevLett.96.111101 , PMID 16605808 , arxiv : gr-qc / 0511048 , bibcode : 2006PhRvL..96k1101C .
3. ^ ^{A b c} John G. Baker, Joan Centrella, Dae-Il Choi, Michael Koppitz, James van Meter: Gravitational-Wave Extraction from an Inspiraling Configuration of Merging Black Holes . In: Physical Review Letters . March 22, 2006, ISSN  0031-9007 , p. 435-440 , doi : 10.1103 / PhysRevLett.96.111102 , PMID 16605809 , bibcode : 2006PhRvL..96k1102B .
4. ^ Paulin Paris: Nouvelles recherches sur la vie de Froissart et sur les différentes date de ses chroniques . In: Comptes-rendus des séances de l année - Académie des inscriptions et belles-lettres . tape 3 , no. 1 , 1859, ISSN  0065-0536 , p. 227-229 , doi : 10.3406 / crai.1859.66255 .
5. ^ Weinberg, 1972.
6. ^ PC Peters, J. Mathews: Gravitational Radiation from Point Masses in a Keplerian Orbit . In: Physical Review . tape 131 , no. 1 , July 1, 1963, ISSN  0031-899X , p. 435-440 , doi : 10.1103 / PhysRev.131.435 .
7. ↑ ^{a b} L. D. Landau, EM Lifshitz: Electromagnetic waves . In: The Classical Theory of Fields . Elsevier, 1975, ISBN 978-0-08-025072-4 , pp. 109-129 , doi : 10.1016 / b978-0-08-025072-4.50013-7 .