Equivalence principle (physics)

The equivalence principle of physics expresses that the heavy and the inertial mass of a body are two equivalent quantities. This formulation reflects the early statements of Galileo Galilei and Isaac Newton in modern expression that all bodies are accelerated equally during free fall or that all gravitational effects are proportional to the mass of the bodies involved. From 1907 onwards, Albert Einstein recognized a possible basic principle of a theory of gravitation , which finally led him to the general theory of relativity .
The equivalence principle exists in two forms: According to the weak equivalence principle , of all properties of a body alone its mass (i.e. the measure of its inertia ) determines which gravity acts on it in a given homogeneous gravitational field . Its other properties such as chemical composition, size, shape etc. have no influence. According to the strong principle of equivalence , gravitational and inertial forces are equivalent on small distance and time scales in the sense that they cannot be distinguished by their effects either with mechanical or any other observations. The weak follows from the strong equivalence principle; Whether this also applies the other way round may depend on the exact formulation and has not yet been conclusively clarified.
The weak equivalence principle is a consequence of Newton's law of gravitation in classical mechanics. As a result, all bodies in free fall in an external gravitational field (with the same initial conditions) describe the same orbit in the same time. Therefore, relative to a moving frame of reference, there is no effect of the external gravitational field on the movement of the body during free fall, which is called the state of weightlessness .
Equivalence of inert and heavy mass
As inertial mass is the mass in Newton's second law refers to:
The Newton's first axiom expresses that bodies are lazy: they remain in their state of motion unless a force acts on it. The second axiom quantifies inertia: the more inertial mass a body has, the greater the force must be to give it a certain acceleration. The inert mass is additive: If you put together a body from components, then their inert masses add up, if you can neglect the binding energies of the components.
The heavy mass is a measure of the gravitational attraction of two bodies. In classical mechanics , the gravitational force is described by Newton's law of gravitation . A heavy mass body pulls another heavy mass body at a distance with a force of amount
on. Just like the inert mass, the heavy mass is additive: If you put together a body from components, then its heavy masses add up if you can neglect the binding energies.
Both types of mass are a priori independent of one another, such as B. the inertial mass of a particle and its electrical charge . But all experiments carried out so far confirm that the heavy mass of a body corresponds to its inert mass. Inertial and heavy mass are equivalent. This experimental result is called the weak equivalence principle .
The weak equivalence principle manifests itself in Galileo's law of fall , that all bodies fall at the same speed. In the earth's gravitational field the following applies approximately to a body of heavy mass
as the law of gravity, with the acceleration due to gravity . If one neglects frictional forces and buoyancy, the acceleration of the body results from the second axiom to
The equivalence principle now lists
All bodies fall in the same way (in a vacuum) in the earth's gravitational field, regardless of their mass. If the weak equivalence principle were violated, this law would also be invalid. This can be verified experimentally.
Since the law of inertia and Newton's law of gravity are based on independent physical findings and axioms, the weak equivalence principle remains unexplained in classical mechanics.
Experimental review
Isaac Newton (shown in his Principia , first edition 1687) and Friedrich Wilhelm Bessel (1832) in the form of pendulum tests made the first attempts at inert and heavy mass . Further investigations were carried out in 1890 and 1909 by the Hungarian physicist Loránd Eötvös in the Eötvös experiment named after him , which was repeated in an improved form in 1964 by Roll, Krotkov and Dicke in Princeton and in 1972 by Braginsky and Panov in Moscow. Quantitatively, such measurements become the equivalence of inert and heavy mass through the so-called Eötvös ratio
described, wherein and represent the measured accelerations of two different test bodies. While the classic pendulum tests by Newton and Bessel reached an upper limit of , the torsion pendulum tests by Eötvös (1909) improved this limit . In 1976 , Irwin Shapiro was able to prove the validity of the equivalence principle with an accuracy of 10 −12 through experiments with the laser reflectors that had been set up on the moon during Apollo missions ( Lunar Laser Ranging ) . Eric G. Adelberger et al. a. from the Eötvös group published a paper in 1999 that confirmed this principle with an accuracy of 10 −13 .
Stricter upper limits can be set through satellite-based experiments such as B. achieve the STEP mission (Satellite Test of the Equivalence Principle), Gravity Probe A or Microscope . Here z. B. the relative accelerations of in orbit, free-falling test bodies with different chemical compositions are measured, which should lead to an expected accuracy of (Microscope) and (STEP). Here, more directly than in previous experiments, the formulation of the equivalence principle of general relativity (GTR) is checked.
Principle of equivalence in general relativity
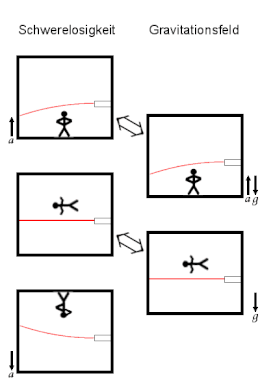
Acceleration of space Gravitational acceleration Equivalence principle: In free fall (bottom right) the physical phenomena are the same as in weightlessness (middle left). In a system in which and are opposite and of equal size, both the observer and the light beam behave as if the room were being accelerated upwards. So gravity has no influence on the physics in space. Note: The curvature of the laser beam is heavily exaggerated.
The consequence of the weak equivalence principle is that an observer in a closed laboratory, without information from outside, cannot read from the mechanical behavior of objects in the laboratory whether he is in weightlessness or in free fall (see figure opposite). This is equivalent to saying that gravitational forces are equivalent to inertial forces. Therefore, gravitational forces can be locally eliminated by changing to an accelerated reference system.
This principle was generalized by Einstein in 1907:
- Einstein's strong equivalence principle states that an observer in a closed laboratory without interaction with the environment cannot determine by any experiment whether he is in weightlessness far away from masses or in free fall close to a mass.
An equivalent but mathematized formulation of the strong equivalence principle, expressed in terms of general relativity , reads:
- A homogeneous gravitational field corresponds to a uniform acceleration in a flat space-time. In addition, in the coordinate system of a freely falling observer, the metric for small spatiotemporal distances from the reference spatiotemporal point deviates only slightly from a flat metric .
This can be represented quantitatively by means of Fermian normal coordinates, which show that the deviations from the flat metric are proportional to the curvature tensor .
- In short: In the local inertial system the laws of the SRT apply .
However, it must be noted that this principle only applies locally:
- An object located “below” (closer to the center of gravity) is attracted more strongly than an object located further “above”. If the free falling space is large enough in the vertical direction, the observer will therefore notice that objects that are further up are moving away from those that are further down.
- Conversely, with sufficient horizontal expansion of the space, the direction of the force of attraction on two objects that are horizontally distant from each other will differ noticeably, since they are both accelerated in the direction of the center of gravity. Therefore, the free-falling observer will notice that bodies that are far apart are moving towards each other. An expanded body will experience a force that pulls it apart in one direction and compresses it in the perpendicular directions.
Since the electric field of charged bodies also has a large expansion, there is a controversy about whether the principle of equivalence applies to such particles.
The weak equivalence principle cannot be explained by classical mechanics. On the other hand, in the GTR, the strong equivalence principle is raised to the starting point of the theory: Test particles, regardless of their composition or other nature, run through the same fall curve if their location and speed initially match. In the Newtonian sense, inert and passive heavy masses, between which one cannot differentiate in the GTR, are equivalent. The fact that all test particles run through the same fall curves results in the ART from the fact that the Lagrangian of the ART does not change when the coordinates are changed. The equivalence principle is thus present as a fundamental symmetry in the theory.
The observation of a violation of the equivalence principle would therefore show that the GTR would only be valid to a limited extent. With today's measurement accuracy, no deviations from the equivalence principle have been observed.
In addition, an active equivalence principle applies in the GTR, namely that different matter or radiation generate the same gravitation if only their energy-momentum tensor coincides.
literature
- Claus Lämmerzahl, Hansjörg Dittus: The equivalence principle on the test bench. In: Physics in Our Time. 1999, issue 2.
Web links
- Clifford M. Will: Page no longer available , search in web archives: The confrontation between general relativity and experiment, Living Reviews Relativity. Section 2.1. The Einstein Equivalence Principle.
- Markus Pössel: Cabin, gravity and rocket: the principle of equivalence. In: Einstein Online. Volume 4 (2010), 1111.
Individual evidence
- ↑ FW Bessel: Experiments on the force with which the earth attracts bodies of different properties. Berlin 1832.
- ↑ PG Roll, R. Krotkov, RH Dicke: The equivalence of inertial and passive gravitational mass. In: Annals of Physics. 26 (1964), 442-517, doi: 10.1016 / 0003-4916 (64) 90259-3 .
- ↑ Irwin I. Shapiro, Charles C. Counselman, III, Robert W. King: Verification of the Principle of Equivalence for Massive Bodies. In: Phys. Rev. Lett. 36 : 555-558 (1976), doi: 10.1103 / PhysRevLett.36.555 .
- ^ Rutherford Appleton Lab .: STEP: Satellite Test of the Equivalence Principle. ( Memento of July 16, 2011 in the Internet Archive ). Quote: "STEP aims to measure equivalence at the level of 1 part in 10 18. " Retrieved June 28, 2007.
- ↑ Albert Einstein: About the principle of relativity and the conclusions drawn from it. Archived from the original on March 9, 2017. In: Yearbook of radioactivity . 4, pp. 411-462.
-
↑ The word equivalence principle appears first in:
Einstein: Speed of light and statics of the gravitational field. In: Annals of Physics. Vol. 38, 1912, p. 355, online. ( Memento of March 7, 2016 in the Internet Archive ).
But he already explains it in detail in:
Einstein: On the influence of gravity on the spread of light. In: Annals of Physics. Vol. 35, 1911, p. 898. - ↑ T. Fließbach: General Theory of Relativity. Spectrum (2006), ISBN 978-3-8274-1685-8 , p. 51.
- ^ AK Singal: The Equivalence Principle and an Electric Charge in a Gravitational Field II. A Uniformly Accelerated Charge Does Not Radiate. In: General Relativity and Gravitation. 27: 1371-1390 (1997).
- ↑ Stephen Parrot: Radiation from a Uniformly Accelerated Charge and the Equivalence Principle. In: Found. Phys. 32: 407-440 (2002).
- ↑ Øyvind Grøn, Sigurd Kirkevold Næss: An electromagnetic perpetuum mobile? 2008.
- ↑ Norbert Dragon: Geometry of the theory of relativity. ( Memento from April 19, 2009 in the Internet Archive ). (PDF; 2.5 MB).





















