Track element
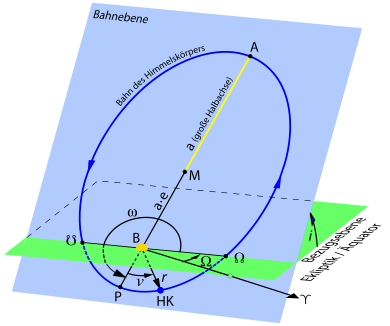
Six orbit elements
a : Length of the major semi-axis
e : Numerical eccentricity
i : Orbital inclination, inclination
Ω: Length / right ascension of the ascending node
ω : Argument of the periapsis, periapsis distance
t : Time of the Periapsis passage, periapsis time, epoch of the periapsis passage
Further designations
M: Ellipse center. B: focus, central body, sun / earth. P: periapsis. A: Apoapsis. AP: apse line. HK: Celestial body, planet / satellite. ☋: descending node. ☊: ascending node. ☋☊: knot line. ♈: spring equinox. ν : true anomaly. r : distance of the celestial body HK from the central body B
Orbit elements describe the path and movement of an astronomical object that obeys Kepler's laws in the gravitational field of a celestial body ( two-body problem ).
If no path disturbances are to be taken into account, six path elements are sufficient for a complete description. Two orbit elements describe the shape of the orbit, three elements describe the position of the orbit in space and one element is the point in time at which the celestial body passes a certain point on the orbit. The most common path described with elements is the ellipse.
In addition to the 6 elements of an undisturbed movement on a Kepler ellipse, satellite orbit elements usually contain other parameters with which orbital disturbances are taken into account.
The orbit elements in an elliptical orbit
Central body-specific information is, as in the figure above, marked by a slash in the sequence sun / earth.
Design elements
The description of the shape of the trajectory requires two values that determine the shape and size:
- The numerical eccentricity .
- The semi-major axis .
The following can be derived from this:
- The half parameter . With it, resulting parametric representation of the Keplerian orbit : .
- The periapsis distance: distance from the main vertex to the focal point .
- The angle of eccentricity
Location elements
The position in space relative to a reference system is determined by three parameters:
- the inclination : This is the angle of the path plane to the reference plane .
- the angle of the ascending node (length / right ascension of the node) : The angle from the reference plane reference direction to the ascending node (at the intersection of the reference plane and the path plane).
- the argument of the periapsis : the angle from the ascending node to the periapsis (point of the orbit closest to the center on the major semi-axis).
Time reference
The time reference defines the time zero point:
- Epoch of the passage of the periapsis of the body.
Derived quantities
- Mean movement : mean angular velocity of the mean anomaly
The orbital time as the seventh orbital element
Strictly speaking, the orbital time as the seventh orbital element belongs to the independent quantities necessary for the general description of the two-body problem. It is often not specified because it and the major semi-axis are linked to one another via the law of gravitation, and the mass of the body under consideration is negligible compared to that of the central body. If the mass of the smaller body also has to be considered in the law of gravitation, it is indirectly the seventh orbital element.
The specification of path elements
The 6-tuple is called a classic orbit element .
There are also other options that are adapted to the respective case:
- is particularly suitable for comets and the planets of the solar system.
- for Pluto and the minor planets as used in the Astronomical Almanac .
- gives the planetary theory VSOP 82 in an indirect way.
- the system of NASA / NORAD Two Line Elements Format for artificial earth satellites
Overview
| Track element | Usability | ||||
|---|---|---|---|---|---|
| Track element | reference | symbol | dimension | ellipse | Parabola / hyperbola |
| Numerical eccentricity | shape | e , ε | 1 | Yes | Yes |
| Eccentricity angle | shape | Φ | 1 | Yes | No |
| Semi-parameters | size | p | length | Yes | Yes |
| Periapsis distance | size | r min | length | Yes | Yes |
| Major semi-axis | size | a , α | length | Yes | No |
| Inclination, orbit inclination | location | i | angle | Yes | Yes |
| Angle of the knot | location | Ω | angle | Yes | partly 1 |
| Argument of the periapsis | location | ω | angle | Yes | Yes |
| Medium movement | Timing | μ , n , V | 1 / time | Yes | Yes |
| Angular velocity 2 | Time-place behavior | Angle / time | Yes | Yes | |
| Mean anomaly 2 | Railway location | M. | angle | Yes | No |
| Medium length 2 | Railway location | λ , L | angle | Yes | No |
| Radius vector 2 | Railway location | length | Yes | Yes | |
| Period of circulation | Time reference | P | time | Yes | No |
| Periapsis period | Time reference | t | time | Yes | Yes |
See also
literature
- Andreas Guthmann: Introduction to celestial mechanics and ephemeris calculus. BI-Wiss.-Verl., Mannheim 1994, ISBN 3-411-17051-4
- Wolfgang Vollmann: Changing star locations . In: Hermann Mucke (Hrsg.): Modern astronomical phenomenology. 20th Sternfreunde Seminar, 1992/93. Zeiss Planetarium of the City of Vienna and Austrian Astronomical Association 1992, pp. 55–102 ( weblink, Feb. 3, 2011 )
- Jean Meeus: Astronomical Algorithms . Willmann-Bell, Richmond 1991, ISBN 0-943396-35-2
Web links
- Minor Planet Center (English)
- Central Bureau for Astronomical Telegrams (English)
Individual evidence
- ↑ Oliver Montenbruck: Fundamentals of the Ephemeris Calculation , Stars and Space, Heidelberg 2001, ISBN 3-87973-941-2 , p. 57
- ↑ Guthmann , p. 163
- ↑ Vollmann , 8.1


















