Orbit
As orbit or Orbit ( borrowed on English orbit from latin Orbis for "[circle] web") is referred to in astronomy the trajectory, a on the object due to the gravitation in a free fall periodically moved to another object, the central body .
If both objects are assumed to be punctiform and the mutual attraction can be described undisturbed by Newton's law of gravitation , the path has the shape of an ellipse . This also applies to the centers of extended objects with spherically symmetrical mass distribution. If the path of one of the objects is described relative to the other, then the other is in a focal point of the ellipse. Viewed from the common center of mass , each of the objects describes an ellipse, the center of mass being the focal point in both ellipses. When additional forces from outside on such a two-body systemact, or the force does not exactly follow Newton's law of gravity, the - disturbed - orbit shape cannot be a mathematically exact ellipse (see e.g. the perihelion of Mercury ).
The orbit in an orbit is also known as a revolution (see De revolutionibus orbium coelestium ). The time required for this is the period of revolution (or revolution period).
Orbit as a two-body problem

In the two-body system , all influences from other bodies are neglected or, at best, viewed as a small disturbance. This is a good approximation for pairs of orbiting objects such as:
- the earth around the sun ; see earth orbit
- the earth around the earth-moon center of gravity
-
Earth orbit :
- the moon around the earth (or around the earth-moon center of gravity ); see lunar orbit
- Satellite , space shuttle or similar spacecraft ; see satellite orbit
- Planets , comets or asteroids (planetoids) around the sun (for an overview see solar system )
- Moons around other planets or around asteroids
- Double stars around each other (or around their barycentre ).
- Exoplanets around their central object
- the sun (and with it the whole solar system) around the center of the Milky Way
The lanes are Keplerian orbits , so web ellipses with characteristic periodic times that on the average orbital radius and the mass yield of the objects. If there is a considerable difference in masses, the one with the larger one is approximately regarded as the central body around which the other object encircles. The circulation takes place in a plane in which the barycentre of the two bodies is also located. The vector that points from the central object to the revolving object is called the radius vector .
However, even in the two-body system, not all orbits are closed or stable over time. Cometary orbits can be elongated like hyperbolas , and multiple stars or asteroids can find themselves on unstable orbits. The orbit of all stars around the galactic center resembles a spiral rotation with a period of 100 to 300 million years. Relativistic disturbances mean that a Kepler orbit is an idealized case. In fact, all orbits are unstable, including those of the earth, with the greatest disturbances usually being caused by the gravity of other celestial bodies.
Planets, orbital elements, binary stars

The orbits of the planets in the solar system are best known . At the beginning of the 17th century, Johannes Kepler recognized when analyzing the orbit of Mars that these orbits are ellipses (see Kepler's laws ). The same applies to all celestial bodies that move around the sun and are not exposed to any other forces (such as the solar wind ).
From Newton's law of gravitation one can deduce that in every two-body system the orbits are conic sections - that is, circles , ellipses, parabolas or hyperbolas .
With moving point masses in a vacuum , they can be described exactly by six path elements .
The true orbits, however, deviate from these ideal Kepler ellipses , because in principle they are also subject to the gravitation of all other bodies in the system . As long as the bodies are far enough apart, the differences to the idealized conic sections remain minimal. These orbital disturbances can be determined by the disturbance calculation of the celestial mechanics , which goes back to Carl Friedrich Gauß and some of his contemporaries. It models the individual forces and calculates how the current Kepler ellipse merges into the next ellipse in an oscillating manner .
In addition, every uneven mass distribution - such as the flattening of rotating planets - causes a somewhat inhomogeneous gravitational field; this is particularly noticeable in the slightly changed orbits of their moons . Other minor changes to the orbits are described by general relativity .
For example, the planet Mercury shows a small but measurable deviation from an elliptical orbit. After one circuit, it does not come back exactly to the starting point, but rather follows a rosette path by turning the apsidal line in a right-hand direction. The Newtonian theory of gravity can explain this perihelion rotation , but not completely. To do this, the sun would have to have a somewhat flattened shape. The general theory of relativity provides a sufficient explanation for the total size of the perihelion rotation of all planets concerned.
Also binaries follow approached the Kepler's laws, if you understand their movement as two ellipses around the common center of gravity. Special methods of perturbation calculation are only required for multiple systems or very close pairs of stars.
The orbits of two closely orbiting neutron stars show even greater instabilities . The effects of space-time relativity create gravitational radiation and the neutron stars collapse (after a long time) into one another. Numerous X-ray sources in the sky can be explained in this way.
When physicists began to calculate the orbits of electrons in atoms at the turn of the century , they thought of a planetary system on a small scale . The first models were Kepler orbits of electrons around the atomic nucleus .
However, it was soon recognized that electrons orbiting around the nucleus, according to Maxwell's equations, emit electromagnetic waves and, because of the energy emitted in this way , should crash into the atomic nucleus in fractions of a second. This was one of the problems that eventually led to the development of quantum mechanics .
Clear explanation based on the conic cut paths
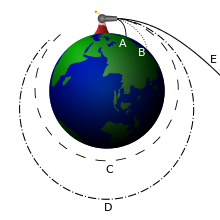
The mechanics of an orbit is often demonstrated using a vivid thought experiment : One assumes that one is standing on a high tower or mountain and firing a projectile horizontally. The air resistance is left out for the time being for the sake of simplicity. The thought experiment becomes even clearer if it is not held on earth, but on a small planet or moon, in the manner of the well-known cover picture of the book The Little Prince or on the Martian moon Phobos (see also below).
- At a low launch speed , the projectile flies along a trajectory parabola and hits the ground after a short flight (path A in the adjacent sketch).
- At higher launch speeds, the parabola turns into an elliptical arc , and the projectile only hits the earth's surface again after it has flown over a noticeable part of the earth's circumference (path B).
- If the launch speed reaches the first cosmic speed , the elliptical arc becomes a full circle , an orbit. So the projectile is too fast to fall down again; it is said that it then "falls around the earth" (Lane C).
- If the launch speed is increased further, the circle becomes an elliptical orbit , with the launch point being and remaining the closest point to the earth (path D).
- If the launch speed exceeds the second cosmic speed, the ellipse opens into a hyperbola . There is no orbit because the projectile is faster than the earth can pull the projectile back towards itself. In other words: the kinetic energy of the projectile is greater than the gravitational energy that the earth acts on the projectile. (Lane E)
Low orbits
If the orbit diameter is only slightly larger than the diameter of the central body, one speaks of a near-surface or low orbit , technically a LEO for Low Earth Orbit . If the central body and the orbit are assumed to be circular with the same radius, equating the weight force with the centrifugal force results for the speed of rotation (the first cosmic speed ) and time of rotation.
with = weight force , = gravitational constant , = mass of the satellite, = mass of the central body, = radius of the central body
The weight of the satellite results when the density of the central body is assumed to be constant and the mass is calculated from this as follows:
By equating it with the expression for the weight force, the centripetal acceleration results (in the case of the earth, the acceleration due to gravity ):
The weight force and the centrifugal force at path speed should ( ) be in equilibrium:
Since the mass of the satellite stands out from this equation, its orbit is independent of its mass, as well as its shape.
Resolved after abbreviation of :
The cycle time results from , i.e. scope / speed:
Apart from natural constants, the orbital time of satellites depends only on the density of the central body, but not on its radius.
Concrete values for orbits around the earth:
The value of about 90 minutes is known as a rule of thumb from low satellite orbits and from most manned orbiting spacecraft.
To compare the Martian moon Phobos :
Although Phobos is only about 25 kilometers in diameter, the orbital time for a near-surface orbit is very similar to that on Earth (and even larger). The orbit speed on this orbit, on the other hand, is only around 33 kilometers per hour . So an astronaut on the Phobos surface could theoretically throw a ball out of hand into orbit. Since Phobos deviates strongly from the spherical shape, the formulas for orbits close to the surface are not suitable in practice here.
The fact that the orbit time for a near-surface orbit is independent of the radius of the central body can be generalized: If a central body has a similar average density to the earth, i.e. if it is roughly structured as "rocky", then the orbital period is like that of the earth In the order of 90 minutes, whether it is an asteroid or an exo-planet around a completely different star.
Earth orbits
In an orbit, the gravitational force of the earth and the centrifugal force cancel each other out in the local co-moving coordinate system . Therefore there is weightlessness on board a spacecraft that is in orbit (see also microgravity ). Most space flights take place in low orbits (a few 100 km) around the earth (e.g. space shuttle missions). For physical reasons, the orbital speed increases or decreases according to the distance to the earth. The geostationary orbit is of particular importance - at an altitude of around 35,800 km and without an incline towards the equatorial plane . Satellites in such an orbit stand still relative to the earth's surface , which is particularly necessary for communication satellites and weather satellites .
See also
- Box orbit
- Orbit determination
- Orbital disruption , discovery of Neptune (planet)
- Quasi-satellite
- Trajectory (physics)
- Vis-Viva equation
- Earth orbit
Web links
Individual evidence
- ^ Orbit - Duden , Bibliographisches Institut ; 2016



























