Position vector

Two points and their position vectors

Position vectors (here denoted by and ) in the Cartesian coordinate system ${\displaystyle {\vec {r}}_{P}}$ ${\displaystyle {\vec {r}}_{Q}}$

In mathematics and in physics, a position vector (also radius vector or position vector ) of a point is a vector that points from a fixed reference point to this point (location). In elementary and synthetic geometry , these vectors can be defined as classes of arrows with the same displacement or as parallel displacements .

Position vectors make it possible to use vector calculation for the description of points , sets of points and images . If a Cartesian coordinate system is used as a basis, the origin of the coordinates is generally chosen as the reference point for the position vectors of the points. In this case the coordinates of a point with respect to this coordinate system coincide with the coordinates of its position vector.

In analytical geometry , position vectors are used to describe images of an affine or Euclidean space and to describe sets of points (such as straight lines and planes ) by means of equations and parametric representations .

In physics , position vectors are used to describe the location of a body in Euclidean space. In coordinate transformations, position vectors show a different transformation behavior than covariant vectors .

Spellings

In geometry, the reference point (origin) is usually referred to as (for Latin origo ). The notation for the position vector of a point is then: ${\displaystyle O}$ ${\displaystyle P}$

${\displaystyle {\overrightarrow {OP}}}$

Occasionally the lowercase letters with vector arrows are also used, which correspond to the uppercase letters with which the points are designated, for example:

${\displaystyle {\vec {p}}={\overrightarrow {OP}},\ {\vec {q}}={\overrightarrow {OQ}},\ {\vec {a}}={\overrightarrow {OA}},\ {\vec {b}}={\overrightarrow {OB}},\ \dots ,\ {\vec {x}}={\overrightarrow {OX}}}$

The notation that the capital letter denoting the point is provided with a vector arrow is also common:

${\displaystyle {\vec {P}}={\overrightarrow {OP}},\ {\vec {Q}}={\overrightarrow {OQ}},\ {\vec {A}}={\overrightarrow {OA}},\ {\vec {B}}={\overrightarrow {OB}},\ \dots ,\ {\vec {X}}={\overrightarrow {OX}}}$

In physics in particular, the position vector is also called the radius vector and is written with a vector arrow as or (especially in theoretical physics) in semi-bold as . ${\displaystyle {\vec {r}}}$ ${\displaystyle \mathbf {r} }$

Examples and applications in geometry

Connection vector

For the connection vector of two points and with the position vectors and the following applies: ${\displaystyle {\overrightarrow {PQ}}}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle {\vec {p}}={\overrightarrow {OP}}}$ ${\displaystyle {\vec {q}}={\overrightarrow {OQ}}}$

${\displaystyle {\overrightarrow {PQ}}={\overrightarrow {OQ}}-{\overrightarrow {OP}}={\vec {q}}-{\vec {p}}}$

Cartesian coordinates

The following applies to the coordinates of the position vector of the point with the coordinates : ${\displaystyle {\overrightarrow {OP}}}$ ${\displaystyle P}$ ${\displaystyle (p_{1},p_{2},p_{3})}$

${\displaystyle {\overrightarrow {OP}}={\begin{pmatrix}p_{1}\\p_{2}\\p_{3}\end{pmatrix}}}$

shift

A shift around the vector maps the point onto the point . Then the following applies to the position vectors: ${\displaystyle {\vec {v}}}$ ${\displaystyle X}$ ${\displaystyle X^{\prime }}$

${\displaystyle {\overrightarrow {OX'}}={\overrightarrow {OX}}+{\vec {v}}}$

${\displaystyle {\vec {x}}'={\vec {x}}+{\vec {v}}}$

Rotation around the origin

A rotation in the plane with the center of rotation to the angle counter -clockwise , with the aid of a as follows in Cartesian coordinate rotation matrix will be described: If the position vector of a point and the position vector of the pixel , then: ${\displaystyle O}$ ${\displaystyle \varphi }$ ${\displaystyle {\vec {x}}={\tbinom {x_{1}}{x_{2}}}={\overrightarrow {OX}}}$ ${\displaystyle X}$ ${\displaystyle {\vec {x}}'={\tbinom {x_{1}'}{x_{2}'}}={\overrightarrow {OX'}}}$ ${\displaystyle X'}$

${\displaystyle {\begin{pmatrix}x_{1}'\\x_{2}'\end{pmatrix}}={\begin{pmatrix}\cos \varphi &-\sin \varphi \\\sin \varphi &\cos \varphi \end{pmatrix}}{\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}}$

Affine figure

A general affine mapping that maps the point to the point can be represented with position vectors as follows: ${\displaystyle X}$ ${\displaystyle X'}$

${\displaystyle {\vec {x}}'=L({\vec {x}})+{\vec {v}}}$

Here, the position vector von , the position vector von , is a linear mapping and a vector that describes a displacement. In Cartesian coordinates, the linear mapping can be represented by a matrix and the following applies: ${\displaystyle {\vec {x}}}$ ${\displaystyle X}$ ${\displaystyle {\vec {x}}'}$ ${\displaystyle X'}$ ${\displaystyle L}$ ${\displaystyle {\vec {v}}}$ ${\displaystyle L}$ ${\displaystyle A}$

${\displaystyle {\vec {x}}=A\cdot {\vec {x}}+{\vec {v}}}$

In three-dimensional space this results in:

${\displaystyle {\begin{pmatrix}x_{1}'\\x_{2}'\\x_{3}'\end{pmatrix}}={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}}\,{\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}+{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}}$

Corresponding representations are also available for other dimensions.

Parametric representation of a straight line

The straight line through the points and contains exactly those points whose position vector is the representation ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle X}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {x}}={\overrightarrow {OP}}+t\,{\overrightarrow {PQ}}}$ With ${\displaystyle t\in \mathbb {R} }$

owns. One speaks here of the parametric form of a straight line equation .

Normal form of the plane equation

The plane through the point (support point) with normal vector contains exactly those points whose position vector corresponds to the normal equation ${\displaystyle P}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle X}$ ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}}$

Fulfills. It is the position vector ( support vector ) of the support point and the Malpunkt denotes the scalar product . ${\displaystyle {\vec {p}}}$ ${\displaystyle P}$

Position vector in different coordinate systems

Cartesian coordinate system

The point described by a position vector can be expressed by the coordinates of a coordinate system, the reference point of the position vector usually being placed in the coordinate origin .

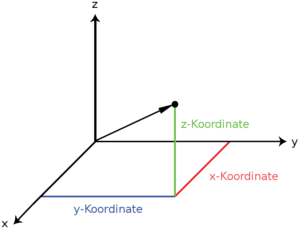
Cartesian coordinates

Usually the position vector is in Cartesian coordinates in the form

${\displaystyle {\vec {r}}={\vec {r}}\,(x,y,z)={\begin{pmatrix}x\\y\\z\end{pmatrix}}}$

Are defined. Therefore the Cartesian coordinates are also the components of the position vector.

Cylindrical coordinates

The position vector as a function of cylinder coordinates is obtained by converting the cylinder coordinates into the corresponding Cartesian coordinates

${\displaystyle {\vec {r}}={\vec {r}}\,(\rho ,\varphi ,z)={\begin{pmatrix}\rho \,\cos \varphi \\\rho \,\sin \varphi \\z\end{pmatrix}}.}$

Here denotes the distance of the point from the -axis, the angle is counted from the -axis in the direction of the -axis. and are therefore the polar coordinates of the point projected orthogonally onto the - plane. ${\displaystyle \rho }$ ${\displaystyle z}$ ${\displaystyle \phi }$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \rho }$ ${\displaystyle \varphi }$ ${\displaystyle x}$ ${\displaystyle y}$

From a mathematical point of view, the mapping (function) that assigns the Cartesian coordinates of the position vector to the cylinder coordinates is considered here . ${\displaystyle (\rho ,\varphi ,z)}$ ${\displaystyle (x,y,z)}$

Spherical coordinates

The position vector as a function of spherical coordinates is obtained by converting the spherical coordinates into the corresponding Cartesian coordinates

${\displaystyle {\vec {r}}={\vec {r}}\,(r,\theta ,\varphi )={\begin{pmatrix}r\,\sin \theta \,\cos \varphi \\r\,\sin \theta \,\sin \varphi \\r\,\cos \theta \end{pmatrix}}.}$

Here denotes the distance of the point from the origin (i.e. the length of the position vector), the angle is measured in the - -plane from the -axis in the direction of the -axis, the angle is the angle between the -axis and the position vector. ${\displaystyle r}$ ${\displaystyle \varphi }$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \theta }$ ${\displaystyle z}$

physics

Celestial mechanics

In order to indicate the position of a celestial body moving on an orbit around a center of gravity , this center of gravity is selected as the origin of the location or radius vector in celestial mechanics . The radius vector then always lies in the direction of the gravitational line . The path of the position vector is called the driving beam . The driving beam plays a central role in Kepler's second law (area theorem) .

See also

• Unit vector
• Frenet's formulas
• Hodograph

Individual evidence

1. ↑ Istvan Szabó : Introduction to Technical Mechanics. Springer, 1999, ISBN 3-540-44248-0 , p. 12.

literature

• Klaus Desch: Mathematical Supplements to Physics II, Chapter 11: Vector Analysis. (PDF, 210 kB). Institute for Experimental Physics, Hamburg.