Elongation (astronomy)
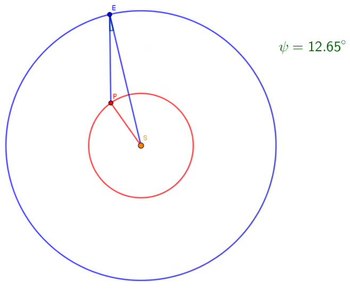
In astronomy, elongation is the angular distance between two celestial objects as seen by an observer . In general, the observer is standing on earth , and elongation describes the observed ( apparent ) distance of a planet from the sun .
The elongation is measured west and east of the sun from 0 ° to 180 °. Western elongation means the object rises in front of the sun and can be seen in the morning sky; when elongated to the east it sets after the sun and can be observed in the evening sky.
On the problem of definition
Two different definitions of elongation are used:
- The (“ geocentric ”) spherical angular distance between a planet and the sun as seen from the center of the earth , measured along the plane in which the planet, the earth and the sun lie.
-
, so
- R … geocentric position vector from the earth to the sun
- g ... geocentric position vector from the earth to the planet
- This angle is opposite to the phase angle in the triangle earth-planet-sun, and the following applies:
-
, so
- The difference in the geocentric ecliptical lengths of the planet and the sun.
-
- λ ... geocentric ecliptical longitude
- With
-
For objects close to the ecliptic and large angular distances, the difference between the two definitions is small except for the sign . However, if the planet is apparently close to the sun, the angles given by the two definitions can differ considerably.
Elongation is one of the classic angles in observational astronomy and has been used since Leonhard Euler . The name is a scientific Latin education to ex- and Latin longus 'lang', also English. elongation means 'stretching, change in length' (rheol., tech., med.), but is used in astronomy in the sense of 'deflection' (a celestial body revolving around its center). This is how you specify the greatest elongation , i.e. the maximum angular distance a planet can have when viewed from outside its orbit.
The elongation is particularly suitable for the perturbation theory because they parameterised the influences of other bodies in the system simple, and can be found as such the late 19th century in the planetary theory of Hill and Newcomb as well as the lunar theory to Brown (ILE). However, these theories neglected the existing, albeit small, ecliptical latitudes of the sun and the individual planets, so that spherical and ecliptical angular spacing coincided. As an orbit element in the lunar theory according to Brown- Eckert (j = 2) one goes over to the Delaunay parameter for the mean elongation, which is measured as a broken angle ecliptically from the sun to the lunar node , and from there in the lunar orbit plane to the moon .
Careless use of the term elongation in specialist literature has led to this unsatisfactory definition. The first - ecliptical - definition is used, for example, by the Astronomical Almanac , the second - spherical - by the Annuaire du Bureau des Longitudes , among others , the third - as a broken angle - in the lunar theory, which, however, hardly played a role until the development of modern computer astronomy : Relevant calculation accuracies and the visual precision to control them were only achieved in the 1980s.
The deviation causes problems in particular in the measurement of the exact times of conjunction and opposition , the classic definition of which is. Draws a planet for a terrestrial observer apparently behind the sun passed (conjunction), or in front of it (passage), he incurs due to the inclination of its orbit to the ecliptic above or below the Sun's middle over. The elongation according to the second definition always assumes the value zero at a certain point in time, since the geocentric lengths of planet and sun must necessarily coincide during this process - if the sun and planet center lie in a normal plane on the ecliptic. The elongation according to the first definition, on the other hand, only decreases to a certain minimum value and then increases again - namely the angular distance at the moment of closest approach . It would only take on the value zero if the planet center ran exactly through the center of the sun disk - which exactly does not happen in nature. The same applies to the opposition of a planet: the elongation according to the second definition always takes the value 180 ° for a moment when it changes from west to east. The elongation according to the first definition usually does not reach this value.
Therefore, there are still different information for the two aspects in the literature. Usually the conjunction is indicated with (geocentric- ecliptical ), or also (i.e. geocentric- equatorial ), functions which, although they become exact zero, do not describe the exact point in time of maximum proximity, but elsewhere with (geocentric or topocentric- spherical) or in relation to the lunar theory with (broken ecliptical / orbit system), which typically have no zero. This has caused confusion, especially when the moon passes near the node, i.e. when it comes to the criteria for a solar eclipse .
The error has only been noticed since zero point searches failed due to today's high computational accuracy or, on the other hand, expressions about the angular distance in computer programs produced crashes because an exact zero appeared where none should be. Therefore, in more recent publications the reference plane is explicitly mentioned, or the term elongation is avoided, the new lunar theory ELP2000, for example, explicitly speaks of argument instead of ' elongation ' - with 'argument' as an expression of celestial mechanics for unspecific, more detailed parameters. In the case of older literature, it is often not easy to find out which definition is used.
Greatest elongation
While the planets (or other celestial bodies) that are outside the earth's orbit ( upper planets ) can be in opposition and thus achieve an elongation of up to 180 °, this does not apply to planets and other celestial bodies whose orbit is within the earth's orbit ( lower planets ). Objects within the earth's orbit can naturally only be within a range of ± 90 °. Venus has a maximum elongation of only 47 °, and Mercury 28 °. The exact value fluctuates, in astronomical yearbooks the times and degrees of the greatest western or eastern elongation are usually given.
Example:
Mercury reached the greatest angular distance from the Sun on August 11, 1990 (namely 27 ° 25 ') at 9 p.m. UT , but the greatest distance in geocentric longitude (27 ° 22') at 3 p.m. UT.
Observation practice
The elongation is decisive for the visibility of an object. However, great elongation does not always mean good visibility. Mercury cannot be observed in summer and autumn in our latitudes with its maximum eastern elongation in the evening sky and in spring and winter with its largest western elongation in the morning sky, although these are greater than the largest eastern elongations in winter or spring and the largest western elongations in summer or autumn, because in our latitudes the ecliptic stands flat to the horizon in summer and autumn in the evening and in winter and spring in the morning and Mercury sets during light twilight or only rises during light twilight.
Even Venus does not achieve its best visibility at the greatest elongation: With it, the contribution made by the proportion of the illuminated disk ( degree of illumination ) is already relevant due to its proximity to earth. In the greatest elongation, however, only about 53% of the disk is illuminated, and it reaches its maximum brightness about five weeks before / after the maximum elongation.
Practical use
By observing the elongation, one can determine the distance between a planet and the sun in our solar system in AE (i.e. relative to the distance between the earth and the sun ). Knowing the relative distances required z. B. Kepler for drawing up the laws named after him . For the sake of simplicity, we assume that all orbits are circular. We designate the sun with , the earth with , the planet with and the distances between the three celestial bodies with , and . There are two cases (lower and upper planet) to be distinguished.
The elongation of a lower planet fluctuates between 0 ° and a value less than 90 ° (see animation for Mercury ). For the maximum value forms a tangent to the orbit of , i. H. . Hence it is right angled and it is
With
surrendered
The distance between an upper planet and the sun cannot be determined by observing the elongation between 0 ° (conjunction of ) and 180 ° (opposition of ). If you also know the cycle time of , there are different approaches, but in principle the same. In the simplest case one starts the observation with the opposition of ( ). Now you count the days until the planet is in quadrature, i.e. H. . At this point in time the position of the earth is denoted by , that of the planet by (see animation for Jupiter ). If we denote the angles , then these are in the same relationship to the full circle as to the associated cycle times:
Be it . Because of that we can calculate this angle:
In right-angled it applies
With the knowledge of and we get the distance between the planet and the sun
See also
- Constellation (aspect)
- Syzygium
- Biggest digression
Individual evidence
- ↑ PK Seidelmann (Ed.): Explanatory Supplement to the Astronomical Almanac . University Science Books, Mill Valley 1992, ISBN 0-935702-68-7 , pp. 34, 726 (English).
- ↑ Andreas Guthmann: Introduction to celestial mechanics and ephemeris calculation . BI-Wiss.-Verl., Mannheim 1994, ISBN 3-411-17051-4 , pp. 180 .
- ↑ a b c J. Meeus: Astronomical Algorithms . 2nd Edition. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1 , pp. 253 (English).
- ↑ Entry Elongatio. In: LEO. Retrieved November 18, 2008 .
- ↑ Entry Elongation. In: Meyers Online Lexikon (Zeit Online). Archived from the original on January 12, 2008 ; Retrieved June 21, 2009 .
- ↑ Hermann Mucke: Wandelgestirnorte . In: Modern Astronomical Phenomenology. 20th Sternfreunde Seminar, 1992/93 . Zeiss Planetarium of the City of Vienna and Austrian Astronomical Association , 1992, 6. The movement of the moon around the earth, p. 33-38 (quoted from Jean Meeus : Astronomical Algorithms. ISBN 0-943396-35-2 ).
- ↑ a b Entry Conjunction. In: World of Science - Astronomy. Eric Weisstein , accessed on November 18, 2008 (English, there the definition according to the Bureau des Longitudes is called least separation ).
- ↑ JL Simon, P. Bretagnon, J. Chapront, M. Chapront-Touze, G. Francou, J. Laskar: Numerical expressions for precession formulas and mean elements for the Moon and the planets . In: Astronomy and Astrophysics . No. 282 , 1994, pp. 663-682 (English, reference: p. 671).





![\ psi \ in \,] 0.180 [](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ca70b151e063b489450655fe699693a9304b9e0)

![\ psi \ in \; ] -180, 180]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d73b58e59a179d8910747d7512a2797ec77cca8f)