Apparent brightness
The apparent brightness indicates how bright star or other celestial body to an observer on the earth in comparison to appear . This astronomical comparison value is described using a logarithmic scale and given as a number with the addition of magnitude , mag for short (also m ), size class or simply size .
Stars of the 1st magnitude appear brighter than stars of the 2nd or 3rd magnitude and are given a lower numerical value for their magnitude (mag) on this scale . The lower the value on this scale, the greater the apparent brightness of a star; particularly bright objects have a negative mag value.
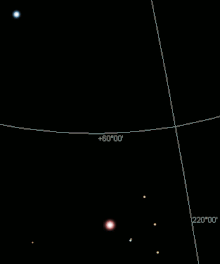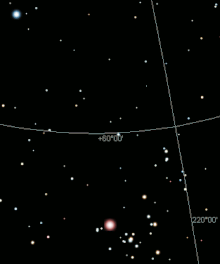
visibility up to 4 mag over a big city;
Visibility 6 likes without light pollution
The original 6-point brightness scale is first documented in Ptolemy of Alexandria in the star catalog of the Almagest (2nd century AD). The claim that it was used earlier by Hipparchus of Nicaea (2nd century BC, exact dates of life unclear) cannot be substantiated or refuted because the star catalog of Hipparchus, whose former existence is told by Pliny the Elder. Ä . and Ptolemy has come down to us, has not survived. The only surviving script by Hipparchus, a commentary on the didactic poem Aratos , provides very precise position information, but clearly indicates the absence of a magnitude scale, since the brightness of stars (if at all) is only given with words (large / small) or is transmitted through the indication that these stars are visible even with a full moon. Claims that the magnitude scale goes back to Babylonian astronomy date back to the time of Panbabylonism and cannot be substantiated in the texts of mathematical Babylonian astronomy [cf. Editions of the Babylonian Astronomical Diaries]. The earliest evidence of the magnitude scale (which may not have survived models) is the star catalog in the Almagest (2nd century AD). There the freely visible stars are divided into six size classes, but without describing the method of this determination in more detail. The brightest stars were assigned to the first magnitude, the weakest to the sixth magnitude.
Later the scale was expanded on both sides in order to be able to classify both lighter objects and - after the advent of the telescope - weaker objects. Today's scale of apparent brightness is logarithmic according to the sensory perception (see Weber-Fechner law ). It was defined by Norman Pogson in 1850 in such a way that a first magnitude star with 1.0 mag is exactly 100 times as bright as a star sixth magnitude with 6.0 mag, and this one hundred times brighter than a star with 11.0 mag, which is thus ten thousand times darker than the 1.0 mag. (Like) a size difference of 1 magnitude thus corresponds to a difference in brightness by a factor or an exposure range of exposure value steps. The scale was calibrated using so-called standard stars .
The observability of an astronomical object depends on various factors - surface brightness of the object, observation conditions ( light pollution ), light-gathering ability of the instrument, spectral sensitivity. The apparent brightness of a star in the range of visible light is only part of the overall performance ( bolometric brightness ). In this way, an object can appear brighter on another observation band, for example in the infrared range. A number of different filter systems have been defined for scientific observation purposes, which can be used to compare observations with different telescopes and instruments. In contrast to brightnesses measured photographically or photoelectrically with a different spectral sensitivity, that apparent brightness as it appears to the human eye with visual perception is referred to as visual brightness .
The apparent visual brightness depends on the distance of the earth or the observer from the observed object and in the case of non-luminous objects - such as planets , dwarf planets , asteroids , trans-Neptunian objects and others - additionally on the phase and the distance to the central star. Because of its proximity to the full moon , the moon appears much brighter than distant stars, although they shine billions of times more strongly.
The so-called absolute brightness is used as an auxiliary variable for comparing the actual luminosity of celestial objects . They each equivalent to the brightness of an object that can be seen from a distance of 10 parsecs (about 32.6 light years , about 308.6 trillion kilometers) would be watching. At this distance our sun would appear with an (absolute) visual magnitude of 4.84 mag as a star of only 5th magnitude; From the mean distance earth-sun (1 AU ), however, it is by far the brightest object in the sky with almost −27 mag.
| Surname | Object type | Maximum observed magnitude |
|---|---|---|
| Sun | star | −26.73 mag |
| Sun as seen from Neptune |
star | −19.35 mag |
| Full moon | moon | −12.73 mag |
| Iridium flare | satellite | −9 likes |
| ISS | Space station | −5 likes |
| Venus | planet | −4.67 mag |
| Jupiter | planet | −2.94 mag |
| Mars | planet | −2.91 mag |
| Mercury | planet | −1.9 mag |
| Sirius | star | −1.46 mag |
| Canopus | star | −0.73 mag |
| Saturn | planet | −0.47 mag |
| Vega | star | 0.03 mag |
| Pole Star | star | 1.97 likes |
| Andromeda | Galaxy | 3.4 likes |
| Uranus | planet | 5.5 mag |
| (1) Ceres | Dwarf planet | 6.6 likes |
| Neptune | planet | 7.8 likes |
| (134340) Pluto | Dwarf planet | 13.9 likes |
| (136199) Eris | Dwarf planet | 18.8 mag |
| S Ori 70 | Planemo | 20.8 mag |
Spellings
The Pole Star has an apparent magnitude of about two. The following spellings are common for this:
- 2.0 m
- 2 0
- 2.0 mag
- 2. Magnitude
- m = 2.0
- Star 2nd magnitude
- Size class 2
- 2nd magnitude class
The International Astronomical Union recommends the spelling 2.0 mag as a unit symbol and advises against using a superscript m. However, the author Hans-Ulrich Keller is of the opinion that "mag" is used in popular scientific literature, but in professional astronomy the notation with a superscript m after the integer value is common. (2nd variant from above)
definition
According to Norman Robert Pogson , a difference in brightness of 1: 100 corresponds to a difference of five size classes or 5 mag. The magnitude scale is logarithmic , just as sensory perceptions in humans are proportional to the logarithm of the stimulus according to the Weber-Fechner law .
Physically , the brightness scale is defined by the energy of the incident light ( bolometric brightness ). If the magnitudes and the measured luminous fluxes are two celestial bodies, then applies to their brightness difference
- ,
where the function corresponds to the decadic logarithm (to base 10), which can be simplified too .
If the luminous flux of an object of size class 0 is taken, the brightness of the first object is obtained
For small variations in brightness (i.e. ) approximately applies
The quotients of the constants appearing here are (both representations clarify the connection with the definition)
- and .
The ratio of the brightness of class m to the brightness of class ( m +1) is
For example, a relative brightness difference of 1 ppm corresponds to a brightness class difference of approximately 1.1 µmag.
Photometric zero point
With the beginning of photometry , the individual classes were further subdivided; almost any refinement is possible for modern measuring instruments . An exact reference value became necessary. Initially, the scale on the North Star was aligned with 2.1 mag, until it turned out that its brightness varied slightly. The star Wega , whose brightness was fixed at zero magnitude, traditionally serves as a reference . Today, a group of precisely measured reference stars near the celestial pole , the so-called “ pole sequence ”, is used to calibrate modern photometric systems . The frequently used UBV system is calibrated in this way, for example. This results in an apparent brightness of V = + 0.03 mag for Wega in the UBV system . Color indices are defined in such a way that stars of type A0V (Wega belongs to them) have an average color index of 0.00. Brightness systems with this property are called "Wega brightnesses".
Furthermore, the apparent brightness depends on the wavelength of the light. Therefore, in observational astronomy, the apparent brightness is often given for the visual spectral range around 550 nanometers . It is identified by the symbol V. Other common ranges for optical telescopes are U ( ultraviolet , 365 nm), B (blue, 445 nm), R (red, 658 nm), I, J, H and K (near infrared, 806 to 2190 nm).
The Gaia mission cannot measure stars with a magnitude brighter than 3 in the usual way and can only deal with stars brighter than 7 to a limited extent, so the pole sequence is not suitable for calibration. For the calibration, a new list of approx. 200 reference stars of different spectral classes was used, which form the Gaia Spectrometric Standard Catalog (SPSS) . The vast majority of these objects have a magnitude between 10 and 15.5. Gaia uses its own definition of magnitude called G-band magnitude or G-magnitude (G) in short. Gaia is a self-calibrating mission, so the different catalogs use different definitions for magnitude.
Illuminance
An object of apparent visual brightness causes an illuminance of
Sirius ( m v = −1.46 mag), for example, causes an illumination of 8 μlx .
Total brightness of multiple stars
The total brightness of a multiple star is calculated from the luminous flux of the individual components:
In the case of a double star (n = 2) with the magnitudes m 1 and m 2 of the individual components, one obtains:
Comets
The apparent brightness of comets can be described by:
Where:
- m 0 : Brightness that the comet would have if it were exactly at a distance of 1 AU to the earth and the sun
- Δ: Distance to earth in units of AU
- The factor 2 results from the quadratic dependence on the distance
- n : Change in brightness when the distance from the sun changes. Without interaction it is 2.
- r : distance to the sun in units of AU
m 0 and n are fit parameters that are derived from measurements and allow a comparison of the comets with one another. For example, the brightness curve of the comet Tempel 1 with the parameters m 0 = 5.5 mag and n = 25 could be reproduced quite well.
Performance limit of an optical instrument
In a heavily light-polluted sky, such as that over a large city, even the dark-adapted eye can only see objects up to 4 mag, under less unfavorable circumstances in the country up to 6 mag. Under ideal conditions without light pollution, in addition to the zodiacal light and the counter- light, fainter stars above 7 mag up to 8 mag can be observed with the naked eye in the night-black sky (see also Bortle scale ).
More stars can be seen with observation devices; the apparent brightness of the weakest barely recognizable determines the limit size . In this regard, the performance of telescopes with the opening D can be estimated by comparing them with the pupil opening d . How many size classes the instrumental limit size is above the free-eyed limit size results from the ratio D / d (and since the opening area depends quadratically on the diameter, the logarithmic definition equation gives the factor 2):
If one takes a limit size of 6 mag as a basis for observation with the naked eye and a pupil diameter of d = 7 mm, one obtains:
The relationship can be simplified because :
A binocular with an aperture of 20 mm extends visibility by a good two size classes, a telescope of 70 mm by five, in the example up to 11 mag and one from 200 mm to 13 mag. Large telescopes with CCD sensors are advancing to size classes of 30 mag. The current instrumentation of the Hubble Space Telescope still sees stars of the 31st magnitude.
The apparent brightness in practice
Observability with the naked eye
The apparent brightness of the sun, its planets and our moon fluctuates, partly because of their variable distance from the earth. The magnitude can be even more dependent on the phase of celestial objects such as the moon that do not illuminate themselves (crescent moon around new moon). Some stars also show changes in their apparent brightness over relatively short periods of time. However, the reason for this is not fluctuations in distance, but changes in the light emission of these radiation sources or their coverage by other celestial bodies. For such variable stars an apparent brightness is given as a fluctuation range within the observed limits.

It should also be noted that certain celestial objects such as the Andromeda galaxy (3.5 mag) are objects whose overall brightness is assigned to a larger area of the sky. Therefore, observing the Andromeda Galaxy requires good visibility conditions, while a star like Iota Cephei (3.6 mag) , for example , can still be seen from cities.
The clear-sighted stars are distributed as follows - with the Henry Draper catalog as a comparison:
| Number of stars | Size class | Magnitude | comment |
|---|---|---|---|
| 22nd | 1 | ≤ 1.5 | 22 stars without sun (→ list ) |
| 70 | 2 | 1.5 < x ≤ 2.5 | (→ list ) |
| 170 | 3 | ||
| 430 | 4th | to Argelander / Kapteyn | |
| 1,200 | 5 | ||
| 4,000 | 6th | ||
| 9.110 | <6.5 | According to Bright Star Catalog (1908) | |
| 11,713 | <7.1 | Extended version of the Bright Star catalog ("Harvard Revised", 1983) | |
| 359.083 | <9.0 | Henry Draper Catalog (1949) |
The Flamsteed catalog lists 2,554 stars that were visible to the naked eye from the south of England when the catalog was created. The most distant, freely visible stars of our Milky Way include the variable VV Cephei A and RW Cephei as well as μ Cep, the garnet star , and ν Cep (4.29 mag, 4700 ly) - all in the constellation Cepheus - also P Cygni ( currently around 4.82 mag, about 6000 light-years away) in the swan . The pistol star in the constellation Sagittarius ( Sagittarius ), 25,000 light-years away , only appears between 7.1 and 7.6 mag, as it is covered by the pistol nebula.
The most distant, freely visible permanent objects are neighboring galaxies: In the northern sky the Andromeda Nebula (M 31) in 2.5 million light years with 3.5 mag and, under very good conditions, the Triangle Nebula (M 33) in 2.8 million light years away 5.7 mag and - under extremely favorable conditions - for very good observers, in addition, Bodes Galaxie (M 81) with 6.9 mag, 12 million ly away. In the southern sky , the Large and Small Magellanic Clouds at 160,000 ly and 200,000 ly away respectively are quite bright objects with 0.9 mag and 2.7 mag and belong to the local group as satellite galaxies of the Milky Way , the galaxy 12 million ly away Centaurus A with 6.6 mag is part of the M83 group , which also includes the southern firewheel galaxy (M 83) with 7.5 mag.
Special objects
In addition to the "classic" celestial objects, there are some other objects that only appear conspicuously for a short time or can only be seen in certain places on earth. They can even surpass the brightness of Venus.
| object | root cause | Sample event | like. Max | Duration |
|---|---|---|---|---|
| Meteor in the earth's atmosphere | Particles in the atmosphere are made to glow | Lugo - Bolide | −23 likes | |
| comet | Reflection of the sunlight on the dust tail |
Great September Comet , Comet Ikeya-Seki |
−17 likes | |
| Artificial satellites | Reflection of the sunlight |
Iridium Flare Iridium satellites |
−9 likes | up to several minutes |
| International space station | −5 likes | |||
| Supernova explosion | Sudden release of energy | Supernova 1006 | −9 likes | 17 days |
| Gamma-ray burst | Sudden release of energy | In 2008, GRB 080319B was the most distant, freely visible event with 7.5 billion lj | 5.8 likes | 30 seconds |
Amateur astronomy
With a telescope with an opening diameter of 25 cm, stars up to 14 mag can be observed under good visibility conditions, although this can be improved with astrophotography . Quite a few asteroids and dwarf planets have been observed and discovered by amateur astronomers.
All Messier objects can be observed by amateur astronomers. The quasars 3C 273 (12.9 mag, 2.4 billion light years away) and 3C 48 (16.2 mag, 3.9 billion light years ) are still within the capabilities of amateur astronomers.
Research telescopes
The Keck telescope in Hawaii can detect stars up to 26th magnitude, the Hubble space telescope up to 31. The planned James Webb space telescope is expected to perform up to 34th magnitude in the infrared range. The Vatican Advanced Technology Telescope can classify and characterize trans-Neptunian objects that are weaker than 21 mag according to their color.
In scientific astronomy, the apparent brightness is of paramount importance, because ultimately all the image material obtained using telescopes consists of raster data , with each pixel expressing a certain apparent brightness. These grid data can be evaluated for further (computer-aided) analysis. For example, stars are photographed with two color filters, B (445 nm wavelength, blue light) and V (551 nm, yellow-green area). The distance to the star is known from parallax measurements - this is how the absolute brightness can be calculated and the surface temperature of the star can be calculated from the brightness ratio under the two color filters. From this, the size and evolution of the star can ultimately be estimated.
In contrast to terrestrial telescopes, space telescopes also observe the universe in the infrared range. This radiation penetrates dust and enables the observation of objects that hardly radiate in the visible range, such as planets, gas clouds, brown dwarfs and emerging stars. The Gaia space telescope delivers the G-band magnitude defined for this telescope .
See also
- Absolute brightness , bolometric brightness , luminosity
- Astrophysics , photometry , color index , pole sequence
- List of the brightest stars
- Apparent place
Remarks
- ↑ Defined as 0 in traditional photometric systems; due to calibration difficulties these systems deviate somewhat.
- ↑ In principle, any logarithmic function (on any basis) can be used; here we use the two most common variants (decadic and natural logarithm).
- ↑ Since the function has the slope 1 and the function value 0 at this point, the function for can be approximated by a straight line, and it then applies . Therefore applies to the approximation .
Individual evidence
- ↑ Susanne M Hoffmann: Hipparchs celestial globe . Springer, Wiesbaden / New York 2017, ISBN 978-3-658-18682-1 , pp. 92 and 194 .
- ↑ D. Baker, D. Hardy: Der Kosmos-Sternführer. Franckh-Kosmos, Stuttgart 1981, pp. 32-34.
- ↑ According to E. Zinner, errors of 1–2 mag occur, on average ± 0.6 mag.
- ↑ cf. z. B. Hans-Ulrich Keller: Kosmos Himmelsjahr 2013. Sun, moon and stars in the course of the year. 2013, ISBN 978-3-440-13097-1 .
- ↑ page of the IAU (last section, "5.17 Magnitude")
- ↑ Hans-Ulrich Keller : Compendium of Astronomy: Introduction to the Science of the Universe . 6th, updated and expanded edition. Stuttgart 2019, ISBN 978-3-440-16276-7 , pp. 65 .
- ^ HL Johnson, WW Morgan: Fundamental stellar photometry for standards of spectral type on the revised system of the Yerkes spectra atlas . In: The Astrophysical Journal . tape 117 , 1953, pp. 313-352 .
- ↑ a b Definition of visual brightness
- ^ Jean Dufay: Introduction to Astrophysics: The Stars . Dover Publications, 1964, ISBN 978-0-486-60771-9 ( limited preview in Google Book Search [accessed November 4, 2019]).
- ↑ Florian Freistetter : What is the name of the most distant star that we can still see with the naked eye? October 20, 2014, accessed February 20, 2018 .
- ^ Farthest Naked Eye Object. Retrieved February 20, 2018 .
- ^ Luigi Foschini: On the airbursts of large meteoroids in the Earth's atmosphere. The Lugo bolide: reanalysis of a case study. In: Astronomy and Astrophysics. 337, 1998, pp. L5-L8; arxiv : astro-ph / 9805124
- ↑ Supernova 1006
![{\ displaystyle {\ sqrt [{5}] {100}} \ approx 2 {,} 511886}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fcafe9433a5708a8f64165970693e432108756f)
![{\ displaystyle \ log _ {2} {\ sqrt [{5}] {100}} \ approx 1 {,} 33}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04c08aeffc2494f7ecd578478938291654271b0f)












![{\ frac {{\ text {brightness}} ({\ text {class}} [m])} {{\ text {brightness}} ({\ text {class}} [m + 1])}} = { \ sqrt [{5}] {100}} = 10 ^ {0 {,} 4} \ approx 2 {,} 512](https://wikimedia.org/api/rest_v1/media/math/render/svg/df04ef97829a5960cca79639212fffcb6c39ee03)














