Bessel elements

Outlines of the umbra and penumbra (green) on the earth's surface (gray) and in the fundamental plane (red) during a total solar eclipse

The Bessel elements are geometric quantities that Friedrich Wilhelm Bessel introduced to describe the local conditions during a solar eclipse at an observation location on earth. In addition to solar eclipses, the principle associated with this can also be used for star or planet coverings by the moon and the transits of Venus and Mercury in front of the sun. The calculations made for lunar eclipses are similar to the calculation of the Bessel elements, in which case the shadow does not fall on the earth, but on the moon.

In the case of solar eclipses, for example, based on the Bessel elements, the period of coverage at a certain location can be determined, or the path along which the umbra of the moon sweeps over the surface of the earth can be determined. This calculation method was developed by Bessel in 1829 and later refined by William Chauvenet .

The basic idea of ​​the procedure is that the Bessel elements reproduce the movement of the shadow caused by the covering heavenly bodies - in solar eclipses this is the moon - on an imaginary fundamental plane. This is the geocentric normal plane of the shadow axis, in which the center of the earth lies and which is perpendicular to the axis of the shadow cone. The latter is the straight line that goes through the centers of the covered and the covering celestial body.

To describe the movement of the shadow in this suitably selected plane, it is sufficient to specify a comparatively small number of sizes - with sufficient accuracy. This is not least due to the fact that the shadow is always circular in this plane during the entire course of the eclipse and is not subject to any perspective distortion. In a second step, the values ​​for the earth's surface are calculated by determining the intersection curves of the shadow cones with the earth's surface, whereby only then must the approximately spherical shape of the earth, the rotation of the earth and the position and height of the observation site be taken into account.

history

Friedrich Wilhelm Bessel (1784–1846)

William Chauvenet (1820-1870)

This method of describing the eclipses of stars and planets as well as solar eclipses was developed by the German scientist Friedrich Wilhelm Bessel in the 1820s. Bessel's first work on the subject of star occultations can be found in Astronomical News No. 50 from 1824, in which he made some calculations on the basis of previously observed star occultations. In 1829 he published a generalizing paper on the forecasting of star eclipses in Astronomical News No. 145. In the same year he developed the idea further by generalizing the method with the aim of applying it to planetary eclipses and solar eclipses.

Up to this point in time, two independent methods with different goals were used for the calculation. The first method was used to determine the conditions as they appeared to an observer at a specific location. The method used here went back to Johannes Kepler and was later further developed by Jérôme Lalande and Johann Gottlieb Friedrich von Bohnenberger . The second method, which can be traced back to Joseph-Louis Lagrange , was used to calculate the time of the conjunction . Since this method referred to the center of the earth and could not make any statements about local conditions on the earth's surface, it was used less frequently than the first to calculate eclipses. However, it simplified many other astronomical calculations. Bessel's approach now consisted of further developing Lagrange's method in such a way that the calculation of the local conditions was also possible, with which he achieved a combination of both methods.

In the second volume of his astronomical investigations in 1842 Bessel published a four-section treatise entitled Analysis of the Eclipses . In it he summarized his previously published work on this topic and rounded it off with some additions. This publication served as the basis for many astronomers who later grappled with this topic. In his work Theory of Solar Eclipses and Related Phenomena , published in 1858, Peter Andreas Hansen used the line of intersection of the ecliptic with the fundamental plane as the axis, unlike Bessel . However, Bessel's variant, the use of the equatorial plane instead of the ecliptic, had some advantages, as the American astronomer William Chauvenet pointed out in 1863 . In his Manual of Spherical and Practical Astronomy, he largely followed Bessel's method, but developed his own solution approaches for some sub-problems. Chauvenet's presentation was then the basis for many further developments in this area. ${\displaystyle x}$

Even if the calculations of eclipses are no longer done manually, but electronically, the Bessel elements have not lost their meaning. On the contrary, they represent the link between the calculations of the time of the occurrence of an eclipse and the calculations of the local conditions. Many computer programs specialize in one of the two calculations, with the Bessel elements acting as an interface , so to speak .

Solar eclipses

The mutual covering of stars observable at one place on the earth's surface depends on the orbital data of the covered more distant and the covering closer one. These dates ( ephemeris ) are usually given as angles of right ascension and declination . These angles relate to the center of the earth as geocentric coordinates , so that the celestial cover that can be observed at a certain point on the earth's surface cannot be taken directly from them.

In order to describe the coverage at a point on the earth's surface, the orbit data of the two celestial bodies taken from tables or otherwise known must be converted. The Bessel elements are used to describe the course and the size of the umbra and penumbra in the fundamental level. On the one hand, it is not difficult to describe the course of the shadow in this plane based on the orbital data of the celestial bodies; on the other hand, a very simple conversion to an observation point is also possible. For the latter conversion, the Bessel elements also contain information on how the fundamental plane is rotated with respect to the prime meridian and the equatorial plane .

The covering of the sun by the moon is the most complicated type of occultation with regard to the description of the conditions on earth , since both the covered body - the sun - and the covering body - the moon - have non-negligible viewing angles . In addition, the apparent movement of the sun during the cover must be taken into account.

Definition of the Bessel elements

Fundamental plane with the Bessel elements , , and ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle l_{1}}$ ${\displaystyle l_{2}}$

First, a right-angled coordinate system is introduced, which is referred to as the fundamental or Bessel coordinate system. The starting point is the shadow axis, the straight line connecting the center of the sun and moon. The parallel of the shadow axis , which goes through the center of the earth, represents the axis of Bessel's fundamental coordinate system and constantly follows the shadow, so the coordinate system rotates with the direction of the shadow axis. The fundamental plane is perpendicular to this axis in the center of the earth. In the fundamental level, the position and size of the umbra and penumbra are described by means of the and coordinates. The -axis is the line of intersection of the fundamental plane with the equatorial plane and points to the east, the -axis points to the north. ${\displaystyle z}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$

The first two quantities of the Bessel elements are the coordinates and the intersection of the shadow axis with the fundamental plane. The direction of the shadow axis - which corresponds to the direction of the axis - is given by the declination and the ephemeris hour angle. The radius of the penumbra cone in the fundamental plane is described by , that of the umbra cone by . is negative for a total eclipse, positive for an annular one. The values , , and are usually in units of the equatorial radius given the earth. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle d}$ ${\displaystyle \mu }$ ${\displaystyle l_{1}}$ ${\displaystyle l_{2}}$ ${\displaystyle l_{2}}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle l_{1}}$ ${\displaystyle l_{2}}$

In addition to these six variables, which change in the course of the eclipse, there are two other variables that can be regarded as constant: The sizes and define the half opening angle of the penumbra or umbra cone . ${\displaystyle \tan f_{1}}$ ${\displaystyle \tan f_{2}}$

Calculation of the Bessel elements

The Bessel elements used for solar eclipses are based on the temporal course of the geocentric positions of the sun and moon, which are available via their ephemeris . One way to calculate the occurrence of solar eclipses is to immediately convert the positions of the sun and moon into the fundamental coordinate system. Then it can be determined quite easily whether and when the shadow axis penetrates the fundamental plane within the terrestrial globe - which means that a central, i.e. total or ring-shaped eclipse is occurring.

There are other ways to calculate the occurrence of solar eclipses, for example using the eclipse limit . But also in this case the positions of the sun and moon for the course of the eclipse have to be converted into the fundamental coordinate system in order to be able to calculate local conditions at every place on earth on the basis of the Bessel elements.

Based on the geocentric coordinates and the distances from the sun and moon, the Bessel elements can be calculated for a specific point in time. From the declination and right ascension as well as the distance , the position vectors of the sun and moon can be determined as follows: ${\displaystyle \delta }$ ${\displaystyle \alpha }$ ${\displaystyle r}$

${\displaystyle \mathbf {r} _{s}=r_{s}{\begin{pmatrix}\cos \alpha _{s}\cos \delta _{s}\\\sin \alpha _{s}\cos \delta _{s}\\\sin \delta _{s}\end{pmatrix}}}$

${\displaystyle \mathbf {r} _{m}=r_{m}{\begin{pmatrix}\cos \alpha _{m}\cos \delta _{m}\\\sin \alpha _{m}\cos \delta _{m}\\\sin \delta _{m}\end{pmatrix}}}$

The equatorial radius of the earth is usually used as the unit for the distances. In the literature, distance is often expressed in terms of parallax , which can be found in the ephemeris tablets. Since the parallax is based on the radius of the earth, the distance can be calculated in units of the equatorial radius through . ${\displaystyle P}$ ${\displaystyle r}$ ${\displaystyle r=1/\sin P}$

In the following, the first of the Bessel elements to be calculated are the declination and the ephemeris hour angle, i.e. the equatorial coordinates of the direction of the shadow axis . Instead of the hour angle, the right ascension is first calculated, from which the hour angle can be determined using the formula , whereby the sidereal time related to Greenwich corresponds to. ${\displaystyle d}$ ${\displaystyle \mu }$ ${\displaystyle a}$ ${\displaystyle \mu =\theta -a}$ ${\displaystyle \theta }$

For conversion to the fundamental coordinate system, the unit vectors , and , which point in the direction of the coordinate axes of this coordinate system, are expressed using the two quantities and : ${\displaystyle \mathbf {i} }$ ${\displaystyle \mathbf {j} }$ ${\displaystyle \mathbf {k} }$ ${\displaystyle d}$ ${\displaystyle a}$

${\displaystyle \mathbf {i} ={\begin{pmatrix}-\sin a\\\cos a\\0\end{pmatrix}};\quad \quad \mathbf {j} ={\begin{pmatrix}-\cos a\sin d\\-\sin a\sin d\\\cos d\end{pmatrix}};\quad \quad \mathbf {k} ={\begin{pmatrix}\cos d\cos a\\\cos d\sin a\\\sin d\end{pmatrix}}}$

Position vectors of the sun and moon as well as their difference vector, which corresponds to the -axis ${\displaystyle z}$

Since the direction of the -axis corresponds to the difference between the position vectors from the center of the earth to the sun and moon, the unit vector in the direction of the -axis can also be expressed as follows: ${\displaystyle z}$ ${\displaystyle z}$

${\displaystyle \mathbf {k} ={\frac {\mathbf {r} _{s}-\mathbf {r} _{m}}{|\mathbf {r} _{s}-\mathbf {r} _{m}|}}}$

By equating the two representations of now can be and thus determine all the unit vectors of the fundamental coordinate system. ${\displaystyle \mathbf {k} }$ ${\displaystyle d}$ ${\displaystyle a}$

Using these unit vectors, the coordinates of the sun and moon can now be determined in this coordinate system. Due to the definition of the fundamental plane, the and coordinates of the sun and moon are identical. These simultaneously represent the intersection of the shadow axis with the fundamental plane and are the next determined Bessel elements. Furthermore, the coordinate of the moon is determined, as this is required for the calculation of the shadow radii. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$

${\displaystyle x=\mathbf {r} _{m}\cdot \mathbf {i} =r_{m}\cos \delta _{m}\sin \left(\alpha _{m}-a\right)}$

${\displaystyle y=\mathbf {r} _{m}\cdot \mathbf {j} =r_{m}\left(\sin \delta _{m}\cos d-\cos \delta _{m}\sin d\cos \left(\alpha _{m}-a\right)\right)}$

${\displaystyle z_{m}=\mathbf {r} _{m}\cdot \mathbf {k} =r_{m}\left(\sin \delta _{m}\sin d+\cos \delta _{m}\cos d\cos \left(\alpha _{m}-a\right)\right)}$

Determination of the cone angles for penumbra and umbra ( and ); For the sake of clarity, only one tangent is shown in each case ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$

The angles between the shadow axis and the tangents to the sun and moon, which form the cone coats of the penumbra and umbra, can be determined using an auxiliary triangle. The tangents are shifted parallel so that they go through the center of the moon (see figure on the right). The hypotenuse of both triangles is the line connecting the center of the sun and the moon, the opposite cathetuses of the angles sought form the lines through the center of the sun at right angles on the parallel shifted tangents. In these right-angled triangles, the length of two sides is known, on the one hand the distance between the sun and the moon, and on the other hand the length of the opposite cathetus, which corresponds to the sum of the sun and moon radius in the case of the penumbra and the difference between these two sizes in the case of the umbra. Thus:

${\displaystyle \sin f_{1}={\frac {\rho _{s}+\rho _{m}}{|\mathbf {r} _{s}-\mathbf {r} _{m}|}}}$

${\displaystyle \sin f_{2}={\frac {\rho _{s}-\rho _{m}}{|\mathbf {r} _{s}-\mathbf {r} _{m}|}}}$

In order to calculate the last two missing Bessel elements and , the radii of penumbra and umbra in the fundamental plane, the distance between the intersection of the tangents and the shadow axis from the fundamental plane is required. For the penumbra, this point marked with is on the shadow axis between the sun and moon and represents the tip of the penumbra cone. The point of intersection is also on the shadow axis and is the tip - that is, the end point - of the umbra. The following applies: ${\displaystyle l_{1}}$ ${\displaystyle l_{2}}$ ${\displaystyle V_{1}}$ ${\displaystyle V_{2}}$

${\displaystyle z_{V_{1}}=z_{m}+{\frac {\rho _{m}}{\sin f_{1}}}}$

${\displaystyle z_{V_{2}}=z_{m}-{\frac {\rho _{m}}{\sin f_{2}}}}$

Using these distances between the points and the fundamental plane, the radii of the shadow cones in this plane can be determined as follows: ${\displaystyle V_{1}}$ ${\displaystyle V_{2}}$

${\displaystyle l_{1}=z_{V_{1}}\tan f_{1}}$

${\displaystyle l_{2}=z_{V_{2}}\tan f_{2}}$

If the cone tip of the umbra falls behind the fundamental plane as seen from the moon, i.e. if there is a total solar eclipse, it is negative, in the other case positive, which is the case with an annular solar eclipse. In accordance with the convention, the sign of the umbra radius is chosen so that it is given negative in the case of total visibility, but positive in the case of circular visibility. The sizes and are always positive. ${\displaystyle z_{V_{2}}}$ ${\displaystyle l_{2}}$ ${\displaystyle z_{V_{1}}}$ ${\displaystyle l_{1}}$

A moon radius is selected for the calculation, which represents an averaging of the irregularities of the moon's edge ( ). However, since the totality of an eclipse does not exist as long as sun rays shining through the deepest lunar valley still reach the observation site, a second, smaller value ( ) is used to calculate the totality zone and duration . ${\displaystyle \rho _{m}=0{,}2725076}$ ${\displaystyle \rho _{m}=0{,}272281}$

Publication of the Bessel elements

The Bessel elements are time-dependent. In order to describe an eclipse, they must therefore be specified for a period of time that, for example, includes several hours to fully describe a solar eclipse.

There are different versions of the publication of the Bessel elements of a solar eclipse. In some cases, the values are not all (so as to be regarded constant elements , , , , and ) given in hourly intervals for the entire course of Darkness table. Intermediate values can be interpolated . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle d}$ ${\displaystyle \mu }$ ${\displaystyle l_{1}}$ ${\displaystyle l_{2}}$

Another variant is to specify the Bessel elements for a reference time ( ), for example the full hour closest to the maximum in terrestrial time (TT), and also the hourly changes for all elements that are not considered constant. This enables the calculation of the values ​​for other points in time of the course of the eclipse as a linear function of time. ${\displaystyle t_{0}}$

The specification in polynomial form enables a somewhat more precise approximation compared to linear interpolation. In addition to the value at the time, up to three polynomial coefficients are specified for the variable quantities . The calculation of the value at a certain time is then carried out in the following form: ${\displaystyle t_{0}}$

${\displaystyle \sum _{n=0}^{n_{\mathrm {max} }}a_{n}t^{n}}$

One of the variable quantities corresponds to the difference to the time in hours. ${\displaystyle a}$ ${\displaystyle t}$ ${\displaystyle t_{0}}$

In practice, often by the Goddard Space Flight Center of NASA resorted elements published in polynomial form Bessel. Measures taken in the Astronomical Almanac published Bessel elements of the value is for practical reasons already using the candidate trigonometric functions ( sine and cosine specified), also the sizes , which can be regarded for the entire eclipse course approximately as a constant hourly changes in the sizes and . ${\displaystyle d}$ ${\displaystyle d'}$ ${\displaystyle \mu '}$ ${\displaystyle \mu }$ ${\displaystyle d}$

Example of the application of the Bessel elements

In the following example, the Bessel elements are calculated for a given point in time, so that the position and size of the umbra and penumbra cone in the fundamental plane are known at this point in time. For practical applications it must then be investigated how points on the earth's surface lie relative to these shadow cones. All sizes required for this are given by the geometry of the earth. The example examines whether a given location lies within the umbra cone.

Determination of the Bessel elements for a specific point in time

Bessel elements (polynomial coefficients)
reference time = August 11, 1999 11:00:00 dd ${\displaystyle t_{0}}$

${\displaystyle n}$	${\displaystyle x}$	${\displaystyle y}$	${\displaystyle d}$	${\displaystyle l_{1}}$	${\displaystyle l_{2}}$	${\displaystyle \mu }$
0	0.0700420	0.5028410	15.327340	0.5424690	−0.0036500	343,687410
1	0.5443035	−0.1184929	−0.012035	0.0001168	0.0001163	15.002982
2	−0.0000406	−0.0001158	−0.000003	−0.0000117	−0.0000116
3	−0.0000081	0.0000017
${\displaystyle \tan f_{1}}$= 0.0046129;       = 0.0045900 ${\displaystyle \tan f_{2}}$

The adjacent table contains the Bessel elements of the solar eclipse of August 11, 1999 in polynomial form. The goal is now to calculate the position of the umbra in the fundamental plane for 12:34:03  CEST (corresponds to 10:34:03 UT).

First of all the difference to the reference time (11:00:00:00 DD ) must be determined. The difference between TT and Universal Time (UT) must be taken into account, which was 63.7 seconds at the time of the eclipse: ${\displaystyle \Delta T}$

${\displaystyle t=10{,}5675-11{,}0+{\frac {63{,}7}{3600}}=-0{,}414805556}$

The coordinates of the intersection of the shadow axis with the fundamental plane for the desired time are calculated as follows:

${\displaystyle x=0{,}070042+0{,}5443035\ t-0{,}0000406\ t^{2}-0{,}0000081\ t^{3}=-0{,}155744523}$

${\displaystyle y=0{,}502841-0{,}1184929\ t-0{,}0001158\ t^{2}+0{,}0000017\ t^{3}=0{,}551972467}$

The declination and hour angle are calculated in the same way (the values ​​for or that are missing in the table must be set to 0): ${\displaystyle n=2}$ ${\displaystyle n=3}$

${\displaystyle d=15{,}32734-0{,}012035\ t-0{,}000003\ t^{2}=15{,}33233167}$

${\displaystyle \mu =343{,}687410+15{,}002982\ t=337{,}4640897}$

The radius of the umbra in the fundamental plane can now also be calculated for this point in time:

${\displaystyle l_{2}=-0{,}0036500+0{,}0001163\ t-0{,}0000116\ t^{2}=-0{,}003700238}$

The penumbra radius can be calculated in the same way, but it is not required for the following calculation.

Check whether a given point is in the totality zone at this time

In the first step, the Bessel elements of the eclipse of August 11, 1999 were calculated for 12:34:03 CEST. Now it should be checked whether the Stuttgart Schloßplatz ( 48 ° 46 '42.8 "  N , 9 ° 10' 47.7"  E ) was in the totality zone at this point in time. For this purpose, the coordinates of the castle square are converted into the fundamental coordinate system. Once these coordinates have been determined, it can easily be determined whether this point lies within the shadow cone, since the shadow axis is, by definition, perpendicular to the fundamental plane.

First of all, the given geodetic coordinates of the castle square ( = 48.77855 ° and = 9.17991 °) including the ellipsoidal height ( = 295 m) are to be converted into geocentric spherical coordinates ( and ), with the length remaining unchanged. For this purpose, the numerical eccentricity of the Earth's ellipsoid of revolution and two other latitude-dependent auxiliary variables derived from it are used: ${\displaystyle \phi }$ ${\displaystyle \lambda }$ ${\displaystyle h}$ ${\displaystyle \phi '}$ ${\displaystyle \rho }$ ${\displaystyle \lambda }$ ${\displaystyle e}$

Relationship between geodetic latitude and geocentric latitude ${\displaystyle \phi }$ ${\displaystyle \phi '}$

${\displaystyle e^{2}=1-{\frac {b^{2}}{a^{2}}}=0{,}006694380}$

Here is the equatorial radius and the polar radius. ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle C={\frac {1}{\sqrt {1-e^{2}\sin ^{2}\phi }}}=1{,}001899093}$

${\displaystyle S=\left(1-e^{2}\right)C=0{,}995191999}$

With the equator radius = 6,378,137 m, the geocentric coordinates can be calculated as follows: ${\displaystyle a}$

${\displaystyle \phi ^{\prime }=\arctan {\frac {\left(aS+h\right)\tan \phi }{aC+h}}=48{,}5877227^{\circ }}$

${\displaystyle \rho ={\frac {\left(aC+h\right)\cos \phi }{a\cos \phi ^{\prime }}}=0{,}998156295}$

It expresses the distance of the Schloßplatz from the center of the earth in units of the equatorial radius, is the angle between the equatorial plane and the position vector pointing from the center of the earth to the Schloßplatz . ${\displaystyle \rho }$ ${\displaystyle \phi '}$

Geocentric angle in the equatorial plane: is the right ascension of the shadow axis, the longitude of the observer, the sidereal time related to Greenwich , the hour angle of the shadow axis (already corrected by) and the hour angle of the observer to the shadow axis ${\displaystyle a}$ ${\displaystyle \lambda }$ ${\displaystyle \theta _{0}}$ ${\displaystyle \mu }$ ${\displaystyle \Delta T}$ ${\displaystyle \theta }$

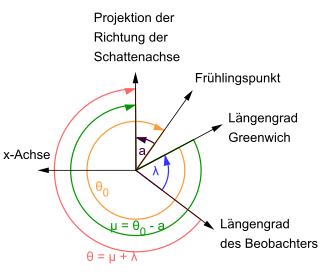
The hourly angle of the observation location relative to the axis of the fundamental coordinate system is now determined as an auxiliary variable . It should be noted that with the Bessel elements, the hour angle is calculated assuming an ephemeris day (corresponding to terrestrial time, previously: ephemeris time). However, since the actual rotation of the earth is not quite regular, the time difference between terrestrial time and universal time must first be corrected, which corresponds. The sidereal day length is decisive for calculating the corresponding angular correction ; the difference to the synodic day length ( sunny day ) is taken into account by the factor 1.002738. Actually, the geographical longitude of the observer ( ) has to be subtracted from, but since both angles are measured in opposite directions, it is an addition. ${\displaystyle \theta }$ ${\displaystyle z}$ ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle \Delta T}$ ${\displaystyle \lambda }$ ${\displaystyle \mu }$

${\displaystyle \theta =\left(\mu -1{,}002738\cdot {\frac {360^{\circ }}{86400\mathrm {s} }}\Delta T\right)+\lambda =346{,}3778563^{\circ }}$

Thus, let the Cartesian coordinates , and the Castle Square in the fundamental coordinate system as determined, following the inclination of the fundamental plane with respect to the geodetic coordinate system by the declination is taken into account: ${\displaystyle \xi }$ ${\displaystyle \eta }$ ${\displaystyle \zeta }$ ${\displaystyle d}$

${\displaystyle \xi =\rho \cos \phi ^{\prime }\sin \theta =-0{,}155501299}$

${\displaystyle \eta =\rho \sin \phi ^{\prime }\cos d-\rho \cos \phi ^{\prime }\sin d\cos \theta =0{,}552271870}$

${\displaystyle \zeta =\rho \sin \phi ^{\prime }\sin d+\rho \cos \phi ^{\prime }\cos d\cos \theta =0{,}816780948}$

The radius of the intersection of the umbra cone in the plane running through the castle square, parallel to the fundamental plane, is closer to the sun and moon and is therefore somewhat larger than the umbra radius in the fundamental plane. It can be calculated on the basis of the cone angle of the shadow cone ( ) given in the Bessel elements and the distance between the castle square and the fundamental plane ( ). It should be noted that the umbra radius is given negative by definition in a total eclipse. ${\displaystyle \tan f_{2}}$ ${\displaystyle \zeta }$

${\displaystyle l_{2,\zeta }=l_{2}-\zeta \ \tan f_{2}=-0{,}007449262}$

The distance between the castle square and the shadow axis in the same plane can be determined as follows: ${\displaystyle r}$

${\displaystyle r={\sqrt {\left(\xi -x\right)^{2}+\left(\eta -y\right)^{2}}}=0{,}000385746<0{,}007449262}$

Since the distance between the castle square in this level is smaller than the radius of the shadow cone, the castle square was therefore within the core shadow at the given time. Because it was raining in Stuttgart at that time, however, it was not possible to observe the darkened sun on the Schlossplatz.

By performing these calculations iteratively for a period of time, the contact times at a specific location can in principle be determined. However, there are also direct methods of calculating contact times.

Further celestial coverings by the moon

Star occultations by the moon

Shadow cylinder with a star occlusion

In the case of star occultations, the calculation of the Bessel elements can be greatly simplified compared to solar eclipses, since it is sufficiently accurate to regard the covered celestial body as infinitely far away. This assumption makes it possible to consider the rays of light from the distant object reaching the Earth-Moon system to be parallel. This means that the direction of the shadow axis, i.e. the axis of Bessel's fundamental coordinate system, always points exactly in the direction of the star during the entire course of the eclipse and is therefore given from the outset by the equatorial coordinates of the star. ${\displaystyle z}$

Another simplification compared to a solar eclipse is that no umbra and penumbra cone have to be described, but that it is sufficient to understand the "shadow" as a cylinder that is perpendicular to the fundamental plane . The radius of this cylinder is equal to the radius of the moon, which is 0.2725 of the earth's equatorial radius. There is no need to specify variable shadow radii or opening angles.

The fundamental plane is chosen analogously to the solar eclipses, i.e. the normal plane of this shadow axis that goes through the center of the earth. The line of intersection of the fundamental plane with the equatorial plane is the -axis and points to the east, perpendicular to this in the center of the earth is the -axis and points to the north. As with solar eclipses, all information in this coordinate system is given in units of the equatorial radius. ${\displaystyle x}$ ${\displaystyle y}$

In contrast to the solar eclipse, the reference time for the Bessel elements is often not a full hour, but the time of the conjunction in right ascension , i.e. the time at which the star and moon have the same right ascension . At this point in time, the coordinate of the cylinder axis has the value 0, so that only the coordinate of the cylinder axis in the fundamental plane is specified in tables . The Bessel elements of a star eclipse are then determined as follows: ${\displaystyle T_{0}}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle \!\ T_{0}}$	The time of the conjunction in right ascension , given in Universal Time (UT)
${\displaystyle \!\ H}$	The hour angle of the star at the time ${\displaystyle T_{0}}$
${\displaystyle \!\ Y}$	The value for at the time ${\displaystyle y}$ ${\displaystyle T_{0}}$
${\displaystyle \!\ x',y'}$	The change in time from and per hour ${\displaystyle x}$ ${\displaystyle y}$
${\displaystyle \!\ \alpha ,\delta }$	Right ascension and declination of the star ( star location ) and at the same time the direction of the -axis ${\displaystyle z}$

For forecasting calculations it is sufficient, and to be regarded as constant during the entire course of the coverage. ${\displaystyle x'}$ ${\displaystyle y'}$

The planets are covered by the moon

The method of the Bessel elements can be applied to any celestial cover if both celestial bodies are sufficiently exactly spherical. You only have to replace the position and size of the sun with that of the planet in question. As an exception, Bessel only gave the planets Jupiter and Saturn in 1842 , since their deviation from the spherical shape was measurable at that time. To predict the area of ​​visibility for occultations of planets by the moon, the same simplified procedure can be used as for star occultations (see above ).

However, if the contact times are to be determined precisely, any deviations of the planet from the spherical shape must be taken into account, as well as which part of the planetary disk is illuminated by the sun at the time it is covered. This method was described by Chauvenet in 1865 because Bessel's method was no longer accurate enough for the observation methods that had become more precise in the meantime. The part of the planet that is illuminated by the sun and visible from the earth is viewed directly and not mapped onto a fundamental plane.

Transit of the lower planets

During the transit of the lower planets Venus and Mercury in front of the sun, the covering celestial body is the planet. This can never completely cover the sun, because the umbra is far too short to fall on earth. Bessel elements are also used for these astronomical events to calculate the local conditions. Exactly the same calculation method can be used as for solar eclipses, with the planet taking on the role of the moon.

Since the distance of the lower planets from the earth is much greater than that of the moon, there is the possibility of a simplified calculation of the times of entry and exit of the planetary disc in front of the sun during transits. This method works without converting the ephemeris into Bessel's fundamental coordinate system. Use is made use of the fact that the squared or higher potency raised parallax of the planet is so small that it can be ignored. Based on the contact times related to the center of the earth, the corresponding points in time can be calculated in this way at every point on the earth. The principle of this simplified calculation goes back to Lagrange and was improved by William Chauvenet by taking into account the flattening of the earth.

Lunar eclipses

During a lunar eclipse there is an earthly observer on the celestial body, which casts the shadow. Thus, one sees exactly the same eclipse course from all places on earth, provided the moon is visible. When calculating lunar eclipses, corresponding viewing angles ( polar coordinates ) are determined, which is similar to the determination of the Bessel elements ( Cartesian coordinates in the Bessel fundamental plane). That is why the viewing angles used for lunar eclipses are sometimes also called Bessel elements. However, a fundamental plane is neither used for the earth nor for the moon, and the description of lunar eclipses is usually exclusively polar coordinates.

As with solar eclipses, the fundamental coordinate system relates to the shadow axis, which in lunar eclipses always goes through the center of the earth. The calculation is similar to that for solar eclipses. In this case, the right ascension and declination of the shadow axis result directly from the corresponding values ​​of the sun, but the -axis points away from the sun. Thus: ${\displaystyle z}$

${\displaystyle a=\alpha _{s}+180^{\circ };\quad \quad d=-\delta _{s}}$

In the same way as with solar eclipses, the geocentric position vector of the moon can be converted into the fundamental system. The position of the center of the moon in relation to the shadow axis can be determined via its and components. Since all angles used have their apex in the center of the earth, in contrast to solar eclipses, no length information is required for the conversion. The coordinates and relate to the unit sphere . The angles derived from this are given in arc seconds . Except for the missing unit conversion, the formulas used correspond to those used for the solar eclipse. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle x=\cos \delta _{m}\sin \left(\alpha _{m}-a\right)}$

${\displaystyle y=\sin \delta _{m}\cos d-\cos \delta _{m}\sin d\cos \left(\alpha _{m}-a\right)}$

From this the angular distance between the center of the moon and the shadow axis can be calculated:

${\displaystyle m={\sqrt {x^{2}+y^{2}}}}$

Geometry of the umbra of a lunar eclipse

The size of the radii of penumbra and umbra are also given as geocentric viewing angles. The sizes and describe the viewing angle of the shadow radii in the lunar orbit. In the illustration opposite, the dashed line indicates the orbit of the moon. The angle is the viewing angle of the earth's radius as seen from the moon and thus corresponds to the parallax of the moon. Since this angle is an outer angle of the triangle , applies to the viewing angle of the umbra in the lunar orbit ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$ ${\displaystyle \pi _{m}}$ ${\displaystyle \Delta EM'V_{2}}$ ${\displaystyle f_{2}}$

${\displaystyle f_{2}=\pi _{m}-v_{2}\!\,}$,

where is half the opening angle of the umbra cone. Analogously, another angle relationship can be derived from the triangle : The outer angle corresponds to the viewing angle of the sun's radius from the earth, the angle to the geocentric parallax of the sun. Thus: ${\displaystyle v_{2}}$ ${\displaystyle \Delta ES'V_{2}}$ ${\displaystyle r_{s}}$ ${\displaystyle \pi _{s}}$

${\displaystyle v_{2}=r_{s}-\pi _{s}\!\,}$

The desired angle can now be determined from both angle relationships by eliminating the cone angle: ${\displaystyle v_{2}}$

${\displaystyle f_{2}=\pi _{s}+\pi _{m}-r_{s}\!\,}$

The geocentric viewing angle of the penumbra radius in the lunar orbit can also be determined in an analogous manner. The following relationship results for this:

${\displaystyle f_{1}=\pi _{s}+\pi _{m}+r_{s}\!\,}$

Bessel elements for the contact times of a lunar eclipse

In order to support the determination of the contact times of the eclipse, three additional auxiliary variables are derived from the sizes of the umbra and penumbra and the moon radius. These are the viewing angles for the distance of the center of the moon from the shadow axis during a given contact, which are calculated from the viewing angles of the shadow radii and the viewing angle of the moon radius: ${\displaystyle r_{m}}$

${\displaystyle L_{1}=f_{1}+r_{m}\!\,;}$ Entry and exit of the moon for the penumbra

${\displaystyle L_{2}=f_{2}+r_{m}\!\,;}$ Entry and exit of the moon for the umbra

${\displaystyle L_{3}=f_{2}-r_{m}\!\,;}$ Beginning and end of total darkness

The sizes , , , , , , and , and , and - the hourly rates of change for the corresponding sizes - are considered Bessel elements of a lunar eclipse. They are given for a reference time, for example the time of the moon opposition . In contrast to solar eclipses, however, there is no generally recognized way of specifying the parameters. ${\displaystyle x\!\,}$ ${\displaystyle y\!\,}$ ${\displaystyle m\!\,}$ ${\displaystyle L_{1}\!\,}$ ${\displaystyle L_{2}\!\,}$ ${\displaystyle L_{3}\!\,}$ ${\displaystyle f_{1}\!\,}$ ${\displaystyle f_{2}\!\,}$ ${\displaystyle {\dot {x}}}$ ${\displaystyle {\dot {y}}}$ ${\displaystyle {\dot {m}}}$

The calculations presented so far only used angles to the shadow axis and managed without a definition of the fundamental plane. If you want to calculate when certain lunar craters - i.e. distinctive points on the lunar surface - enter or exit the umbra, this is possible if you choose the fundamental plane so that it goes through the center of the moon - in a similar way to points on the earth's surface at Solar eclipses.

When checking the calculated contact times and, in particular, the entry and exit times of certain moon craters into and out of the umbra, the data calculated in this way do not show any useful correspondence with reality. On the one hand, this is due to the fact that the earth does not cast a sufficiently circular shadow due to its flattening . Second, it is due to the earth's atmosphere , which enlarges the shadow cones. To compensate for these effects, it is common to introduce two correction factors into the formulas for calculating the size of the penumbra and umbra cone, where the factor 1.02 is the enlargement of the earth's shadow by the effect of the earth's atmosphere by 1/50 and the factor 0, 998340 is intended to compensate for the flattening of the earth in the mean value between the equator and pole diameter:

${\displaystyle f_{1}=1{,}02\left(0{,}998340\ \pi _{m}+\pi _{s}+r_{s}\right)}$

${\displaystyle f_{2}=1{,}02\left(0{,}998340\ \pi _{m}+\pi _{s}-r_{s}\right)}$

André Danjon pointed out in 1951 that in order to take into account the effect of the earth's atmosphere, the two shadow cones should not be enlarged by the same relative amount of 1/50, but rather an enlargement by the same absolute amount corresponds to the actual geometric relationships. Danjon assumes a 75-kilometer-high layer of the earth's atmosphere, which has an absorbing effect, which corresponds to an increase in the earth's radius or the parallax of the moon by 1/85. The factor 1.01 combines this magnification with the factor for the earth flattening:

${\displaystyle f_{1}=1{,}01\ \pi _{m}+\pi _{s}+r_{s}}$

${\displaystyle f_{2}=1{,}01\ \pi _{m}+\pi _{s}-r_{s}}$

Eclipse sizes for umbra eclipses, which are calculated according to the 1/50 rule, are around 0.005 too large compared to the calculation according to Danjon, for penumbral eclipses around 0.026.

But even data calculated in this way do not yet show a particularly precise correspondence with reality. This is mainly attributed to the fact that the flattening of the earth's atmosphere is still significantly larger than that of the earth's surface. An attempt is being made to develop a more precise correction method based on the observation data of various lunar eclipses.

Remarks

1. ↑ Typically , ephemeris (DE200 / LE200) published by the Jet Propulsion Laboratory are used as the basis. These ephemeris refer to the centers of mass of the heavenly bodies. For eclipses, however, the center of the lunar, planetary or solar disk is decisive. This has a disruptive effect in the case of the moon, whose center of mass is about two kilometers closer to the earth than its geometric center. The size of the deviation caused thereby shows a connection to the libration . If such corrections to the coordinates of the moon were made during the calculation of Bessel's elements, this is indicated ( and ). ${\displaystyle \Delta \beta }$ ${\displaystyle \Delta \lambda }$
2. ↑ The ellipsoidal height for Stuttgart is about 49 m higher than the NHN or NN height.
3. ↑ Please note that this correction of can already be included in the tabulated representation of the Bessel elements, such as in the Astronomical Almanac . ${\displaystyle \mu }$
4. ↑ Danjon uses a value of 1/297 for the flattening of the earth; the mean value between the equator and earth diameter is 0.5 x 1/297 = 1/594 to correct the size of the shadow. This results in the shadow magnification of 1 + 1/85 - 1/594 ~ 1.01.

literature

• P. Kenneth Seidelmann (Ed.): Explanatory Supplement to the Astronomical Almanac. University Science Books, Sausalito 2006, ISBN 1-891389-45-9
• Robin M. Green: Spherical astronomy. Cambridge University Press, Cambridge 1985, ISBN 0-521-23988-5
• William Chauvenet: A manual of spherical and practical astronomy. JB Lippincott & Co, Philadelphia 1863, books.google.de
• Jean Meeus : Elements of Solar Eclipses 1951-2200. Willmann-Bell, Richmond 1989, ISBN 0-943396-21-2 (With calculation method and the Bessel elements of all solar fins between 1951 and 2200.)
• Jean Meeus: Transits. Willmann-Bell, Richmond 1989, ISBN 0-943396-25-5 (With calculation method and the Bessel elements of all Mercury transits in the period 1600 to 2300 and all Venus transits -2000 to 4000.)
• Jean Meeus: Astronomical Tables of the Sun, Moon and Planets 3rd edition. Willmann-Bell, Richmond 20015, ISBN 978-1-942675-03-7 (With calculation method and the Bessel elements for occultations of bright stars in the period 2010 to 2040.)

Individual evidence

1. ↑ ^{a b c d e f} Hermann Mucke , Jean Meeus : Canon of solar eclipses: -2003 to +2526. Astronomisches Büro, Vienna 1992, page XXXIII – LI
2. ↑ ^{a b c d e} Michael Altmann: Course of brightness during solar eclipses (II) (PDF; 71 kB)
3. ↑ Friedrich Wilhelm Bessel: Calculation of different star coverages by Messrs. Rosenberger, Strehlke and Klupsz. In: Astronomische Nachrichten , No. 50, 3, February 1824, pp. 17–28, bibcode : 1824AN ...... 3 ... 17R (full text available)
4. ↑ Friedrich Wilhelm Bessel: About the advance calculation of the star coverages. In: Astronomische Nachrichten , No. 145, 7, September 1828, pp. 1–16, bibcode : 1828AN ...... 7 .... 1B (full text available)
5. ↑ ^{a b} Friedrich Wilhelm Bessel: Contributions to the theory of eclipses and the calculation methods of the same. In: Astronomische Nachrichten , No. 151, 7, January 1829, pp. 121-136, bibcode : 1829AN ...... 7..119. (Full text available)
6. ^ Friedrich Wilhelm Bessel: Contributions to the theory of eclipses and the calculation methods of the same (decision). In: Astronomische Nachrichten , No. 152, 7, February 1829, pp. 137–144, bibcode : 1829AN ...... 7..137B (full text available)
7. ^ ^{A b} Friedrich Wilhelm Bessel: Astronomical investigations. Volume 2, Königsberg 1842 ( books.google.de )
8. ^ Roberdeau Buchanan: The Mathematical Theory of Eclipses According to Chauvenet's Transformation of Bessel's Method. P. 17 f., Philadelphia / London 1904
9. ↑ Fred Espeneak: Besselian Elements of Solar Eclipses . NASA
10. ↑ ^{a b c d} Robin M. Green: Spherical astronomy. P. 459 ff., See literature
11. ^ P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac. P. 424 f., See literature
12. ^ ^{A b} P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac. Pp. 435-441, see literature
13. ↑ ^{a b c d e f g} Robin M. Green: Spherical astronomy. Pp. 450-453, see literature
14. ↑ Otto Praxl solar and lunar eclipses.
15. ↑ Fred Espenak, Jay Anderson: Total Solar Eclipse of 2008 August 01. (PDF; 7.8 MB) March 2007, p. 6
16. ^ Jean Meeus, Carl Grosjean, Willy Vanderleen: Canon of Solar Eclipses. Pergamon Press, Oxford, 1966
17. ^ NASA Eclipse website
18. ↑ Astronomical Almanac 2005. S. A78ff., Stationery Office Books, 2003 ( books.google.de )
19. ↑ Fred Espeneak (NASA): Besselian Elements for the Total Solar Eclipse of 1999 Aug 11
20. ^ ^{A b} P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac. Pages 441–446, see literature
21. ↑ Shy Sofi - the solar eclipse in Stuttgart . ( Memento of the original from July 3, 2010 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. von-zeit-zu-zeit.de 
22. ^ ^{A b c} P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac. Pages 494–497, see literature
23. ^ William Chauvenet: A manual of spherical and practical astronomy. P. 565, see literature
24. ^ Jean Meeus: Transits. Willmann-Bell, 1989, ISBN 0-943396-26-3
25. ^ ^{A b} William Chauvenet: A manual of spherical and practical astronomy. Pp. 593-598, see literature
26. ^ P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac. P. 471, see literature
27. ↑ ^{a b c d e f} P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac. Page 467-470.
28. ^ ^{A b} Robin M. Green: Spherical astronomy. Page 441f, see literature
29. ^ P. Kenneth Seidelmann: Explanatory Supplement to the Astronomical Almanac. Pages 428–431, see literature
30. ↑ A. Danjon: Les Eclipses de Lune par la pénombre en 1951. In: L'Astronomie , 65, p. 51-53
31. ^ J. Meeus, H. Mucke: Canon of Lunar Eclipses -2002 to +2526 , page XXIV
32. ^ Byron W. Soulsby: Improved lunar eclipse ephemerides. In: Journal of the British Astronomical Association. , 100, 1990, pp. 293–305, bibcode : 1990JBAA..100..293S (full text available / PDF; 2.0 MB)

This article was added to the list of excellent articles on December 8, 2010 in this version .