Sidereal time

The sidereal time is in the astronomy used time scale and is based on the apparent motion of the star as a result of the rotation of the earth. A sidereal day is the length of time that the starry sky (more precisely: the spring equinox ) needs for an entire apparent orbit around the earth. Compared to the usually used solar time , which is based on the apparent orbit of the earth by the sun, the sidereal day is almost four minutes shorter than the solar day .

Like the sunny day, the sidereal day is divided into 24 but shorter hours. It begins when the vernal equinox passes the meridian of the observation site and ends there with its next passage. The observer - usually an astronomer in an observatory - draws conclusions from the sidereal time about the momentary view of the sky. The sidereal time is derived from the right ascension angle - a primary quantity for the position of the stars in the sky. For example, a star with a 15 ° difference in right ascension to the vernal equinox passes the meridian one sidereal hour later than the latter. This fact can be briefly stated that it is, for example, 1:00 a.m. sidereal time. It should be noted, however, that sidereal time is a time that is tied to the location. To make it easier to compare the time for observations made at different locations, the local sidereal time clocks are set to the sidereal time of Greenwich. The time difference is - as with the solar time - 1 hour for a 15 ° difference in length between the observation locations.

Observing work using sidereal time has the advantage that at the same sidereal time the stars are always in the same direction in the sky. Compared to the normal clock, the sidereal time clock advances by about 4 more minutes every day. After a year it overtakes the latter and briefly agrees with it again.

The general time determination according to Universal Time (UT) (a solar time) is carried out in practice by the more exact possible observation of the star positions. The sidereal time determined in this way is converted into the associated UT using a formula established by convention (see below).

Definition and characteristics

Sidereal time is defined as the hour angle of the vernal equinox . If you refer to the mean spring equinox , you get the mean sidereal time . If you refer to the true vernal equinox , you get the apparent or true sidereal time .

The cause of the continuous increase in the mentioned hour angle is the earth's rotation . The sidereal time is thus subject to all short-term and long-term irregularities of the earth's rotation and is therefore not a uniform measure of time. But it is always a true reflection of the rotation angle of the earth with respect to the vernal equinox.

Since the vernal equinox moves due to precession with respect to the fixed star background, a sidereal day (i.e. one full revolution of the earth with respect to the vernal equinox) is slightly shorter than one earth rotation (i.e. one full revolution of the earth with respect to the fixed star background). Since the vernal equinox moves retrograde by about 0.137 arcseconds along the ecliptic, a mean sidereal day is 0.009 seconds shorter than an earth's rotation.

The true vernal equinox differs from the middle vernal equinox by the mutation itself . The apparent sidereal time is therefore subject to an additional irregularity compared to the (itself already non-uniform) mean sidereal time, the main component of which fluctuates with a period of 18.6 years and an amplitude of ± 1.05 seconds.

The vernal equinox hour angle is the same for observers on the same longitude, but different for observers on different longitudes. The sidereal time derived from this is therefore a local time. The sidereal time of the reference location Greenwich is the Greenwich sidereal time. It is required particularly often in calculations. The different types of sidereal time are often referred to by their English abbreviations:

LAST: local apparent sidereal time, apparent local sidereal time
LMST: local mean sidereal time, local mean sidereal time
GUEST: Greenwich apparent sidereal time, apparent Greenwich sidereal time
GMST: Greenwich mean sidereal time, central Greenwich sidereal

The hour angle of the vernal equinox is the angle counted along the celestial equator from the meridian to the vernal equinox. A star's right ascension, on the other hand, is the angle from the vernal equator to the star, counted along the celestial equator. If the star is on the meridian (that is, if the star culminates ), both angles are equal. It follows from this: At the moment of the culmination of a star, the sidereal time is equal to the right ascension of the star.

Sidereal time is the right ascension in the upper culmination.

This can be used to directly determine the right ascension of the star by observing the time of culmination. That is the reason why the right ascension is often given in time units instead of in angular units: it is then immediately the sidereal time read at the time of culmination. Wega, for example, has a right ascension of 18 ^h 36 ^m 56 ^s , so it will always culminate at 18 ^h 36 ^m 56 ^s local sidereal time.

On the other hand, the current sidereal time can be determined by observing the culmination of a star with a known right ascension: When Wega culminates, the sidereal time is 18 ^h 36 ^m 56 ^s (in practice, corrections for precession, proper motion , parallax , etc.)

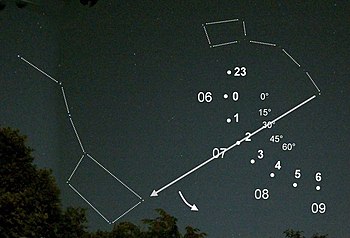
1. The “star hour hand” rotates on a dial fixed on the horizon:
after a 15 ° turn (scale 0 °, 15 °, 30 °, ...) a sidereal hour (scale 23, 0, 1, ...) has passed .
2. The “star hour hand” rotates on a dial that is dragged along by the sun and rotates around the North Star:
after about a month (scale 06, 07, 08, ...) it is 30 ° in relation to the sun (scale 0 °, 15 °, 30 °, ...) ran ahead.

Rotation of the star sky

Daily rotation

The starry sky can be imagined as a large clock disk that rotates counterclockwise (in the northern hemisphere) on a sidereal day. In the picture, this disk is marked with a pointer between the Pole Star and the Big Bear . The 24-hour dial (scale 23, 0, 1, ...) is fixed on the horizon. If the pointer has rotated 15 ° further (scale 0 °, 15 °, 30 °, ...), one sidereal hour has passed. For one hour of solar time it has to turn slightly further.

Annual rotation

On a dial that is dragged along by the sun and revolves around the North Star, one observes a very slow advance of the pointer. The pointer circles it once a year: 30 ° (scale 0 °, 15 °, 30 °, ...) in about a month (scale 06, 07, 08, ...).

The picture was taken at the beginning of July (number 07) around 2:00 a.m. Two hours later (around 4:00 a.m.), the Big Dipper moved on to number 4. A month later in August (number 08) it is already at number 4 at 2:00 a.m.

Sidereal day and sunny day

Sidereal day (1 to 2) and
solar day (1 to 3),
(The slope of the earth's axis on the earth's orbit has been neglected here.)

The solar day as the basis of the generally used solar time lasts slightly longer than the sidereal day because the sun moves around the earth - also apparently - slightly more slowly than the stars. The reason for this is again the own movement of the earth, namely its annual orbit around the sun.

The sidereal day is about 1/365 (length of the year is 365.2422 days) shorter than the solar day. Measured on the 24 hours of the solar day, the sidereal day is 23 hours, 56 minutes and 4.091 seconds long. The sidereal day is itself divided into 24 hours, its hours into 60 minutes and its minutes into 60 seconds.

Due to the nutation of the earth, the vernal equinox fluctuates with a period of about 18.6 years. Accordingly, a distinction is made between the true sidereal time , which results from direct observation, and the mean sidereal time , which is freed from these fluctuations. The difference between true and mean sidereal time is a maximum of about 1.1 seconds.

Sidereal time and stargazing

Knowing the sidereal time makes observing the stars much easier. In observatories one uses clocks that show the sidereal time. They go in sync with the stars running in the sky. At a fixed location , every star passage through a certain altitude or direction has a fixed sidereal time and can therefore be entered immovably in an observation schedule according to sidereal time. It should be noted that the possible nocturnal observation time runs through the timetable once a year.

Like True Solar Time, sidereal time is a local time. Just as with the true solar time it is 12 o'clock (noon), when the sun passes through the local meridian , with sidereal time it is 0 o'clock when the spring point is in the local meridian. Unifying the sidereal time to one zone time would be absurd. On the contrary: The sidereal time contained in yearbooks for a day applies to a certain degree of longitude. It must be converted to the longitude of the observation site in order to be able to work with it profitably (+ 4 minutes sidereal time per degree to the west).

From the difference between the local sidereal time of a place and the sidereal time in Greenwich , the geographical longitude of this place follows , see astronomical navigation . A measurement of this local sidereal time corresponds to either a location or a time measurement - depending on whether the sidereal time in Greenwich is known at the time of observation or the longitude of the observation location .

Sidereal time and right ascension

The following applies to sidereal time:

The sidereal time is the hour angle of the vernal equinox.
Sidereal time Θ, as well as hour angle τ and right ascension α of a star are linked via the relationship τ = Θ - α.
The sidereal time at a place is the right ascension of the star that is currently culminating (τ = 0).

At the time of the autumn equinox , True Solar Time and Sidereal Time are approximately the same; because a star near the vernal equinox culminates at midnight, when the modern 24-hour counting begins.

Sidereal time and UT

The hour angle of the sun is the true solar time . It can be observed immediately and is indicated by sundials . Because of the inclination of the earth's axis and the ellipticity of the earth's orbit , the true solar time is non-uniform ( main article: equation of time ). In order to obtain a measure of time freed from the equation of time, the so-called fictitious mean sun is considered instead of the true sun , an imaginary point that runs at constant speed along the celestial equator (not the ecliptic). The hour angle of this point is the mean solar time which is not subject to the equation of time . The position of the fictitious mean sun on the celestial equator cannot be determined by observation, but only by calculation.

In an international agreement in 1896, the following expression, determined by Simon Newcomb, for the right ascension of the fictitious central sun was made binding:

{\ displaystyle R_ {U} \, = \, 18 ^ {\ mathrm {h}} \, 38 ^ {\ mathrm {m}} \, 45 {,} 836 ^ {\ mathrm {s}} +8640184 { ,} 542 ^ {\ mathrm {s}} \ cdot T_ {U} +0 {,} 0929 ^ {\ mathrm {s}} \ cdot T_ {U} ^ {2}}

It is the number of since Greenwich mean noon (12 ^h UT) on 0th January 1900 elapsed Julian centuries depending 36,525 mean solar days. The linear term of the equation indicates the speed of the fictitious mean sun with respect to the mean vernal equinox of the date, the quadratic term takes into account the fact that the precession-induced movement of the vernal equinox is currently accelerating slightly. ${\ displaystyle \ textstyle T_ {U}}$

Universal time UT was defined as the Greenwich hour angle of the fictitious mean sun plus 12 hours (the addition of 12 hours is necessary because the meridian passage of the fictitious mean sun is to take place at 12 o'clock UT, but its hour angle at this moment is 0 ^h ). However, the hour angle of an object is equal to the hour angle of the vernal equinox minus the right ascension of the object, and the hour angle of the vernal equinox is by definition nothing other than sidereal time. The relationship between UT and Greenwich sidereal time is:

UT	= 12h + Greenwich hour angle of the fictitious mean sun
	= 12h + Greenwich hour angle of the vernal equinox - R _U
	= 12h + Greenwich sidereal time - R _U

Since the right ascension of the fictitious mean sun given by Newcomb relates to the mean vernal equinox of the date, the sidereal time occurring here is the mean Greenwich sidereal time.

At 12 o'clock UT, the Greenwich sidereal time is identical to R _U (since this is the culmination time of the fictitious central sun with the right ascension R _U ). Therefore, R _{U can} also be regarded as the Greenwich sidereal time corresponding to the time 12 ^h UT. From this follows the expression used from 1900 to 1984 for the mean Greenwich sidereal time: at the time 0 ^h UT of each day is the corresponding mean Greenwich sidereal time

{\ displaystyle \ mathrm {GMST (0 ^ {\ mathrm {h}} \, UT)} \, = \, 6 ^ {\ mathrm {h}} 38 ^ {\ mathrm {m}} 45 {,} 836 ^ {\ mathrm {s}} \, + \, 8640184 {,} 542 ^ {\ mathrm {s}} \ cdot T_ {U} +0 {,} 0929 ^ {\ mathrm {s}} \ cdot T_ { U} ^ {2}}

Here, T _U , starting from the point in time 1900.0, grows successively with a step size of 1/36525. To the particular so for 0h UT Stardate nor since have 0 ^h elapsed UT sidereal hours to add (see below).

With the introduction of improved astronomical constants in 1984, this formula was also revised. The relationship between GMST and UT1 has been redefined as

{\ displaystyle \ mathrm {GMST1 (0 ^ {\ mathrm {h}} \, UT1)} \, = \, 24110 {,} 54841 ^ {\ mathrm {s}} \, + \, 8640184 {,} 812866 ^ {\ mathrm {s}} \, \ cdot \, T_ {U} \, + \, 0 {,} 093104 ^ {\ mathrm {s}} \, \ cdot \, T_ {U} ^ {2} \, - \, {6 {,} 2 \ cdot 10 ^ {- 6}} ^ {\ mathrm {\, s}} \, \ cdot \, T_ {U} ^ {3}}

It is and the number of from 1 January 2000, 12 ^h elapsed UT-day UT1 (JD = 2451545.0 UT1): d _U = ± 0.5, ± 1.5, ± 2.5, ± 3.5, ... ${\ displaystyle T_ {U} = {\ tfrac {d_ {U}} {36525}}}$ ${\ displaystyle d_ {U}}$

The above equations establish a relationship between sidereal time and universal time UT. Although UT should actually be derived from the course of the sun according to its definition, in practice it was derived from the observed meridian passages of stars, i.e. the sidereal time, using these formulas. Star passages can be observed much more precisely than the position of the extremely bright sun that warms the instruments. This definition of UT1 was valid until 2003. Since then, UT1 is no longer determined by sidereal time, but by the newly introduced "Earth rotation angle".

Before the irregularities and the long-term slowdown of the earth's rotation were recognized, sidereal time and the UT derived from it were considered to be strictly uniform time scales. At the beginning of the 20th century, astronomers realized that the two scales were not uniform and had to introduce new, uniform time scales. The time scales derived from the earth's rotation, such as UT, are also referred to as "civil time" and are increasingly deviating from regular time scales such as ephemeris time , atomic time and the like. ( main article: Delta T ).

Calculating the sidereal time

The formulas can also be used to calculate sidereal time from known UT.

Stardate in Greenwich

To do this, first determine the Julian date JD for the time 0 ^h UT on the desired date (a number ending in, 5). Then compute T :

{\ displaystyle T \, = \, {\ frac {JD-2451545 {,} 0} {36525}}}

and thus the mean Greenwich mean sidereal time for 0 ^h UT, as required in time or degree:

{\ displaystyle {\ begin {aligned} \ mathrm {GMST (0h \, UT)} \, & = \, 6 ^ {\ mathrm {h}} 41 ^ {\ mathrm {m}} 50 {,} 54841 ^ {\ mathrm {s}} +8640184 {,} 812866 ^ {\ mathrm {s}} \ cdot T + 0 {,} 093104 ^ {\ mathrm {s}} \ cdot T ^ {2} -0 {,} 0000062 ^ {\ mathrm {s}} \ cdot T ^ {3} \\ & = \, 24110 {,} 54841 ^ {\ mathrm {s}} +8640184 {,} 812866 ^ {\ mathrm {s}} \ cdot T + 0 {,} 093104 ^ {\ mathrm {s}} \ cdot T ^ {2} -0 {,} 0000062 ^ {\ mathrm {s}} \ cdot T ^ {3} \\ & = \, 100 {,} 46061837 ^ {\ circ} +36000 {,} 770053608 ^ {\ circ} \ times T + 0 {,} 000387933 ^ {\ circ} \ times T ^ {2} - (T ^ {3} / 38710000) ^ {\ circ} \ end {aligned}}}

To determine the sidereal time GMST for any point in time UT of the given date, multiply UT by 1.00273790935 (= synodic day length / sidereal day length) and add the result to the previously calculated sidereal time for 0 ^h UT.

Sidereal time at the observer's location

An observer at longitude λ still has to convert to his local sidereal time:

{\ displaystyle {\ begin {alignedat} {2} \ mathrm {LMST} \, & \, = \ mathrm {GMST} + \ lambda / 15 & \ quad & {\ text {if GMST in time}} \\ & \ , = \ mathrm {GMST} + \ lambda && {\ text {if GMST in degrees}} \\\ end {alignedat}}}

If necessary, the LMST angle has to be brought to the main value (0 ° –360 °) and converted into the time measure .

Web links

Online sidereal time calculator

Individual evidence

↑ A great hour is about 0.9973 hours of sunshine .
↑ Since the sun moves through the sky once a year, this “momentary view of the sky” is only a “fictional view of the sky” for about half a year. The celestial bodies contained in it cannot be observed in daylight despite the unchangeable sidereal time.
↑ A. Schödlbauer: Geodetic Astronomy. Walter de Gruyter, Berlin / New York 2000, ISBN 3-11-015148-0 , p. 312.
^ HU Keller: Astrowissen. Kosmos Verlag, Stuttgart 2000, ISBN 3-440-08074-9 , p. 44.
↑ A. Schödlbauer: Geodetic Astronomy. Walter de Gruyter, Berlin / New York 2000, ISBN 3-11-015148-0 , p. 316.
^ DD McCarthy, PK Seidelmann: Time - From Earth Rotation to Atomic Physics. Wiley-VCH Verlag, Weinheim 2009, ISBN 978-3-527-40780-4 , p. 13.
↑ ^a ^b ^c D.D. McCarthy, PK Seidelmann: Time - From Earth Rotation to Atomic Physics. Wiley-VCH Verlag, Weinheim 2009, ISBN 978-3-527-40780-4 , p. 15.
^ S. Aoki, H. Kinoshita, B. Guinot, GH Kaplan, DD McCarthy, PK Seidelmann: The New Definition of Universal Time. Astronomy and Astrophysics, Vol. 105 (1982), No. 2, pp. 359-361 ( bibcode : 1982A & A ... 105..359A ).
^ J. Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1 , chap. 12.

[1] A great hour is about 0.9973 hours of sunshine .

[2] Since the sun moves through the sky once a year, this “momentary view of the sky” is only a “fictional view of the sky” for about half a year. The celestial bodies contained in it cannot be observed in daylight despite the unchangeable sidereal time.

[3] A. Schödlbauer: Geodetic Astronomy. Walter de Gruyter, Berlin / New York 2000, ISBN 3-11-015148-0 , p. 312.

[4] HU Keller: Astrowissen. Kosmos Verlag, Stuttgart 2000, ISBN 3-440-08074-9 , p. 44.

[5] A. Schödlbauer: Geodetic Astronomy. Walter de Gruyter, Berlin / New York 2000, ISBN 3-11-015148-0 , p. 316.

[6] DD McCarthy, PK Seidelmann: Time - From Earth Rotation to Atomic Physics. Wiley-VCH Verlag, Weinheim 2009, ISBN 978-3-527-40780-4 , p. 13.

[McCarthySeidelmannS15-7] D.D. McCarthy, PK Seidelmann: Time - From Earth Rotation to Atomic Physics. Wiley-VCH Verlag, Weinheim 2009, ISBN 978-3-527-40780-4 , p. 15.

[8] S. Aoki, H. Kinoshita, B. Guinot, GH Kaplan, DD McCarthy, PK Seidelmann: The New Definition of Universal Time. Astronomy and Astrophysics, Vol. 105 (1982), No. 2, pp. 359-361 ( bibcode : 1982A & A ... 105..359A ).

[9] J. Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1 , chap. 12.