Astronomical navigation
Astronomical navigation is the umbrella term for all methods of determining position that are based on the measurement of stars ( sun , moon , planets or selected fixed stars ).
Some astronomically supported methods of direction measurement and control are also part of the subject.
Position determination with sextant, chronometer and astronomical almanac
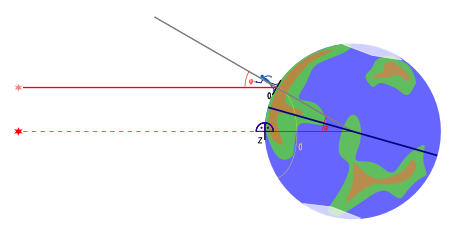
*: Sun (since the distance is many times greater than the size of the earth, the viewing direction for observers in Z and O is parallel within the scope of the measurement accuracy!)
Z: Place over which the sun is at its zenith
O: unknown location of the observer
O ′: set of possible locations of the observer after the first measurement
Principle of the method
With a sextant , a resting observer measures the apparent height of a star (which also includes the sun, moon or planets) above the horizon - at sea above the chimney - the so-called elevation angle h . At the same time, a chronometer or a synchronized stopwatch is used to record the exact time of the measurement in Coordinated Universal Time (UTC).
To determine the position, the complementary angle ζ = 90 ° - h is calculated (i.e. instead of the measurable angular distance to the horizon, the corresponding angle to the zenith is calculated) - the so-called zenith distance .
In tables such as the Nautical Almanac , it is determined over which point Z on the earth's surface the observed star was exactly at the zenith at the time of measurement - the so-called image point (geometrically the base point ). Since the measured elevation angle is normally not 90 °, but 90 ° - ζ , your own location O must be on an arc O with a distance from point Z determined by the angle ζ - i.e. at one of the places where the star below appears at the measured angle. Since angles and distances correspond to each other on the globe, its radius is ζ * 60 nautical miles (1 nm = 1/60 degree).
In order to be able to determine an unambiguous location, the measurement must be repeated with another star (or if the same star is measured with a sufficient time interval). This provides a further point Z 2 and a second circle with a radius determined by ζ 2 . The two circles have two (ideally very distant) points of intersection, of which only one can be considered as a standpoint of its own.
Principle of nautical practice

The two circles of the possible observer locations O ' are plotted and their intersection points are determined.
Note: The circles are shown distorted due to the map projection - if theoretically plotted on a globe, both circles would actually be round! (See also the illustration above) This is (besides the rough scale ) another reason why it is hardly practicable to mark the circles with a compass on the map.
When measuring the same celestial body (e.g. the sun) at different times, it is disadvantageous that measurements are required with a sufficiently long time interval (if possible 3–4 hours or angles> 45 °), since otherwise the stand lines form a grinding angle of intersection and become imprecise. This time interval cannot always be maintained, especially in uncertain weather. In addition, a possible change in location in the meantime ( sails ) must be taken into account - this can be estimated ( cast ) relatively precisely depending on the conditions , but brings additional inaccuracy.
Timely measurements of different stars are therefore cheaper . During the day , bright stars are rarely seen in the sextant, but the moon and Venus are often seen . During the day it is optimal to determine the location with a half moon , because the sun and moon then assume an angle of about 90 ° and both measurements can be carried out promptly during the day. New and full moons, on the other hand, cannot be used to determine the location at sea.
Star measurements are especially possible in the time around sunrise or sunset - until the beginning or end of nautical twilight , in which, in addition to the brighter stars, the horizon, which is indispensable for determining the altitude, remains recognizable. Of the 60 navigation stars contained in the Nautical Almanac , there are always some whose mutual angle is around 90 ° and whose lines therefore intersect well. A third star is recommended as a control. In the procedure that makes sense when using HO-249 Volume 1 “selected stars”, an attempt is made to select three fixed stars whose azimuths differ by 60 °. Such star constellations are highlighted there, as are particularly bright stars. It makes sense to carry out the measurements from east to west during twilight in order to make optimal use of the available time window in which the horizon and the stars are visible, because the stars are first in the east at sunset and the first at sunrise last seen in the west. - To find and identify the stars, the practical “US Star Finder and Identifier No. 2102 D ”issued by the US Navy Hydrographic Office, Washington.
In practice, the problem arises that the circles around the image points of the stars can not usually be drawn on any map with a meaningful scale , since the distances between the image points and the intersection points are usually several thousand nautical miles apart. For example, the image point of the sun moves (depending on the season at different geographical latitudes between the two tropics) at 1667 km / h or 900 kn from east to west.
Therefore, for the actual determination on the high seas , an estimated position (calculation location or cast location ) is first drawn in the nautical chart , or better in a mercator- scaled blank map (see sketches on the right in the pictures) . The azimuth (horizontal angle ) calculated for the estimated position is then drawn in for the image point of the star whose elevation angle has been measured , starting from the estimated position. At the same time, the distance between the image point and the estimated position (calculated height) is calculated and the difference between the calculated height and the observed height (corrected sextant angle) is applied to the azimuth beam starting from the estimated location. The line you are looking for is a circle through this point, with the image point of the star being observed representing the center of the circle. To simplify the construction of the drawing, the segment of the arc is replaced by the tangent to the circle, which is constructed at right angles to the azimuth beam.
The values of the observation of a second star lead to a second straight line, the point of intersection of the two lines is then considered the desired location. If three celestial bodies are observed, the base lines generally form a triangle, the center of which is viewed as the desired location.
For the calculation of the azimuth and the distance to the celestial pixel one needs the theorems of spherical trigonometry , especially those of the nautical triangle . The results of the necessary arithmetic operations can also be determined from multi-volume tables (Pub. 249 or Pub. 229 Sight Reduction Tables for Marine Navigation or for Air Navigation), from the American National Geospatial Intelligence Agency with subsequent interpolation.
Implementation of nautical practice
The above table, which was classified under the term "HO-Tafeln" in merchant shipping, made the calculation of the ship's location a lot easier. Up until the early to mid-1960s, nautical tables ( ephemeris ) were used almost exclusively in practice. and the logarithmic tables “on foot”; a complete location determination using three stars - see right - therefore took about 40 to 45 minutes including the observation. Later, with the HO tables, you could easily do the same thing in about 10 minutes. However, some older captains did not tolerate the new American procedure.
In order to be admitted to captain's courses ( A6 / AG ) at German seafaring schools , legal requirements had to be met with regard to astronomical observations.
- Astronomical navigation on board a sea-going ship - 1963
The navigational officer "shoots" a sun height with the sextant
Lunch cutlery - 4 sun position lines + meridian passage results in lunch on the ship
Astronomical ship location calculation, 3 fixed stars + planet
Astronomical ship location calculation, 2 fixed stars + polar star
Loading the sextant
The angular distance h measured with the sextant between the visible horizon (the so-called chimney ) and the star must be corrected several times before it can be used to calculate the position:
- When observing the sun and moon , half the diameter (approx. 16 ') of the star has to be added or subtracted, depending on whether you have observed the lower or upper edge.
- The height of the observer above sea level, the so-called eye height - this is what makes the notch visible in the first place - means that an angle that is too large is measured (the notch depth ).
- The light rays of the stars are refracted in the atmosphere. This effect is called refraction , here specifically astronomical refraction and it is stronger the lower the star is (the closer to the rear sight). When the sun appears to be setting , it is actually about 0.6 ° lower. The refraction increases strongly for small angles (at 5 degrees around 10 ') and depends on the air temperature and pressure. For this reason, the navigator has limited confidence in a measurement at a notch distance below 10 degrees.
- The formula ζ = 90 ° - h only applies to objects that are infinitely distant. The error caused by this is called horizontal parallax . It is negligible for astronavigation with the sun and fixed stars, but not for the planets (corrections up to about 0.5 ′) and especially for the moon (up to 1 ° 02 ′).
Values for these corrections can also be found as tables in the nautical almanac, which are referred to as "total loading for the chiming distance of the lower edge of the sun", "total loading for the chiming distance of a fixed star or planet" and "total loading for the chiming distance of the lunar lower edge" and "additional loads".
With the help of a clock accurate to the second, the current almanac and a commercially available sextant, an experienced observer can achieve a star measurement accuracy of 1 'and in the position 1–2 nautical miles under ideal conditions. In practice, the conditions are rarely ideal:

- On board ships, you stand on a slightly swaying surface. The marine or mirror sextant can compensate for this for the most part (star and rear sight remain almost in cover), but only as long as they do not wobble out of the field of vision.
- Clouds and haze often obstruct the view of the stars. Astronavigation is only possible when the sky is at least partially open. The horse latitudes (15–30 ° latitude ) and high latitudes are cheaper than average .
The 60 navigation stars in the almanac are sufficient even when it is half cloudy, but they are not always identifiable. - The night sky by the sea is not significantly brighter than the notch , so that height measurements are uncertain - even if the notch is apparently clearly visible . With normal sextants, stars and planets can therefore only be measured precisely at dawn and dusk. A bladder sextant (with a mirrored, illuminated dragonfly ) can help.
- Low-lying stars are easier to find in the sextant than high ones, but less reliable for the calculation.
A practical example shows the calculation / sketch on the right. - Here you can immediately see that the coupling location Og and the observed location Ob are far apart. - This is the observation result after 3 days of persistently bad weather (winter North Atlantic) with closed cloud cover and no possibility of astronomical location determination. - This example alone makes it clear why in distress at sea it could sometimes lead to incorrect position information , with location deviations of 10, 20 and more nautical miles. - The Spiegel article 1958 about the sinking of the sailing school ship Pamir , which u. a. also busy with the incorrect position information.
Complementary procedures
Determination of latitude
The geographical latitude can also be determined directly by measuring the highest level of the sun (so-called lunch cutlery ) or a prominent fixed star ( upper culmination) . Until the invention of the sextant , this was done with the Jacob's staff . In calm weather and a clearly recognizable horizon an accuracy of about one arc minute (1/60 degrees) can be achieved with modern sextant, resulting in position one nautical mile corresponds to (1852 m). This form of astronomical navigation is also called latitude sailing and the result is called midday latitude.
The Pole Star takes on a special role among the stars, because north of the Earth's equator, due to its location near the celestial pole, it is visible throughout the night, easily identifiable and sufficiently bright. From the measured elevation angle of the Polar Star, the latitude is obtained immediately after only a few mathematical corrections (maximum 0.9 °).
If one observes the upper culmination of a star, one speaks of a meridian width . It is also easy to evaluate (simplified Sterneck method ) and if the south direction is not exactly known, the measurements can also be carried out in a circumsidian .
Determination of longitude
The determination of the geographical longitude is only possible with the help of an exact time measurement, and has gone down in the history of seafaring as the longitude problem . The orientation of the starry sky depends on the day, world time and longitude. If the date and time (UTC) are known, the length is obtained from the star position.
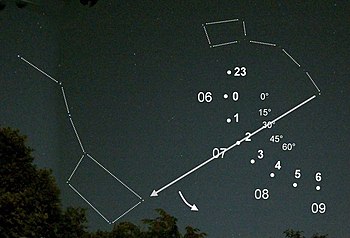
Example 1: At the starting point at 2:00 a.m. solar time, the circumpolar Big Dipper is oriented as in the picture. At other longitude positions it appears rotated according to the longitude angle: If it is 30 ° more east, it is at position 4, at 30 ° west at position 0.
Example 2: Along one degree of latitude, the same position of the Big Dipper is reached at other times. A difference of one degree of longitude causes a time difference of 24h / 360 °, i.e. 4 minutes. For example, if the Big Dipper does not reach the position until 3:00 a.m., you are 15 ° west of the starting point.
If you observe the time of the sun's culmination from its elevation angle , you can determine the length of your own location from the nautical almanac . Because the sun's path is almost horizontal at noon, the culmination can only be determined with sufficient accuracy by averaging two times of the same sun height before and after the culmination. If the observer has moved between these two points in time, corrections for the second solar height are necessary, especially for north-south change of location (see sailing ).
Four times a year (April 16, June 14, September 1 and December 25) the equation of time is zero. Around these days, the length can be determined without additional tables - only from the highest level of the sun and UTC world time.
The length problem could be before the invention of the ship chronometer only approximately with Tobias Mayer's method of lunar distances solve, but at best, on tenth of a degree. Because
- the lunar orbit is subject to numerous disturbances that are difficult to calculate,
- and only moves by its diameter every hour;
- The position of the measuring device, with which the small angle between the moon and star is measured, can only be determined by trial and error and therefore imprecisely.
Further development and modern positioning
It was not until the end of the 19th century that high-precision, robust watches had become so cheap that every captain could afford one, and the principle of time measurement finally prevailed over Mayer's method of lunar distances. Since the earth moves at approx. 463 m / s at the equator, a clock error of 1 s causes a position error of up to 463 m. With the introduction of shortwave radio , time information (time signals) accurate to the second could be received on the high seas with simple radio devices , which further improved position determination . Today the navigator uses the height difference method according to Marcq Saint-Hilaire to determine its position : The height of a star above the horizon is calculated for the coupling point at the time of measurement.
The level line (the line on the earth's surface from which all observers measure the same elevation angle for a certain star) is a circle on the earth's surface. All observers on this line are equidistant from the image point, the place where the connecting line between the star and the center of the earth pierces the surface of the earth. Due to the large radius of these circles, the level can be assumed to be a straight line in practice if the elevation angle of the star above the horizon is less than 85 °. This results in a baseline. If you cut the stand lines of several stars, you get a true place. If you z. For example, if during the day only the sun is available as the only celestial body, you “sail” the stance line, thus shifting it along the course by the distance covered until you get another stance line with which this can be brought to the intersection. This “sailing” can be applied to all types of base lines (see navigation ).
Nowadays ships use navigation satellite systems for navigation , but means for determining position using astronomical methods (i.e. tables and devices) are still required. After a break of about ten years, the US Navy has been teaching navigators again since 2011, and all officers since autumn 2015, in astronomical navigation.
See also
- Navigation star
- Length clock , astrolabe , sextant
- GPS , GLONASS , Galileo
- Dead reckoning , bearing to Polarstern
- interplanetary navigation
- Space Sextant , spatial position
- Astronomical Inertial Navigation
literature
- Dava Sobel : Longitude . btb paperback, 1998. ISBN 3-442-72318-3 . (Orig .: Longitude , 1995)
- Frank Mestemacher: Astronomical Navigation. Not just to arrive. Kruse, Stralsund 2013, ISBN 978-3-941444-87-4
- Wolf Nebe: Practice of astronavigation. Explanation of the basics using colored graphics; quick location determination through clearly structured instructions. Delius Klasing, Bielefeld 1997, ISBN 3-7688-0984-6
- Bobby Schenk : Astronavigation. Delius Klasing, Bielefeld 2000, ISBN 3-7688-0259-0
- Gerhard Meyer-Uhl: Practical astronavigation with circumnavigators. (= BLV-Bordpraxis, No. 7) BLV-Verlagsgesellschaft, Munich / Vienna / Zurich 1980. ISBN 3-405-12219-8
- Karl-Richard Albrand: Astronomical Navigation Today. (= Up to date, further training on board, no. 24) Published by the Sozialwerk für Seeleute e. V., Hamburg. New revised edition, status 1991. Hamburg: Sfs, 1991
- Mary Blewitt: Practical Navigating for Stars. Delius Klasing, Bielefeld 1992, ISBN 978-3-87412-033-3
- Walter Stein ; Werner Kumm: Astronomical Navigation. ( Yacht Library , Volume 88) 11th edition. Delius Klasing, Bielefeld 2002, ISBN 3-87412-138-0
- Werner F. Schmidt: Astronomical Navigation. A teaching and handbook for students and practitioners. 2nd Edition. Springer, Berlin / Heidelberg / New York / Barcelona / Budapest / Hong Kong / London / Milan / Paris / Santa Clara / Singapore / Tokyo 1996, ISBN 3-540-60337-9
- Winfried Böhm: Manual of Navigation - Terms, formulas, procedures, schemes. Bussesche Verlagshandlung, Herford 1978, ISBN 3-87120-323-8
- Joachim Böhme, Walter Steinfatt, Lothar Uhlig: Astronomical Navigation. (= Guide to navigation). 4th edition. Transpress Verlag for Transport, Berlin 1987, ISBN 3-344-00000-4
- CS Draper: Space navigation - guidance and control. Mackay, London 1966
- Edward V. Stearns: Navigation and guidance in space. Prentice-Hall, Englewood Cliffs NJ 1963
- Hasso Eichel: Location determination according to the stars. Franckh'sche Verlagshandlung, Stuttgart 1962
- Robert A. Park, Thomas Magness: Interplanetary navigation - principles and methods for journeys to other planets. Holt, Rinehart and Winston, New York 1964
- Erwin Schrödinger ; P. Jordan; H. Siedentopf: Orientation in space. (= The international forum, issue 3). Fontana-Verlag, Zurich 1954
- Markus Werthmann: Astronavigation. Dipl.-Arb., University of Innsbruck, 2008
- Sergejs Slaucitajs: On astronomical navigation in high latitudes = On astronomical navigation in high latitudes. (= Contributions of Baltic University, Nor.14) Baltic University, Pinneberg 1947. 16 pages
Web links
- Step-by-step guide to astronomical navigation
- Astronavigation while sailing
- Ephemeris and Star Positions
Individual evidence
- ↑ see in the English Wikipedia
- ↑ Maritime Safety Information. In: msi.nga.mil , accessed November 15, 2012
- ↑ The Fall of the Pamir, Three Questions . In: Der Spiegel . No. 30 , 1958 ( online ).
- ^ Tim Prudente: Seeing stars, again: Naval Academy reinstates celestial navigation. In: Capital Gazette , October 12, 2015; accessed on October 15, 2015



