Jacob's staff

The title of this article is ambiguous. The Jacob's staff is also a pilgrim's staff and used to be a name for the Orion belt in the constellation Orion.

Jacob's staff of the 17th century ( Kunstkammer in the State Museum Stuttgart )

Angle measurement with Jacob's staff
( Peter Apian , Introductio geographica , 1523)

A Jacob's staff (Latin baculus Jacobi ), also a ruler or cross staff , is an earlier astronomical instrument for angle measurement and for indirect distance measurement . It was mainly used in seafaring , but also in land surveying and astronomy. The Jacob's staff was the forerunner of the sextant in nautical science .

The invention of the Jacob's staff, which is easier to handle at sea than the astrolabe , dates back to the 13th century and is even similar to a sighting device developed by Avicenna in the 11th century, but it was Johannes Müller, known as Regiomontanus , who made the instrument into one in the 15th century popular measuring device.

Name and appearance

The name of the bar comes from a certain resemblance to the designated also as "Jacob's staff" pilgrim's staff of pilgrims .

The Jacob's staff consists of a basic staff with a reading scale and several cross pieces of wood, one or two of which are used for a measurement, the selection of which depends on the required angular range. The crossbars give it a crossbow- like appearance, which is why it is said to this day when the sextant is used: you shoot a star when you measure its height above the horizon.

application

Angle measurement

Determination of the elevation angle of a star

In seafaring, the device was mainly used to determine the geographical latitude . For this purpose, the elevation angle of the sun or a fixed star (mostly the Pole Star ) was measured above the nautical horizon . In coastal navigation, it was also used to measure angles between terrestrial targets and thus determine one's own position on the map.

It is used by attaching the longitudinal rod to the cheekbone under the eye and then moving the cross piece until its ends just cover the horizon and the targeted star or target. Half the length of the cross bar, divided by the length read on the main bar (distance from the eye to the cross bar), gives the tangent of half the desired angle between the horizon and the star. The longitudinal bar was often scaled in such a way that the angle for a certain cross bar length could be read off directly.

It is difficult to use because the two bearings have to be maintained at the same time while the transverse rod is being moved across the scale , which can hardly be carried out with the desired accuracy, especially on a swaying ship.

Calculating the distance or distance

You can also measure the height or the distance of an object with the help of Jacob's staff, if the other value is known.

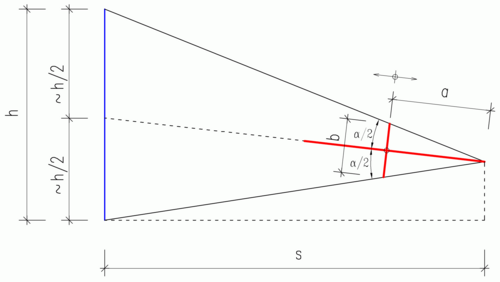
The following applies to all: = the distance to the object ${\displaystyle s}$

${\displaystyle h}$ = the height of the object

${\displaystyle h_{a}}$ = eye level

${\displaystyle a}$ = the distance from the runner to the eye

${\displaystyle b}$ = the length of the runner

Approximation formula

Jacob's staff

If spacing can be easier to apply with good approximation the following formulas: The distance is at a given height : ${\displaystyle s}$ ${\displaystyle h}$

${\displaystyle s\approx {\frac {h}{2}}\cdot \cot {\frac {\alpha }{2}}}$

or

${\displaystyle s\approx h\cdot \cot \alpha }$

or

${\displaystyle s\approx {\frac {h}{2\cdot \tan {\frac {\alpha }{2}}}}}$

or

${\displaystyle s\approx {\frac {h}{\tan \alpha }}}$

The height is at a given distance : ${\displaystyle h}$ ${\displaystyle s}$

${\displaystyle h\approx 2s\cdot \tan {\frac {\alpha }{2}}}$

or

${\displaystyle h\approx s\cdot \tan \alpha }$

Apian's method

Jacob's staff

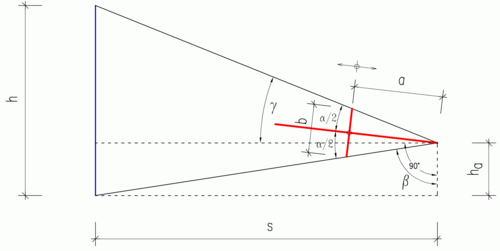
The mathematician Philipp Apian (1531–1589) described a method to use the Jacob's staff to determine the height of the object. According to him, one must hold Jacob's staff to the eye so that the upper end of the runner can be seen at the upper end of the object and the lower end accordingly at the lower end of the object. Then, according to Apian, the height of the object is calculated using the following formula: ${\displaystyle h}$

${\displaystyle h\approx {\frac {s\cdot b}{a}}}$

For this calculation, Philipp Apian uses the 2nd theorem of rays. The conditions for this sentence are not always fulfilled here, however, because the runner is not necessarily parallel to the object. However, this error has only minor effects over long distances.

Exact determination (runner parallel to the object)

Jacob's rod, the theorem of rays says: ${\displaystyle {\tfrac {h-h_{a}}{b/2}}={\tfrac {s}{a}}}$

There are two ways to determine the exact height. The first is the simpler one, it is based on the theorem of rays and does not require any angle functions. You have to hold the Jacob's staff so that the runner is parallel to the object and you can see the upper end of the runner at the top of the object. Then the formula for calculating the height is : ${\displaystyle h}$

${\displaystyle h=h_{a}+{\frac {s\cdot b}{2a}}}$

Exact determination (general case)

Jacob's staff

The second method is a little more complicated because it uses trigonometric functions. The staff of Jacob has to be held again, as described by Philipp Apian. Here too, eye level is required. ${\displaystyle h_{a}}$

Solution over ${\displaystyle \arctan }$

${\displaystyle h=h_{a}+s\cdot \tan \left({2\cdot \arctan {\frac {b}{2a}}+\arctan {\frac {s}{h_{a}}}-90^{\circ }}\right)}$

Solution over ${\displaystyle \arccos }$

${\displaystyle h=h_{a}+s\cdot \tan \left({2\cdot \arccos {\frac {a}{\sqrt {a^{2}+\left({\frac {b}{2}}\right)^{2}}}}+\arccos {\frac {h_{a}}{\sqrt {s^{2}+h_{a}^{2}}}}-90^{\circ }}\right)}$

The advantage of the second method is that you don't have to pay attention to whether the runner is parallel to the object and the Jacob's staff is thus parallel to the ground. For this, this formula is difficult to memorize.

See also

• Stick bearing
• Jump of the thumb
• Bussole - compass with bearing device
• Theodolite - instrument for land surveying

literature

• Franz Adrian Dreier: angle measuring instruments. From the 16th to the early 19th century. Kunstgewerbemuseum, Berlin 1979 (exhibition catalog, Berlin, Kunstgewerbemuseum, November 9, 1979 - February 23, 1980).
• Willem FJ Mörzer Bruyns: The Cross-Staff. History and Development of a Navigational Instrument. Vereeniging Nederlandsch Historisch Scheepvaart Museum, Zutphen 1994, ISBN 90-6011-907-X ( Vereeniging Nederlandsch Historisch Scheepvaart Museum. Jaarboek 1994).
• Albert Schück: The Jacob's staff. In: Annual report of the Geographical Society Munich. Issue 2, 1894/1895, ISSN  0938-2097 , pp. 93-174.

Web links

Commons : Jacob's staff  - collection of pictures, videos and audio files

• The Jacob's staff, angle measuring instrument of the ancient seafarers
• Information page of the TU Freiberg
• Information page of the Maritime Museum of the Oldenburg Weser Ports ( Memento from February 7, 2008 in the Internet Archive )
• Gabriele Rettenmaier: Measuring in Geometry. (PDF; 2.42 MB) Script from the Weingarten University of Education. 

Individual evidence

1. ^ Gotthard Strohmaier : Avicenna. Beck, Munich 1999. ISBN 3-406-41946-1 , p. 157.
2. ↑ Ralf Kern: Scientific instruments in their time. From astrolabe to mathematical cutlery . Cologne: Verlag der Buchhandlung Walther König, 2010. S. 214.