Filter (electrical engineering)
In electrical engineering and communications engineering, circuits are referred to as filters (in technical language mostly the / a filter ) , which change an electrical signal in amplitude and phase position depending on the frequency . This can weaken or suppress unwanted signal components.

Classification and Applications
Filters can be classified according to several criteria, for example according to their complexity, their frequency response, the components used, the circuit structure, the calculation method used, the selectivity or steepness in the stop band and the phase shift.
Filters in the classic sense, such as low or high pass , change the frequency response . They are also called filter circuits . Circuits and processes that change more complex properties such as phase position , impedance and noise components are also summarized under the term filter . In sound engineering , digital and analog frequency filters (filters) are also known as equalizers ( EQ for short ) and are used as sound effects . This also includes presence , absence , band pass , high pass and low pass filters .
Well-known applications are:
- Radio / radio : Selection of a specific transmission frequency to receive a station. Only the set frequency is received. All other frequencies are filtered out.
- Loudspeaker crossover: The different frequencies for highs, lows and midrange are split up and distributed to the corresponding loudspeakers .
- Line filter : They suppress crackling when switching on other loads and other interference
- DSL splitter , the low-frequency telephone signals and DSL separate
- Measurement value processing in mechanical engineering, the automotive industry, aerospace technology
history
The foundations of the theory of electrical filters were developed in 1915 by the German communications engineer Karl Willy Wagner and the American communications engineer George Ashley Campbell .
Frequency filter
Frequency filters are circuits (called “ networks ”) with predetermined frequency-dependent transmission behavior (frequency response), which suppress certain frequency ranges of the input signal (stop range) and / or transmit other ranges with preference; see transmission range .
Parameters
All characteristics of a linear filter are described by the frequency response or generally by the transfer function. The key factor here is the characteristic frequency f c (center frequency) and, in the case of bandpass filters / blocks, the filter quality Q. In most cases, f c is not equal to f 3 , the cutoff frequency at which the amplitude has decreased by 3 dB . This is discussed in detail in Tietze / Schenk (see literature).
Transfer functions of filters
Regardless of the specific implementation of the filter (whether analog or time-discrete or digital ), the functionality of a filter can be described by its transfer function. This determines how the input signal is changed in amplitude and phase angle .
Transfer functions of analog filters
When designing the filters, they should be based on the desired transfer function. When choosing the transfer function of multi-pole analog filters, various optimized frequency responses for analog filters have proven to be effective , depending on the desired filter characteristics :
| Filter characteristic | properties | advantages | disadvantage |
|---|---|---|---|
| Butterworth filter | Maximum flat course of the absolute frequency response in the pass band, attenuation in the stop band running monotonously | Good amplitude behavior in the passband and stopband | Low slope in the transition area |
| Legendre filter | Flat course of the absolute frequency response in the pass band, attenuation in the stop band running monotonously | Compromise between Butterworth filter and Chebyshev filter | |
| Chebyshev filter | Ripple in the pass band, attenuation in the stop band running monotonously | Good slope in the pass band | Big change in group delay , poor timing |
| Inverse Chebyshev filters | Monotonous progression in the pass band, ripple in the stop band | Good slope in the pass band | Big change in group delay, poor timing |
|
Bessel filter also known as Thomson filter |
Pulse shaping | Constant group delay (= linear phase) in the passband | Low slope in the transition area |
|
Cauer filter also known as an elliptical filter |
Ripple in the pass and cut areas | Very good edge steepness in the transition area | Big change in group delay, poor timing |
| Gaussian filter | Pulse shaping | Constant group delay in the pass and blocked areas. No overshoot in the step response. Reduced intersymbol interference | Low slope in the transition area |
| Raised cosine filter | Pulse shaping, Nyquist filter | No intersymbol interference | Low slope in the transition area |
|
TBT filter Transitional Butterworth-Thomson filter |
Pulse shaping | Unit jump response between Butterworth and Thomson behavior | More overshoots than Thomson filters |
Adaptive filters
Normal filters have a fixed characteristic frequency f c (for example to eliminate interference from the 50 Hz mains frequency or its multiple). If the interference varies in frequency, adaptive filters can be used to improve the signal-to-noise ratio .
Transfer functions of digital filters
These transfer functions, which are primarily used in analog filter structures, can, with minor adjustments, also be transferred to digital filters in the structure of IIR filters . The adjustments concern the essential fact that digital filters work with temporally discrete values and thus a finite base bandwidth .
Transfer functions not causal filters
In addition, other transfer functions can be used, which are designed according to the application.
Their transfer function is not causal . They follow a final law that not only takes instantaneous values into account , but also their course . The transfer function plays an essential role in filter theory because of its simple structure and model character . The simplest examples are theoretical transfer functions which cannot be implemented in practice, such as those of the ideal low-pass filter .
order
The order of a filter describes the decrease in gain ( attenuation and edge steepness ) of frequencies (far) above or below the respective cut-off frequency of the filter. In the case of low-pass or high-pass filters, it is approximately n * 6 dB per octave (n * 20 dB per decade ) over the frequency , where n represents the order of the filter. For bandpass filters or bandstop filters, which represent combinations of low-pass and high-pass filters and thus have two filter edges, the filter order as a function of the steepness of the filter edge is twice as high: A 4th order bandpass sometimes has 40 dB per decade. The filter quality Q is decisive .
Higher-order filters can either be implemented by connecting lower-order filters (1st and 2nd order) in series or by means of appropriate circuits.
The transfer function is:
With
- DC voltage gain
- Filter coefficients
- with as the cutoff frequency
- n order of the filter
Filter types
Filter and frequency response, selection behavior
The theoretical standard cases of the selection behavior of a filter are:
- A low-pass filter weakens the high frequencies up to a cut-off frequency and allows all lower frequencies to pass with practically no attenuation (gain = 1). This "low pass" is used for B. as anti-aliasing filter (see aliasing effect ) or for noise reduction.
- A high-pass filter attenuates the low frequencies up to a cut-off frequency, while all higher frequencies (with a gain of 1) are allowed through. This “high pass” can be used to suppress DC voltage components or slow drifting in the signal.
- A bandpass filter attenuates all frequencies outside of a frequency interval that is defined by two cutoff frequencies. Amplitude or frequency modulated signals carry most of their information in a limited frequency band. A band pass allows this part of the mixed frequencies to pass and blocks the parts below and above the cut-off frequencies. Bandpass filters are also called band filters for short and are used, for example, in the high frequency range of a superhet radio receiver to select the intermediate frequency .
- A bandstop filter ( suction circuit , notch filter , bandstop filter) is the inverse of the bandpass filter. Only frequencies within a frequency interval that is defined by two cutoff frequencies are attenuated. Fixed frequency interference, such as network frequency interference or radiation from radio transmitters, can be removed more or less effectively from the signal.
- An all-pass filter lets all frequencies through to the output with the same gain. A frequency-dependent phase shift or an impedance transformation can be carried out with all-passes .
- A multi -rate filter (such as a CIC filter ) is used in digital signal processing to convert signal sequences between different sampling rates . It is used to suppress aliasing and to avoid mirror spectra.
However, the ideal case of a rectangular or step-shaped transfer function cannot be achieved in practice. In the context of the filter design for determining the filter parameters, a standardized low-pass filter is usually assumed. As a result, the determined filter coefficients are converted to the actual filter type of the target system by means of filter transformations such as the low-pass-high-pass transformation or a low-pass-bandpass transformation .
Corresponding types of filters are used both in the low frequency range (e.g. audio technology) and in the high frequency range (e.g. broadcast technology).
Parametric filters can be set in one or more parameters (frequency, quality) and can usually be operated as a low-pass, high-pass or band-pass filter. Areas of application are mixing consoles and audio technology.
Linear and non-linear filters
Linear filters
With a linear filter, the filtering properties are independent of the signal level. The signal is not distorted. If you increase the input signal for a certain frequency by a factor a, the output signal for this frequency is also increased accordingly. The form of the signal is not fundamentally changed. Low-pass, high-pass, band-pass, band-stop and all-pass are called linear filters. But there are also much more complex linear filters. For example, an echo effect or a comb filter is also linear.
They can be shown as a four-pole equivalent circuit diagram.
Nonlinear Filters
In the case of a non-linear filter, the properties of the filtering are dependent on the signal level and the signal over time. The signal is distorted in its form. The non-linear filters include, for example, limiters, distorters, rectifiers (amount) and median filters .
Passive and active filters
Passive filters
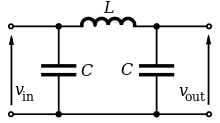
Passive filters are based on combinations of resistors (R), coils (L), capacitors (C) or, for example, crystals (Q) or ceramic elements. For example, filters from RC , RL, LC, LCQ or RCL combinations can be implemented.
Since these filters can work without an external power supply, these combinations are called “passive filters”. Depending on the structure of the network, the filters act as low-pass, band-pass, high-pass, band-stop or all-pass filters.
In many filter applications, a sharp transition of the transfer function from the pass band to the stop band is desirable. The "sharpness" is indicated by the quality factor Q of the filter. The greater the quality, the greater the attenuation in the blocking range per decade. The degree and type of transfer function, and thus also the number and quality of the components of the filter, as well as the costs for implementation, depend on the desired quality.
Passive filters are often named according to the nature of their transfer function, e.g. B. Bessel, Chebyshev, Cauer filters. They are particularly suitable for filtering tasks in the range of high frequencies and high powers as well as in all applications where low self-noise and high linearity are important. A special form of passive filters, filters with waveguides realized waveguide filter is because there are no discrete components are used, but the filter characteristic is given by the geometry of the structure.
Examples of the use of passive filters are:
- PLC filters in high voltage lines
- Suction circuit
- Intermediate circuit
- Harmonic filter
- Line filter
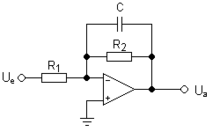
Active filters or electronic filters
In addition to passive components, active filters also consist of active components such as B. transistors or operational amplifiers (OPV). Active filters therefore always need their own power supply. When implementing active filters, in addition to the active components, only resistors (R) and capacitors (C) are often used. In this case, such a filter is also called an active RC filter . An active, analog filter of the second order with an operational amplifier and several resistors and capacitors with a particularly simple circuit structure is called a Sallen-Key filter .
With active components, inductances can be simulated ( gyrator ), which means that large coils can be dispensed with, especially at low frequencies (<1 kHz). Active filters have the advantage that high quality levels can be achieved by doing without coils.
In addition, the active components allow an easy-to-integrate amplification of the signal, so that active filters also act as amplifiers. But this is not a mandatory combination.
Analog filters
A filter is called an analog filter if it processes the signals continuously in terms of time and amplitude.
Digital filters and digital signal processors (DSP)
The digital filters can be classified according to the type of input or output signal; it is taken into account whether these are available analog or digital and are further processed. In the first case, the input signal must be digitized via an A / D converter before it can be processed. After processing, the signal must be converted again using a D / A converter .
By processing digitized signals either with signal processors or with computers, a flexibility is achieved that cannot be achieved by any other type of filter. The flexibility lies in the fact that the filter is modeled by a data set that can be changed relatively easily. In this way, all of the above filter types can be implemented with one filter without having to make changes to the hardware.
The latency period , which is often cited as a disadvantage , which is caused by the AD and DA conversion, can now be neglected, as it is only a few samples with conventional converters. By using a higher sampling rate (96 kHz), this can be shortened again, as z. B. in DA converters, a low-pass filter with a lower slope can be selected in favor of a lower latency.
Digital filters can process the signal either in the time domain (analogous to the other types of filter) or in the frequency domain .
In the time domain, the advantage of digital filters is the lack of component tolerance and aging of the components.
The filters can be designed very flexibly in the frequency range; in particular, these filters can be adapted much more easily to the existing conditions, since the filter is available as a data set.
The transformation between the time domain and the frequency domain (and vice versa) can be carried out using the Fourier or Laplace transformation , among other things .
Digital filters are used, for example, in
- Audio technology (for example with real-time DSP ) as an effects device
- Video technology
- Radio technology
Furthermore, any procedure that reproducibly assigns a defined output signal to a digital or analog input signal can be understood as a digital filter, e.g. B. ciphers or the filter functions in audio programs or image processing programs.
With digital filters, signals can be calculated not only in real time but also independently of their use. For example, it is possible to use very complex edits to restore old recordings.
Sound characteristics of complex environments can be impressed on a sound signal by convolution .
See also: FIR filter
Other filters
- Quartz filter
- In the 1930s, engineers discovered that different quartz crystals can resonate at acoustic frequencies. Nowadays, crystals are mainly used at much higher frequencies. The advantage of quartz over other hard materials is the piezoelectric effect , which made it possible to convert mechanical vibrations directly into electrical ones and vice versa. They therefore represent a design of a mechanical filter . Furthermore, quartz crystals have a low thermal expansion, so that the frequency over remains constant over a wide temperature range. Quartz filters have a significantly higher quality than LCR elements. If an even higher quality is required, the crystals can also be temperature- stabilized or connected in series.
- Ceramic filter
- The functional principle of ceramic filters, also called dielectric filters, is similar to that of quartz filters and consists of special ceramic ; Like the quartz filters, they are also a type of mechanical filter. They have poorer technical properties, but are much cheaper to produce. They are mainly used in the intermediate frequency range of analog radio receivers.
- YIG filter
- Are filters for microwaves in the range of a few GHz that can be adjusted using a magnetic field .
- Atom filter
- The natural vibrations of atoms and molecules can be used to implement filters at very high frequencies . This is z. B. used in the atomic clock . These filters have extremely high quality factors.
- Switched capacitor filter
- In the case of the switched capacitor filter , several capacitors are connected by electronic switches and, together with resistors, form a switching network. The clock frequency with which the switches are switched has a direct influence on the frequency response . It must be significantly higher than the highest frequency to be filtered.
- AOW filter / SAW filter
- Acoustic surface wave filters , also known as AOW or SAW filters, are based on the interference of signals with different transit times , implemented with the piezo effect . High quality levels can be achieved; Mostly designed as a bandpass filter with a low bandwidth of a few MHz and are therefore mainly used in mobile data transmission.
- BAW filter
- BAW filters ( engl. Bulk acoustic wave ) are also on the piezoelectric effect based filters on CMOS technology are prepared and compared with the SAW filters crucial electrical and physical advantages.
- Raised cosine filter
- Raised cosine filters are realizable pulse shape filters with a flat edge that meet the first Nyquist condition and do not generate any intersymbol interference (ISI).
Individual evidence
- ↑ Duden: Filters
- ↑ Gottfried Fritzsche, Volkmar Seidel: Active RC circuits in electronics. Hüthig Verlag, Heidelberg 1981, ISBN 3-7785-0733-8 .
literature
- Karl-Dirk Kammeyer : message transmission . 4th, revised and supplemented edition. Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8351-0179-1 .
- Karl-Dirk Kammeyer, Kristian Kroschel: Digital signal processing. Filtering and Spectral Analysis . 7th, enlarged and corrected edition. Vieweg + Teubner, Wiesbaden 2009, ISBN 978-3-8348-0610-9 .
- Ulrich Tietze, Christoph Schenk: Semiconductor circuit technology. 8th edition. Springer-Verlag, 1986, ISBN 3-540-16720-X (with detailed tables for the filter coefficients of cascaded Sallen-Key filters up to the 10th order)
- Adel S. Sedra, Peter O. Bracket: Filter Theory and Design: Active and Passive. Matrix Publishers, Beaverton, Oregon 1978, ISBN 0-916460-14-2 .

![A [P] = {\ frac {A_ {0}} {\ sum _ {{i = 0}} ^ {{n}} c_ {i} P ^ {i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/073ac4d47ca8dc9852bd67a00937efa7da24ace9)