Mechanical filter

In the context of signal processing, a mechanical filter is an analog filter which, like electrical filters, is used to select and suppress certain frequency components from the spectrum of a signal . In contrast to electrical filters, the filter effect is achieved through mechanical vibrations of appropriately designed masses . Mechanical filters fall into the field of acoustics , even if the frequencies processed with them do not have to be audible. The interface between the electrical and mechanical system is represented by transducers , which convert the electrical vibrations supplied into mechanical vibrations at the input and the mechanical vibrations back into electrical vibrations at the output.

General

Mechanical intermediate frequency filter for 455 kHz from a radio receiver

Filter module MF200 with torsion resonators from a carrier frequency system

The methods and mathematical procedures from electrical circuit technology can be used directly to calculate mechanical filters. In particular, the filter design methods known and established from electrical network analysis , as well as the methods with two ports , can be transferred directly to corresponding mechanical systems.

In addition to steel and various metal alloys, such as iron-nickel alloys , ceramic materials or quartz are also used as materials . Mechanical filters are further subdivided according to structure and application, such as surface acoustic wave filters (SAW filters), filters miniaturized in microsystem technology (MEMS) and the quartz crystals and ceramic resonators used in the feedback circuit in resonance circuits .

With mechanical filters, very high filter quality can be achieved compared to passive analog filters . This follows from the fact that, in electrical systems, coils with high inductance and at the same time very low ohmic resistances , which represent losses, can only be produced with great effort or not at all. With mechanical filters and their comparatively high quality factor Q - values over 10,000 are common - resonance circuits with high frequency selectivity can be implemented. It is to this fact that the quartz oscillator in electrical oscillating circuits for frequency generation, for example in quartz watches , owes its high frequency stability and accuracy compared to LC oscillating circuits .

historical development

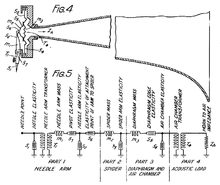
Mechanical filter and its electrical " equivalent circuit " from a gramophone

Mechanical filters do not necessarily depend on an electrical interface and the necessary converters. For example, speaker boxes can be calculated without the electrical system. The first mechanical filters were developed in the 1920s with the then emerging gramophone as purely mechanical systems without an electrical interface.

In the 1950s, mechanical filters began to be realized as an independent filter module because of the high quality factors compared to LC filters, as shown in the figure above as an intermediate frequency filter for 455 kHz in radio devices of that time.

Electrical converters

Types of transducers: (a) A metal rod made of magnetoresistive material. (b) and (c) Cylindrical resonance transducer made of piezometerial shown in green, which is embedded between the electrodes for longitudinal and transverse waves .

The electrical transducers in mechanical filters are usually based on two effects, although transducers are not limited to them: magnetostriction and piezoelectricity . The quantum mechanical effect of magnetostriction uses the fact that a magnetic flux through a suitable material leads to a change in length. In most cases, a “magnetic preload” in the form of a permanent magnet is also necessary, which is why newer and smaller converters almost exclusively use piezoelectric converters made of lead-zirconate-titanate (PZT) or quartz . In addition, with these converter types, the piezoelectric material can be integrated as an essential part of the mechanical filter system, as is the case, for example, with SAW filters or with resonators such as quartz crystals.

construction

Mechanical filters are passive filters . Electrical passive filters are formed from ohmic resistors with an electrical resistance , capacitors with an electrical capacitance and coils with an inductance . In the mechanical system corresponds to the electrical resistance R , the damping ( D ), the capacitance C , the mechanical compliance ( δ ), this size is the reciprocal value of the mechanical stiffness S , and the inductance is determined by the mass M expressed. The mechanical counterpart to the electrical voltage ( U ) is the mechanical force ( F ), the electrical current ( I ) is represented by the speed ( v ).

As in an electrical system, a mechanical impedance ( Z ) as a function of the angular frequency ω can be determined from these analogous relationships , the angular frequency being multiplied by the imaginary unit j. The identifiers x , v , and a stand for the distance x , speed v and acceleration a . In total, the following relationships result:

Mechanical size	relationship	Mechanical impedance	Electrical analog quantity	Electrical impedance
Compliance δ	${\ displaystyle \ delta = {x \ over F}}$	${\ displaystyle Z = {1 \ over \ mathrm {j} \ omega \ delta}}$	Capacity C	${\ displaystyle Z_ {e} = {1 \ over j \ omega C}}$
Mass M	${\ displaystyle M = {\ frac {F} {dv / dt}} = {F \ over a}}$	${\ displaystyle Z = \ mathrm {j} \ omega M \,}$	Inductance L	${\ displaystyle Z_ {e} = \ mathrm {j} \ omega L \,}$
Damping D	${\ displaystyle D = {F \ over v}}$	${\ displaystyle Z = D \,}$	Resistance R	${\ displaystyle Z_ {e} = R \,}$

The table above shows the so-called impedance analogy, with the help of which the mechanical system can be described and calculated like an electrical circuit. This means that the methods of complex alternating current calculations can also be applied directly to the mechanical system. In addition to a damping component due to friction, every mechanical element consists of a mass and a certain stiffness, which, as in electrical circuits, can only be used as an approximation to form concentrated components with one of the desired properties. If the influence of the flexibility over the mass predominates with low damping, "mechanical capacitors" are formed. Typically these consist of thin rods that are as long as possible. “Mechanical coils”, as a counterpart, consist of short, flat discs made of solid material, which maximize their mass and minimize flexibility.

Schematic representations of mechanical filters
Disc-shaped resonators and half-wave connecting elements attached to the edge
Mechanical filter with torsion resonators
Mechanical filter with drumhead resonators
Mechanical filter with flexual resonators

literature

Rüdiger G. Ballas, Günther Pfeifer, Roland Werthschützky: Electromechanical systems in microtechnology and mechatronics . 2nd Edition. Springer, 2009, ISBN 978-3-540-89317-2 .

Individual evidence

^ Joseph J. Carr: RF Components and Circuits . Newnes, 2002, ISBN 0-7506-4844-9 .
^ Frederick V. Hunt: Electroacoustics: the Analysis of Transduction, and its Historical Background. Harvard University Press, Cambridge 1954, OCLC 2042530.

Web links

Commons : Mechanical filters - collection of images, videos and audio files

[carr1-1] Joseph J. Carr: RF Components and Circuits . Newnes, 2002, ISBN 0-7506-4844-9 .

[hunt1-2] Frederick V. Hunt: Electroacoustics: the Analysis of Transduction, and its Historical Background. Harvard University Press, Cambridge 1954, OCLC 2042530.