Frequency spectrum
The frequency spectrum , usually simply spectrum , of a signal indicates its composition from different frequencies . In general, the frequency spectrum is a complex-valued function . Its amount is called the amplitude spectrum , its phase angle is called the phase (angle) spectrum .
The term frequency spectrum encompasses many different phenomena from all areas of physics such as optics, acoustics, electrodynamics or mechanics.
- Light is made up of waves of different frequencies. With the spectrum of light, its color usually changes, see color perception .
- The frequency of a tone determines its pitch . Among other things, the frequency spectrum of the sound characterizes the sound of a musical instrument or a human voice.
- The frequency mix of a broadcast signal contains the picture and sound information.
- The frequency of a mechanical oscillation determines how often the oscillation repeats itself in a certain time. A complicated mechanical vibration is, for example, the deflection of a seismograph during an earthquake . They are made up of vibrations of different frequencies.
The frequency spectrum of a signal can be calculated from the underlying signal by using the Fourier transform . The representation in the frequency domain is used in physics and technology to describe physical processes more simply than by functions of time or place.
Frequency spectrum of a time signal
Due to their frequent use, the class of so-called time signals is described first. The frequency spectrum of a time signal is based on the notion that a time-dependent signal x (t) can be composed as a sum or an integral of complex exponential functions of different frequencies using the transformation rules of Fourier series or Fourier transformation. The complex exponential functions are called "structure functions" in this context. The frequency spectrum describes the weighting (ie strength) with which the structure function associated with the respective frequency is included in the overall signal. The formulas for the inverse Fourier transformation are shown for the mathematical representation of the signal synthesis. To do this, it is necessary to differentiate which type of signal is present.
Periodic signal with a discrete spectrum
If the signal is a time-continuous periodic function with the period , the corresponding equation reads:
The equation describes the signal x (t) as a sum of complex exponential oscillations of the frequencies . The function is called the spectrum of the signal x
with the fundamental frequency . The number is representative of n times the basic frequency. The complex exponential oscillation can be described by the equation . Since the spectrum is only defined for the discrete frequencies , one speaks of a discrete spectrum or a line spectrum .
Non-periodic signal with a continuous spectrum
If the signal x (t) is a non-periodic time-continuous function with finite signal energy , the corresponding transformation equation reads:
In this case, the function is called the spectrum of the signal
Since the spectrum is defined for all real-valued frequencies, one speaks of a so-called continuous spectrum. The spectrum of the continuous Fourier transformation can be represented as the limit case of the line spectrum of the Fourier series for the limit transition of an infinitely large signal period.
Explanations and other signal classes
Both frequency spectra are defined for both positive and negative frequencies. For real-valued signals x (t), the spectra for positive and negative frequencies, however, are dependent on one another, and we have: . The asterisk indicates the complex conjugation . As a rule, the spectrum of negative frequencies is therefore only displayed for complex-valued signals.
Within the framework of the theory of Fourier analysis , transformation formulas are also defined for other classes of signals, for example for time-discrete, value-continuous signals, i.e. H. sampled analog signals. The terms frequency spectrum , amplitude spectrum and phase spectrum are defined analogously as complex functions as well as their amounts and phases. The details are presented in the article about the Fourier transform and the links it contains.
In connection with non-periodic power signals such as noise signals, there is the term spectral power density , which, like the frequency spectrum, also describes the spectral composition of a signal. The special feature of non-periodic power signals is that they cannot be Fourier transformed. This can be seen from the fact that the associated transformation integrals diverge. Nevertheless, a connection with the term Fourier transformation can be established, which is important for metrological practice. If the signal is based on an ergodic development process, the spectral power density can approximately be determined by subjecting a partial signal of finite duration of the actually infinitely long signal to a Fourier transformation. The square of the Fourier transform is then approximately proportional to the spectral power density.
Examples
Elementary signals
The spectra of elementary signals are contained in the descriptions of the associated signal transformations, see examples for the Fourier series and examples for the Fourier transformation . As an example, several spectra of simple signals are to be displayed. The fourth example shows the influence of the phase spectrum on a narrowband signal.
Amplitude spectrum of an audio signal
As an example, consider the amplitude spectrum of the following violin tone
The spectrum of the violin tone depends on the time period chosen for analysis. If one looks at a signal excerpt that was recorded while the strings were being struck, one recognizes not only the fundamental frequency of f 0 = 294 Hz but also clear frequency components of the integer multiples . This can be explained by the fact that the string not only vibrates in its fundamental wave, in which the string experiences a deflection along its entire length, but also has additional nodes at 1/2, 1/3, 2/3, 1 / 4, 2/4, 3/4, ... the string length. The oscillation at a multiple of the fundamental is called overtone in musical parlance . The expression of the individual overtones is not only determined by the vibration of the string alone, but also by the overall arrangement of the instrument (string, resonance body, string pressure when bowing or deflection when plucking). In contrast to the signal excerpt during the bowing, the signal excerpt, which takes into account the decay of the tone, does not show any significant overtone components.
Frequency spectrum of light
While in the radio range of the electromagnetic spectrum the frequency spectrum can still be determined from the temporal progression of the electric field strength , this is no longer possible in the spectral range of light , because the frequencies are over 100 terahertz . Usual plots of optical spectra (see spectroscopy ) often have the wavelength of the light or the energy of the light quanta as the x-axis. If, on the other hand, it is the frequency, one speaks of a frequency spectrum. Wavelength spectra are wider at the red end, frequency spectra at the blue end - wider and flatter if the spectrum is represented as spectral intensity per unit of the x-axis.
Spatial frequency spectra
If the underlying signal s does not depend on the time t but on the coordinates of the location, one speaks of a so-called spatial frequency spectrum. Spatial frequency spectra can be one, two or three dimensional, depending on whether one, two or three dimensional structures are being analyzed. They can have both a continuous and a discrete domain of definition.
Examples of structures with a continuous domain are
- the gray value gradient along a line (one-dimensional)
- the gray value curve of a black and white photograph (two-dimensional)
- the intensity distribution of a physical quantity in space (three-dimensional)
Examples of structures with a discrete domain are
- the gray value gradient on discrete points along a line (one-dimensional)
- the gray value curve on discrete points of a black and white photograph (two-dimensional), e.g. B. Pixel graphics
- the point distribution of a crystal lattice in space
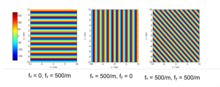
As is analogous in the frequency spectrum of a time function to the spatial frequency spectrum based on the view is that the total signal s (x, y, z) by using the transformation rules of the Fourier series and the Fourier transform as a sum or an integral of complex exponentials of the spatial frequencies , and put together can be .
The exponential function can be illustrated by the location-dependent signal phase. In the case of a two-dimensional transformation, this is shown in the adjacent picture for different spatial frequencies. It can be seen that in general the vector indicates the direction of the maximum phase change.
Non-periodic signal with a continuous spectrum
If the signal s (x, y, z) is a non-periodic time-continuous function of the three position coordinates x, y and z, the corresponding transformation equation reads:
The function is called the spatial frequency spectrum of the signal
Measure the frequency spectrum
The frequency spectrum of an electrical signal can be measured with a spectrum analyzer or signal analyzer . The spectrum is then z. B. determined with the help of Fourier analysis (see also Fourier transformation ) or according to the principle of the heterodyne receiver from the time signal. The result of this transformation is the amplitudes of the respective frequency components A ( f ) as a function of the frequency f and, in the case of amplitude distributions that vary over time, a distribution A ( f, t ) as a function of the frequency f and the time t .
Characteristic spectra
Depending on the number and harmony of the frequencies it contains, the spectrum of a (one-dimensional) audio signal results in a sound (harmonic), a sound mixture (a few inharmonic frequencies), a noise (inharmonic) or a noise (all frequencies, occurring statistically).
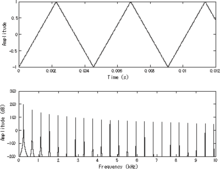
Periodic signals usually have a line spectrum , while non-periodic signals such as pulses have a continuous frequency spectrum .
Examples
- A pure sine wave has only one line of its frequency as the frequency spectrum.
- A square wave signal with frequency f has a line spectrum with frequencies f , 3 · f , 5 · f , ...
- With a pulse generator you can generate all harmonics up to extremely high frequencies.
- A note on a musical instrument always sounds along with its harmonics . The set of all sounding frequencies is the frequency spectrum of this tone.
- An amplitude-modulated radio transmitter (e.g. on medium wave ) that transmits speech and music up to 8 kHz at 1 MHz has a frequency spectrum of 0.992 to 1.008 MHz.
- If the system emits electromagnetic radiation , one speaks of the electromagnetic spectrum .
Other meanings
In a broader sense, frequency spectrum denotes a list of frequencies that have to be seen together in relation to a certain point of view, e.g. B. the frequency spectrum of radio and television channels ; see frequency band .
A response spectrum is used to design structures against the load from earthquakes .
See also
Individual evidence
- ↑ Rüdiger Hoffmann: Signal Analysis and Recognition: An Introduction for Information Technicians, Springer, 1998, p. 69. Quotation in connection with the complex Fourier series: “The series can be interpreted as an orthogonal development of the function x according to the system of structural functions, [... ] "
literature
- Curt Rint : Handbook for high frequency and electrical technicians, Volume 2. 13th edition, Hüthig and Pflaum Verlag GmbH, Heidelberg 1981, ISBN 3-7785-0699-4 .
- Gregor Häberle, Heinz Häberle, Thomas Kleiber: Expertise in radio, television and radio electronics. 3rd edition, Verlag Europa-Lehrmittel, Haan-Gruiten 1996, ISBN 3-8085-3263-7 .
- Horst Stöcker: Pocket book of physics. 4th edition, Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4 .
- Thomas Görne: Sound engineering. 1st edition, Carl Hanser Verlag, Leipzig 2006, ISBN 3-446-40198-9 .