Spectrum analyzer
A spectrum analyzer is a measuring device used in electrical measurement technology to record and display a signal in the frequency range . The display usually takes place on a screen built into the measuring device , the horizontal axis ( abscissa ) being the frequency axis and the amplitude being shown on the vertical axis ( ordinate ). The resulting image is called the frequency spectrum or spectrum for short. In contrast, the measuring device used with a spectrum analyzer, the oscilloscope , displays the signal curve in the time domain . Many digital oscilloscopes now also offer the option of a simple display of the frequency spectrum.
Spectrum analyzers are used in areas such as electrical circuit development and high-frequency technology.
Measurement methods
There are several methods of measuring the complex-valued frequency spectrum from a signal . Since a spectrum analyzer generally cannot establish a time reference to a reference phase and the measured signal and its phase position , only the amount of the frequency spectrum, the so-called amplitude spectrum , is determined and displayed. Some sample spectra including their mathematical description can be found in.
Various measurement methods are common for spectrum analyzers:
- FFT analyzers based on the Fast Fourier Transform ( English Fast Fourier Transform , abbreviated FFT ).
- Analyzers with a bandpass filter that can be tuned over the entire bandwidth .
- Spectrum analyzers based on the heterodyne principle with built-in measuring receivers, mixer stages and intermediate frequency stages .
The procedures are described below. Digital spectrum analyzers may also contain several measurement methods in combination in order to be able to take advantage of the individual methods.
FFT analyzer
The frequency spectrum is calculated directly with the aid of the Fourier transformation (the fast Fourier transformation is used in conventional digital measuring devices). The spectral display in digital oscilloscopes is mostly based on this method. Measurements of this type are (time-domain measurements or time domain methods English Time Domain Measurement ) called.
The advantage is the comparatively low technical effort in the measuring device, the disadvantage is the low achievable bandwidth or, in the case of high bandwidths, the only low spectral resolution with reduced dynamic range . A high dynamic range of 100 dB is only technically feasible up to frequencies of 100 kHz.
The structure of an FFT analyzer is shown in the simplified block diagram. To avoid aliasing, the input signal is subjected to a low-pass filtering and then digitized using an analog-to-digital converter (AD converter). This is followed by storage in a buffer (RAM) and the calculation of the FFT using a suitable window function . Real-time analysis is possible at high signal processing speeds. Due to the property of the block formation, FFT analyzers are only suitable to a limited extent for the analysis of time-strongly changing spectra or pulsed signals.
Detunable bandpass filter
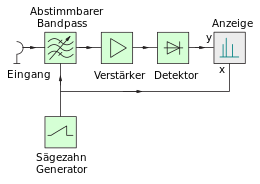
A spectrum analyzer can also be implemented with a tunable bandpass filter directly at the input. The filter's center frequency can be set using a control signal generated by a sawtooth generator. The sawtooth signal serves as a control signal for the automatic sweep over the frequency range to be measured and also serves as a signal for the horizontal deflection (x-axis) in the representation. The bandpass filter only allows the desired section of the frequency range to pass, the signal filtered in this way is amplified and the magnitude value is then generated by the envelope demodulator , symbolized as a diode. The amplitude value formed in this way serves as a vertical deflection (y-axis) in the display.
The difficulty with this analyzer concept is the practical feasibility of narrowband bandpass filters that can be tuned over the entire frequency range. Analog bandpass filters also have an approximately constant relative bandwidth due to their principle. This means that as the center frequency rises, the absolute bandwidth of a bandpass filter increases, which reduces the spectral resolution.
Spectrum analyzers with only tunable bandpass filters are therefore not manufactured as a single analyzer, but only used in combination with other analysis methods. One area of application for input stages is in the frequency range above 3 GHz and usually covers less than half a decade in terms of tunability. At these high frequencies in the microwave range, magnetically tunable YIG filters , based on the material yttrium-iron-garnet , can be technically implemented with appropriate parameters. However, even in this area of application, the filtered input signal is not fed directly to an envelope demodulator, but an intermediate frequency is formed, which is fed to the analysis stages according to the heterodyne principle.
Heterodyne analyzers
In spectrum according to the heterodyne principle, this principle is also used in superheterodyne receivers is used and by a local oscillator (LO) and a mixer stage characterizes the frequency offset. As shown in the schematic diagram opposite, the frequency band to be measured is tuned using a sawtooth generator. The sawtooth signal controls the local oscillator, usually designed as a voltage-controlled oscillator (VCO), which supplies the frequency for the mixer stage located at the input. The mixer converts the input signal to the intermediate frequency.
The intermediate frequency signal formed by the mixer is amplified, fed to a logarithmizer to increase the dynamics and to avoid overdriving , and then the amplitude signal is formed via the envelope demodulator. The logarithmizer also allows the amplitude spectrum to be displayed directly in decibels . The so-called video filter, located directly in front of the display, is an adjustable low-pass filter. The name video filter has historical reasons, it basically serves to reduce noise by averaging the amplitude spectrum. The envelope signal filtered in this way is fed to the display in the vertical direction (y).
Spectrum analyzers that work according to this method have a much more complex structure as a measuring device than in the simplified block diagram. Among other things, several intermediate frequencies are used for this purpose. The first intermediate frequency is usually greater than the highest adjustable measuring frequency in order to ensure uniqueness and to avoid undesired mixed products. In real heterodyne analyzers, this high intermediate frequency is converted to the signal in front of the envelope curve demodulator via additional intermediate frequency stages, usually two further IF stages.
One method of avoiding the high intermediate frequency is a process in which the local oscillator is modulated and the image frequencies are calculated using digital signal processing . This method has a very low level of noise. Devices based on this process move in the upper frequency range, already close to the physical noise limit of −174 dBm / Hz .
The quality of the signal from the local oscillator has a major impact on the quality of the spectrum, as the spectral width of the LO signal as effective magnification of statistical resolution bandwidth RBW ( english resolution bandwidth makes) of the steep-sided as possible IF filter felt. Noise sidebands limit the measurement sensitivity; Relatively slow frequency fluctuations, for example due to small temperature changes, of the local oscillator result in a blurred display and increase the measurement uncertainty .
particularities
Detectors
In the case of spectrum analyzers, detectors that can be selected by the user, in addition to the selection of the filter bandwidths and the selection of window functions, can influence the type of representation of the amplitude spectrum. The detectors, which differ depending on the device, are arranged after the video filter and in front of the display unit and allow, for example, the display of the amplitude spectrum as a peak value such as a maximum or minimum value, as an effective value or as an arithmetic mean value , determined over an adjustable interval range.
Dependencies
In heterodyne analyzers there are dependencies between various adjustable parameters, such as the determined by the sawtooth cycle time ( English sweep time ), the bandwidth of the analog or digital IF stages, the settling time and the bandwidth of the video filter, so it is smaller than the resolution bandwidth. In general, the following relationship applies to the required minimum throughput time :
with as the frequency range to be displayed ( English span ) and the resolution bandwidth of the IF stages. The proportionality factor describes the additional settling time required, is device-dependent and depends on the specific structure of the IF filter stages. The largest possible value of is necessary for the smallest possible transient error . In practice, transient errors around 0.15 dB are tolerated; the usual range of values is from 1 to 2.5. Lower values and shorter processing times are common in digital filter stages with numerical correction of the transient errors in the context of digital signal processing.
To make operation easier, the control software in the measuring devices usually also changes the interdependent variables. For example, if the throughput time and the selected frequency range change, the resolution bandwidth of the filter stages is changed or switched accordingly. In the operating mode with free setting options, and also with historical spectrum analyzers, which in principle do not offer automatic tracking of the dependencies, it is necessary for the user to observe these relationships in order to obtain correct measurement results.
Extensions
In order to be able to record frequency responses of components such as amplifiers or filters directly with a spectrum analyzer , some devices are equipped with a tracking generator , a sinusoidal signal generator which, similar to a wobble generator, provides a frequency of constant signal amplitude synchronously for display. With a spectrum analyzer z. B. also make the frequency response of the components visible. If this system is supplemented by a directional coupler or a circulator , then scalar measurements of the reflection factor can also be carried out on a 1- port . Together with the transmission factor measurement, this enables the basic functionalities of a scalar network analyzer to be simulated with one port. Network analyzers are, however, equipped differently than spectrum analyzers and, as vector network analyzers, can usually also perform the phase profile in addition to the absolute value .
literature
- Christoph Rauscher: Basics of spectrum analysis . 5th edition. Rohde & Schwarz GmbH, Munich 2011, ISBN 978-3-939837-00-8 .
- Joachim Müller: practical introduction to spectrum analysis . beam-Verlag, Marburg 2014, ISBN 978-3-88976-164-4 .
Web links
- Spectrum Analysis Basics, Application Note 150. Agilent Technologies, accessed November 19, 2014 .
Individual evidence
- ↑ Jörg Böttcher: Spectrum of a square wave signal. Retrieved July 2, 2019 .
- ↑ Jörg Böttcher: Further sample spectra. Retrieved July 2, 2019 .