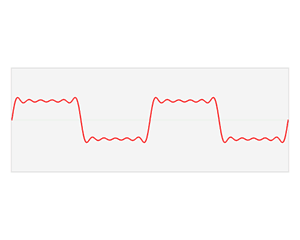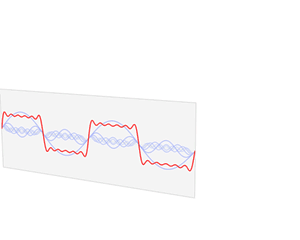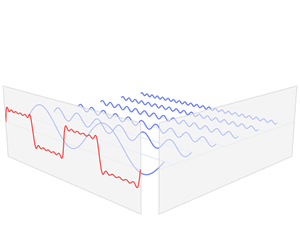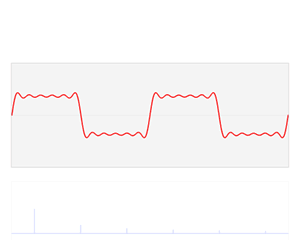
Fourier analysis
The Fourier analysis (pronounced fuʁie ), also known as Fourier analysis or classical harmonic analysis is known, is the theory of Fourier series and Fourier integrals . It is mainly used to break down temporal signals into their frequency components. The signal can be reconstructed from the sum of these frequency components.
Its origins go back to the 18th century. It is named after the French mathematician Jean Baptiste Joseph Fourier , who examined Fourier series in his Théorie analytique de la chaleur in 1822 .
Fourier analysis is of exceptional practical importance in many branches of science and technology. The applications range from physics ( acoustics , optics , tides , astrophysics ) to many sub-areas of mathematics ( number theory , statistics , combinatorics and probability theory ), signal processing and cryptography to oceanography and economics . Depending on the branch of application, the decomposition experiences many different interpretations. In acoustics, for example, it is the frequency transformation of sound into harmonics .
From the perspective of abstract harmonic analysis , both the Fourier series and the Fourier integrals as well as the Laplace transform , the Mellin transform or the Hadamard transform are special cases of a more general (Fourier) transform.
However, Fourier analysis is not limited to time signals. It can also be used for local or other phenomena. For example: A 2-dimensional Fourier analysis is used in image processing (see the relevant paragraph in " Discrete Fourier Transformation "). And the Fourier analysis can also be applied to Fourier spectra themselves in order to recognize periodicities in spectra or other regularities ( see: Cepstrum , Hilbert transformation ).
Variants of the Fourier transform

The various terms in this context are not used uniformly in the literature and there are several names for the same process. Fourier transformation is very often used as a synonym for continuous Fourier transformation, and Fourier analysis often means the decomposition into a Fourier series, but sometimes also the continuous transformation.
Depending on the properties of the function to be examined, there are four variants, as shown in the adjacent figure:
- A continued function which is periodic in a finite interval can be broken down into a Fourier series . The spectrum is therefore discrete.
- A process that extends non-periodically to infinity requires the continuous Fourier transformation (also known as the Fourier integral). A continuous time signal is transformed into a continuous spectrum.
- If only values at discrete , equidistant points in time in a finite interval are known from a process - this interval formation creates a periodic continuation - the discrete Fourier transform (DFT) is used and a discrete frequency spectrum with mirror spectra is created. The DFT and its optimization in the form of the fast Fourier transformation (FFT) play an important role in digital signal processing . An example of such a process is a piece of music from which 44,100 amplitude values of the audio signal are sampled per second at the output of a microphone for storage on a conventional audio CD .
- Related to the DFT is the Fourier transform for time-discrete signals ( English discrete-time Fourier transform , DTFT), which is also based on time-discrete values, but in contrast to DFT, forms a continuous spectrum. It is therefore not directly applicable for spectrum analysis on digital computers, but it is used for the theoretical analysis of signals in the spectrum, since the spectrum can be specified as a closed mathematical expression instead of in a sequence.
With all transformations, a frequency spectrum is obtained that, depending on the variant, is either discrete (infinitely sharp lines) or continuous:
| variant | Definition set of x | Periodicity of x | Frequency spectrum |
|---|---|---|---|
| Fourier series | continuous interval | periodically | discreet |
| Continuous Fourier transform | continuously | aperiodic | continuously |
| Discrete Fourier Transform (DFT) | discreet, finally | aperiodic, continued periodically | discreet, finally |
| Fourier transform for discrete time signals (DTFT) | discreet, finally | aperiodic | continuously |
Fourier series
Every continuously differentiable function that is defined on the interval can be expanded into a Fourier series, that is, both sides of the transformation exist. With the basic frequency and the circular frequencies, the following applies:
- .
More general types of functions can be developed in a Fourier series, such as section-wise continuous, bounded functions or, more generally, measurable square-integrable functions.
Jump point method for polygons
In the case of a periodic polygon (points connected by straight lines), the kinks and any jumps that may be present make the contributions to the Fourier coefficients
- for .
With these and the mean value of a period
the output function can be expressed as the harmonic sum
synthesize. The abscissas of the interpolation values (for jumps: interpolation value pairs and ) must lie in the same period, be ordered in ascending order and fulfill.
The leaps in value
at the jump points , the derivative jumps are calculated as the difference between their right and left-hand limit values or
analogously at the kinks as the difference between the first derivative on the right and left.
The coefficients are times the value; With this calibration of the Fourier coefficients, the amplitudes of the harmonics are equal to the amounts of .
Continuous Fourier transform
The continuous Fourier transform is defined by
The inverse transformation is:
In the literature one can also find other definitions that have 1 as a prefactor instead of just or. This depends on the standardization conventions used. The variant used here has the aesthetic advantage that the prefactor is the same for forward and backward transformation. It also simplifies the representation of Parseval's theorem :
- .
In physics, for example, this condition is important for the conservation of energy through the Fourier transformation. From a mathematical point of view, the equation means that the Fourier transform is a unitary mapping , which is fundamental in quantum mechanics , among other things .
Sometimes, for example in signal theory, one prefers the - also energy-conserving - version of the Fourier transform, in which the Fourier transform - also known as the spectral function - depends on the frequency instead of the angular velocity:
- .
The relationship between the two types of Fourier transform is mediated by.
The inverse transformation is then
- .
Since the variable is instead used for integration, the prefactor is omitted in this form of representation.
Discrete Fourier Transform
There are no restrictions in the application of the transformation and the development formula. If there are positive numbers with , and if there are any integer shifts, a more general variant of the transformation formulas can be specified. With and applies
and
To calculate the discrete Fourier transformation, the fast Fourier transformation (FFT) is often used, an algorithm in which the number of calculation steps for calculating the Fourier coefficients is significantly smaller than with a direct implementation of the integration.
Fourier synthesis
All transformations that are considered in Fourier analysis have the property that a corresponding inverse transformation exists. In engineering , physics and numerical mathematics , the decomposition of a function into its spectrum is also called Fourier analysis. The term therefore not only describes this sub-area of functional analysis, but also the process of decomposing a function. The representation of the output function with the help of the spectrum from the Fourier analysis is called Fourier synthesis. Since this concept formation is particularly common in the applied sciences, it also occurs more in connection with the discrete Fourier transformation and the fast Fourier transformation.
Applications
The Fourier transform has important areas of application , especially in engineering , such as signal processing and physics . Special terms and nomenclatures are also used:
- Time range
- ( English time domain ) If the analysis or representation takes place as a function of time, one speaks of the time domain. If the changeable variable describes a position in space (e.g. in digital image processing ), the area is also referred to as a local area or local area .
- Time signal
- A time signal is the description of the signal curve in the time domain, i. H. as a function of time. The term time signal is also used in connection with the Fourier transform , if one explicitly refers to the inverse transform. I.e. if it is to be clarified that the following description does not refer to the spectrum of the signal.
- Frequency range
- As the frequency domain or space ( English frequency domain ) of the image area after transformation (eg., By Fourier or Laplace transform ) respectively. These names go back to work from the late 1940s at the MIT Research Laboratory of Electronics .
In technically motivated applications, the relationship between the time domain with the original function and the frequency domain with the image function is also shown with the following symbols:
In physics, the Fourier transformation in wave mechanics represents the link between time domain and frequency space. If instead of time signals signals are considered as a function of location, the Fourier transformation is a link between the spatial space and the spatial frequencies or wave numbers present in the frequency space . In several dimensions the wave numbers are described in the form of wave vectors . In crystallography, the frequency space that is reciprocal to location space is called reciprocal space .
In quantum mechanics , except for a proportionality factor, the wave numbers correspond to the momentum of the particle, which results in a connection with Heisenberg's uncertainty principle . Since the spatial and momentum space are linked by the Fourier transformation, the linking of the dimensions leads to a blurring. Analogously, the energy-time uncertainty also results from the Fourier transformation, whereby the frequency here corresponds to the energy except for the proportionality factor and thus a link between energy and time is given by the Fourier transformation, which leads to an uncertainty.
history
As early as 1740, mathematicians such as Bernoulli and d'Alembert discussed the possibility of representing periodic functions as trigonometric series. The series expansion known today for periodic functions goes back to the French mathematician Fourier. At the beginning of the 19th century he published his work Théorie analytique de la chaleur , in which he assumes that every function can be developed into a trigonometric series. He used these series in particular to solve the heat conduction equation . In this work he also introduced the continuous Fourier transformation in the form of a cosine transformation . With this he tried to solve the heat conduction equation on unlimited quantities, especially on the real axis.
Peter Gustav Lejeune Dirichlet investigated these trigonometric series, which are now called Fourier series, and was able to prove the first convergence properties. In 1829 he was able to show that the Fourier series converges point by point if the output function is Lipschitz continuous . For the exact calculation of the Fourier coefficients, Bernhard Riemann then introduced his term integral and discovered the localization principle in 1853. Which states that the convergence or divergence and possibly the value of the Fourier series of a function in the conduct of in an arbitrarily small neighborhood is determined uniquely.
It was not until 1876 that Paul Du Bois-Reymond found a continuous function whose Fourier series does not converge point by point. In its set could Fejér However, in 1904 shows that the Fourier series for each continuous function in the arithmetic mean converges. In 1915 Nikolai Nikolayevich Lusin raised the question of whether the Fourier series converges for every function . This could only be answered positively in 1968 by Lennart Carleson and Hunt generalized the result to functions with in 1968 . However, the prerequisite is essential, as the example of an integrable function with a Fourier series diverging everywhere, which Kolmogorow found in 1926, shows.
Since the Fourier transformation has a large area of application outside of mathematics, one is interested in an algorithm with which a computer can calculate the Fourier coefficients with as little effort as possible. Such procedures are called fast Fourier transforms. The most famous algorithm comes from James Cooley and John W. Tukey , who published it in 1965. However, an algorithm was developed by Carl Friedrich Gauß as early as 1805 . He used it to calculate the trajectories of the asteroids (2) Pallas and (3) Juno . A variant of Carl Runge's algorithm was first published in 1903 and 1905, respectively. In addition, limited variants of the fast Fourier transform were published before Cooley and Tukey. For example, Irving John Good published such an algorithm in 1960.
Math motivation
Mathematical basics
We consider continuous, from the time real-dependent functions or operations (eg. As a vector-valued functions) , which after a time , repeat, so periodic with period are . Joseph Fourier postulated in his work that periodic, harmonic oscillations, i.e. sine or cosine functions, different phases and amplitudes and precisely defined frequencies can be composed. Let us consider such a composite function with summands:
The individual oscillations have the circular frequency , i.e. the frequency . Thus, the first oscillation (fundamental) frequency , the next , ...
Because a sine is only a phase-shifted cosine, the series representation could be restricted to cosine functions. We also get the sine terms immediately if we use the addition theorems :
Together with we get a phase-free representation
In the next step, the sum is to be rewritten with the help of complex numbers . Complex coefficients are then allowed and the series becomes complex-valued. If real-valued functions are considered, this can be recovered as a real part of the sum. From the Euler formula or from the definition of the trigonometric functions with the exponential function follows
- and ,
Consequently
With the complex coefficients , and for n> 0 we get a sum with also negative indices
Fourier series
So we now know the trigonometric sum in different representations. However, it was asked to approximate a periodic continuous function using such a sum. To this end, we note that the complex coefficients , and thus also those of the other representations, can be recovered from the sum function.
To do this, the above equation is multiplied by and then on both sides over the interval , i.e. H. integrated over a period. The following statement can be achieved with forming:
It follows
For the -th integral on the right hand side:
So only the summand for n = 0 makes a contribution, so the integral is simplified to
We can now try to replace the trigonometric sum with any continuous periodic function f , determine the coefficients according to the above formulas, and compare the trigonometric sums formed with these coefficients with the output function:
With the Dirichlet core
Aperiodic processes (Fourier integral)
The prerequisite for the derived Fourier series is the periodicity of over the time interval . Of course, there are also non-periodic functions that do not meet this requirement for a finite time interval. As already shown, the -th harmonic has the frequency . The difference of the -th upper frequency from the previous one is , that is, the upper frequencies have the distance . For towards infinity their distance tends towards zero - in the limit case the sum becomes the Riemann integral .
The Fourier integral, the continuous Fourier transform, is thus given by
With
The result has now become the continuous spectrum . Strictly speaking, the second transformation is called the Fourier transformation, the first, its inverse, is the Fourier synthesis.
The second equation can be derived in the same way as for the series.
The specified relationship pair applies u. a. again for square integrable functions.
Differential equations
The Fourier transform is often used to solve differential equations . Because the or those are eigenfunctions of differentiation, and the transformation converts linear differential equations with constant coefficients into normal algebraic equations.
For example, in a linear time-invariant physical system, the frequency is a conserved quantity, and the behavior can be solved individually for each frequency. Applying the Fourier transform to the differential equation gives the frequency response of the system.
Abstract harmonic analysis
The abstract harmonic analysis is the further development of the Fourier analysis on locally compact topological groups . An integral can be defined on these groups with the help of the Haar measure , which includes the Lebesgue measure as a special case. Central to the abstract harmonic analysis is the concept of character, which was introduced by Lev Semjonowitsch Pontryagin . This is a continuous group homomorphism from the locally compact, Abelian group into the sphere . In analogy to linear functionals and the dual spaces , their totality forms the dual group . The term dual group is justified by the duality principle of Pontryagin . From the point of view of the abstract harmonic analysis, one then understands the figure
the Fourier transform. If you choose and so is and you get the classic continuous Fourier transform. In the abstract harmonic analysis, just like in the classical Fourier analysis, there is also an inverse transformation for this transformation. In addition, this abstract Fourier transform also includes the Fourier series as well as the Laplace transform , the Mellin transform, and other transforms as special cases.
Individual evidence
- ↑ Fourier transformation for time-discrete signals (DTFT) ( Memento of the original from January 24, 2013 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (PDF; 783 kB), student lecture, University of Koblenz-Landau, 2005
- ↑ H. Haase, H. Garbe, H. Gerth: Fundamentals of electrical engineering . Schöneworth Hannover, 2009, ISBN 978-3-9808805-5-8 , pp. 314 ff .
- ↑ Martin Bossert: Introduction to communications engineering . Oldenbourg Wissenschaftsverlag, 2012, ISBN 978-3-486-70880-6 , p. 90-92 .
- ^ YW Lee, TP Cheatham Jr., JB Wiesner: The Application of Correlation Functions in the Detection of Small Signals in Noise. (No longer available online.) In: Technical Report No. 141. MIT Research Laboratory of Electronics, October 13, 1949, archived from the original October 2, 2013 ; Retrieved July 30, 2013 . Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ^ Jean Baptiste Joseph Fourier : Théorie analytique de la chaleur . Chez Firmin Didot, père et fils 1822 ( full text in the google book search).
- ↑ a b c Chr. Schmid: Fourier analysis . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 3-8274-0439-8 .
- ↑ Paul Du Bois-Reymond: Investigations into the convergence and divergence of Fourier formulas , treatises of the mathematical-physical class of the K. Bavarian Academy of Sciences, 1876, Volume 13, pages 1–103
literature
- Rolf Brigola: Fourier Analysis and Distributions . edition swk, Hamburg 2013, ISBN 978-3-8495-2892-8 .
- S. Bochner , K. Chandrasekharan : Fourier Transforms. Princeton University Press, Princeton NJ 1949 ( Annals of mathematics studies 19, ISSN 0066-2313 ).
- Otto Föllinger : Laplace, Fourier and z transformation. Edited by Mathias Kluw. 8th revised edition. Hüthig, Heidelberg 2003, ISBN 3-7785-2911-0 ( studies ).
- Burkhard Lenze: Introduction to Fourier Analysis. 3rd revised edition. Logos Verlag, Berlin 2010, ISBN 3-931216-46-2 .
- MJ Lighthill : Introduction to Fourier Analysis and Generalized Functions. Cambridge University Press, Cambridge 2003, ISBN 0-521-09128-4 ( Cambridge Monographs on Mechanics and Applied Mathematics ).
- Athanasios Papoulis: The Fourier Integral and Its Applications. Reissued. McGraw-Hill, New York NY et al. a. 1987, ISBN 0-07-048447-3 ( McGraw-Hill Classic Textbook Reissue Series ).
- Elias M. Stein , Rami Shakarchi: Princeton Lectures in Analysis. Volume 1: Fourier Analysis. An Introduction. Princeton University Press, Princeton NJ 2003, ISBN 0-691-11384-X .
- Jörg Lange, Tatjana Lange : Fourier transformation for signal and system description. Compact, visual, intuitively understandable. Springer Vieweg 2019, ISBN 978-3-658-24849-9 .
Web links
- Fourier Series Applet - Java applet for demonstrating the Fourier synthesis (English, requires Java).
- Fourier Synthesis - Website to demonstrate Fourier Synthesis (requires JavaScript).
- Lecture notes Applications of the Fourier Transform , Parts 1–6.
- Fourier analysis with mechanical aids
- Fourier and wavelet transformation explained differently
- Sigmar Ries: Fundamentals of the Fourier Transformation. (PDF) Archived from the original on October 2, 2013 ; accessed on November 15, 2014 .
![[0, T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/35ccef2d3dc751e081375d51c111709d8a1d7ac6)