Discrete Fourier Transform
The discrete Fourier transformation (DFT) is a transformation from the field of Fourier analysis . It maps a time-discrete finite signal , which is continued periodically , onto a discrete, periodic frequency spectrum , which is also referred to as the image area . DFT is of great importance in digital signal processing for signal analysis. Here optimized variants in the form are the fast Fourier transform ( english fast Fourier transform , FFT ) used and their inverses.
The DFT is used in signal processing for many tasks, such as: B.
- to determine the frequencies mainly occurring in a sampled signal ,
- to determine the amplitudes and the associated phase relation to these frequencies,
- for the implementation of digital filters with large filter lengths.
With the inverse DFT, iDFT for short , the signal in the time domain can be reconstructed from the frequency components. By coupling DFT and iDFT, a signal can be manipulated in the frequency domain, as it is used with the equalizer . The discrete Fourier transform must be differentiated from the related Fourier transform for discrete-time signals ( discrete-time Fourier transform, DTFT ), which forms a continuous frequency spectrum from discrete-time signals.
definition
Discrete Fourier Transform (DFT)
The discrete Fourier transformation processes a sequence of numbers that have arisen, for example, as time-discrete measured values . It is assumed that these measured values correspond to one period of a periodic signal. The DFT also applies in the event that there is a sequence of complex numbers, i.e.:
The result of the transformation is a breakdown of the sequence into harmonic (sinusoidal) components and a "constant component" which corresponds to the mean value of the input sequence. The result is called the "discrete Fourier transform" of . The coefficients of are the amplitudes of the decomposition components. One also calls Fourier coefficients or Fourier components.
When determining the frequency components / phase position, the compact mathematical notation of the polar form is usually used ( Euler's formula ):
The Fourier coefficients are calculated from the input sequence by:
For
The equation can also be written as a matrix-vector product :
With
The symmetrical transformation matrix with the dimension is called "Fourier Matrix".
Inverse Discrete Fourier Transform (iDFT)
The sum of the sinusoidal decomposition components in turn gives the original input sequence .
For this purpose, the transformation result is used as a coefficient of a polynomial , with the amplitudes representing the associated harmonic oscillations .
The arguments are evenly distributed points on the unit circle of the complex number plane , i.e. H. the –th roots of unity
This explanation also shows the connection between the discrete Fourier transformation and the z transformation . The main difference is that the z-transformation is not limited to the unit circle and can therefore also map temporally dynamic processes.
The coefficients of the original sequence can be determined from the Fourier coefficients with the iDFT :
For
In the notation as a matrix-vector product :
With
where it is multiplied by the inverse matrix of .
Determination of a time-continuous periodic function based on the input sequence
A time-continuous function can also be determined from the inverse discrete Fourier transformation, which leads through the time-discrete measured values (the input sequence):
For this, the polynomial is linked with a function that evenly revolves around the unit circle . This results in a time-continuous periodic function
which at the times just assumes the function values.
The powers of have the shape
and therefore the period and the frequency or the angular frequency . Thus the sequence of the measured values is represented and interpolated by the superposition of a constant level at , a basic oscillation at and harmonics at .
The interpolation function given above is not the only one that can be constructed in this way. Any of the functions
has this interpolation property.
Special case: DFT for a real vector
As with the Fourier transformation, certain laws of symmetry also apply to the DFT. This is how a real signal becomes a Hermitian signal ( ) in the frequency domain:
This means that there are only independent complex coefficients in the frequency domain . This fact can be exploited when implementing the DFT if it is known that the input signal is purely real. For the representation of the result no (as with the full DFT), but only complex numbers are necessary. The other complex numbers can be reconstructed using elementary calculations (see formula above). Hermitian symmetry refers to the middle element of the signal .
-
Proof: Because of Euler's identity and because of the real case :
-
Proof: Because of Euler's identity and because of the real case :
Conversely, the following applies accordingly: If the condition for all and is fulfilled, the inverse DFT is a real vector .
Generalization: Mathematical Definition of DFT
In mathematics , the discrete Fourier transform is viewed in a very general context. Among other things, it is used in computer algebra for a large number of efficient algorithms for exact arithmetic , for example for the rapid multiplication of whole numbers with the Schönhage-Strassen algorithm .
Be a commutative unitary ring in which the number (that is -fold the sum of ) is a unit . Furthermore, there is a primitive -th root of unity . For a tuple the discrete Fourier transform is then by
- For
explained. Under the assumptions made, the discrete inverse Fourier transform with the coefficients also exists
- for .
In the extremely important special case , the -th root of unity is usually used for the DFT . This gives the formula in the first section.
Multi-dimensional DFT
The DFT can easily be extended to multi-dimensional signals. It is then applied once to all coordinate directions. In the important special case of two dimensions ( image processing ), the following applies:
- for and
The inverse transformation is accordingly:
- for and
Shifting and scaling in time and frequency
In the calculation formulas of DFT and iDFT, the summation (index variable above) can run over a shifted range instead of over as well , if the vector is periodically continued to all integer indices, because it applies . So we can move the summation limits arbitrarily as long as a segment of the length in the whole numbers is covered.
Let us now turn back to the complex case. In practical applications one would like to connect the indices with an equidistant sequence of points in time,
- for ,
which also has the length . It is also desirable to assign frequencies to the calculated coefficients that are centered around
- For
and near .
A function “measured” at the selected points in time results in the observation vector with the coefficients , the DFT of which is considered in the Fourier analysis. Then
and
- .
Examples
The Fourier transform transforms a function to a time representation in the reciprocal frequency space . This also applies to position functions that are defined on one (1D), two (2D) or more spatial directions. These are converted into spatial frequencies by the Fourier transformation, one after the other in each direction. Diffraction phenomena in optics or X-ray analysis can be interpreted directly as the intensity distribution of a Fourier transform. The phase relationship is usually lost in photography. Only in the case of holography is the phase relationship recorded by superimposing a reference beam.
Simple bezels
The images on the right illustrate two-dimensional Fourier transforms (2D FFT) on geometric patterns, calculated for squares the discrete size of pixels. The image above left shows a gap the size of pixels, next to it the intensity distribution of the diffraction image . The position variable is converted into reciprocal complex values . With the selected sizes, a pixel is converted to the reciprocal value of reciprocal pixels. The width of the gap of pixels appears in the reciprocal space as a value of the size , the height , with harmonic frequencies of higher order. The calculated diffraction images reflect the intensity distributions of the complex variable . You can tell that they only carry half of the image information by their rotational symmetry.
The periodic peaks correspond to the higher order spatial frequencies of a square wave signal. Similar examples can be found under the keywords Fourier analysis , Fourier transformation or diffraction disks .
A regular hexagon is bent in the second part. Again, the size of the figure appears as a period in the diffraction image on the right. The 6-fold symmetry can be clearly seen. A shift in the original image - as opposed to a rotation - would only have an effect in the phase relationship, which cannot be seen in the selected representation as an intensity distribution.
The lower part shows on the right the calculated diffraction pattern of a triangle. The 6-fold symmetry is only faked, which can be seen from the lack of modulation of the diffraction stars.
The second series of images compares the diffraction of two circular openings. A large circle creates a small diffraction pattern, and vice versa. In a telescope, the diffraction of light at the lens opening limits the resolution. The larger the diameter, the smaller the diffraction pattern of a star, the easier it is to distinguish between stars that are close together.
The picture below is an example of diffraction on a circular structure without a sharp boundary. In the case of a sinusoidal decrease in intensity on the wheel, no higher order diffraction occurs (see also zone plate ).
Image with periodic structures

The image on the left shows a SAR image of the Indian Ocean with water waves of different wavelengths. The internal waves at the top right have a wavelength of approx. 500 m. The surface waves generated by the wind can not be seen in the reduced representation. In the calculated diffraction pattern, the two dark reflections (see short arrow) indicate both the direction and the mean wavelength of the regular long-period water waves. The wavelengths of the surface waves vary more, which is why they do not produce sharp reflections. There are two excellent directions for wave propagation that can only be seen indistinctly in the direct image. The wavelengths are approx. 150 m (long arrow) and 160 m (slightly shorter arrow).
Mathematical basis
The complex numbers that appear in the discrete Fourier transform
are -th roots of unity , d. that is, they are solutions to the equation . Let be the “smallest”, i.e. primitive, root in the first quadrant. This satisfies the following identity of geometric sums of roots of unity
- With
because of for .
This is the "deep reason" why the inverse DFT works.
Let's define in the vectors
- For
so they form an orthonormal basis to the scalar product
- .
It applies
- .
Each vector can be represented in the orthonormal basis:
The coefficients are called Fourier coefficients (also in general for any orthonormal system) , so the DFT assigns the vector of the Fourier coefficients to a vector except for an additive constant .
If with another vector , then Parseval's equation for Fourier coefficients applies :
Interpretations of the DFT
Discretization of the Fourier transform
The Fourier transformation makes it possible to think of functions with real arguments (and various restrictions such as: integrability , periodicity or decay in infinity) composed of vibrations:
An important finding of Fourier theory is that the amplitude can be determined in a similar way
If we choose a radius so large that only an insignificant part of lies outside the interval , it is also continuous and a number is chosen so large that it is small enough to be meaningfully singular, i.e. H. by means of function values , the Fourier integral in the transformation formula can sensibly be replaced by a sum:
With the exception of a constant factor , this corresponds to the DFT calculation formula. The vector has elements. We already know that it is sufficient, the frequency coefficients for the frequencies to determine the function values in the vector to reconstruct. With the necessary adaptation of the constants in the iDFT, we get
The discretization distance in the frequency domain is proportional to , i.e. also small according to the assumption, so that this calculation corresponds to the discretization of the inverse Fourier transform.
In the transition from Fourier transform to DFT, the following changes can be noticed:
- The signal is available at discrete , equidistant points in time ( distance between two successive points in time), is one of these points in time.
- The signal has a finite length ( number of values) which are interpreted as values within a large interval .
- The integrals in the calculation of the Fourier coefficients become sums in DFT.
- The spectrum is only calculated for a finite number of (circular) frequencies with and is periodic in frequency, whereby the period is very large according to the assumption ( small).
Discretization of Fourier series
Every periodic function with a real argument (and again restrictions such as: integrability, no poles) and period can be represented as a series of functions with sinusoids that have fractions of a period (so-called Fourier series ):
- With
If we break off the series expansion at large limits above and below , we get with
d. that is, we get some form of inverse DFT. This means that the coefficients can be approximated to using DFT
In the limit of an infinitely large one , the well-known coefficient integrals of the Fourier series result:
properties
Spectrum of sampled functions
The discrete Fourier transform has a periodic spectrum, it is repeated with the sampling frequency and is symmetrical to the sampling frequency. The following applies:
- (because of natural numbers and )
If the sampled signal contains frequency components above half the sampling frequency, the spectra of the original signal will overlap with the signal components reflected at the sampling frequency, and an aliasing effect will occur.
Aliasing effect
As a rule, the time-discrete signal is created by discretizing a continuous signal. The spectra resulting from the DFT are only identical to the spectra of the underlying continuous signal if the sampling theorem was not violated during the sampling . For signals in the baseband , the sampling frequency must be more than twice as high as the maximum occurring frequency ( Nyquist frequency ). If the sampling theorem is violated, the original signal will be falsified (aliasing in the time domain). One possibility of anti-aliasing is to band-limit the signal at the input of the system in order to avoid this effect.
DFT of a time-limited function
For periodic functions (analogous to the continuous Fourier transformation ) a line spectrum with a frequency line spacing of 1 / period length results .
A time-limited discrete function can be derived from a periodic discrete function by cutting out exactly one period over a time window :
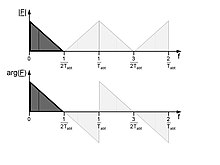
Since in the Fourier transformation a multiplication of functions in the time domain corresponds to a convolution of the Fourier transform in the frequency domain, the DFT of the time-limited function results from the convolution of the DFT of the periodic function with the Fourier transform of the time window :
The result is a line spectrum that is smeared by the Fourier transform of the time window . The influence of the time window on the DFT of the periodic function (thick lines) is shown with a dashed line in Fig. 3. The time limit adds frequency components between the analyzed frequency lines.
Due to the transition from a periodic function to a time-limited function, the calculation method for determining the spectrum does not have to be changed. Furthermore, discrete frequency lines are calculated as if a periodic function were behind them. As an effect of the time window, each calculated frequency line now represents an entire frequency range, namely for the frequency range that has been added by the Fourier transform of the time window. This behavior is also known as the leakage effect.
Leakage effect
Due to the time limit of the signal, the input signal may be cut off. A cut input signal can only be transformed correctly with the DFT if it can be continued periodically. If the signal cannot be continued periodically, it contains frequencies that do not belong to the discrete frequencies calculated by the DFT. The DFT "approximates" these frequencies through the neighboring frequencies, and the energy is distributed to these frequencies. This is known as the leakage effect .
The time limit is equivalent to a multiplication with a rectangular function and corresponds to a convolution with the si function in the frequency domain. This is another way of looking at the leakage effect. This naturally also applies to other window functions (e.g. Hamming, von Hann, Gauss). Thus the spectrum of the window function (or the width of the spectrum) is decisive for the leak. The amplitude accuracy is the other criterion of a window function.
Sliding DFT as a band filter bank
A DFT of a time-limited function can also be viewed as a band filter bank.
- The center frequencies of these band filters correspond to the frequency lines of the function that arises when the observed time segment is repeated periodically (multiples of 1 / window width).
- The width and slope of the band filter is determined by the Fourier transform of the time window (see Fig. 3).
The properties of the band filters can be changed by choosing a suitable time window function.
- In the case of a rectangular time window with discontinuities at the window boundaries, frequencies outside the transmission range of the band filter are attenuated with 1 / frequency; slopes of 6 dB / octave are achieved (see Fig. 2).
- If the window function is continuous, frequencies outside the transmission range of the band filter are attenuated with 1 / frequency 2 ; slopes of 12 dB / octave are achieved.
- If the 1st derivative of the window function is continuous, frequencies outside the transmission range of the band filter are attenuated with 1 / frequency 3 ; the slope is 18 dB / octave.
- etc.
If the Fourier transform of successive time segments is determined, the sliding Fourier transform is obtained. With the analysis of a new time segment, new samples are then obtained for the time course of the spectral lines (that is, the time course of the signals at the outputs of the "band filter").
Uncertainty relation of the sliding DFT
The time and frequency resolution of the sliding DFT cannot be selected independently of one another.
- If you want to analyze signals with a high frequency resolution , you have to make the time window very large, you get a low time resolution.
- If you need a high time resolution, you have to make the width of the time window very short, but then you can only determine a few frequency lines.
- The following applies: Frequency resolution ≈ 1 / time window width (if a frequency resolution of 1 kHz is required, the time window must be at least 1 ms long).
FFT
For block lengths that can be represented as a power of 2, the calculation can be carried out using the fast Fourier transform (FFT) algorithm . In general, the following applies: If the block length can be factored, the DFT of the length is broken down into a product of DFTs of the lengths and two simple matrices.
Goertzel algorithm
The Goertzel algorithm can also be used for any block lengths and to determine a single or a few spectral components . The advantage is a very efficient implementation in computer systems, since the calculation for each spectral component comprises only one complex multiplication and two complex additions.
Applications
- Calculation of the Fourier transform of a signal
- Signal analysis
- Vibration analysis and modal analysis
- Processing of signals
- Calculation of correlations
- Calculation of polynomial products in
For the calculation of surface acoustic wave filters (SAW filters = = = SAW filter surface acoustic wave filters), the inverse Fourier transform is the transfer function required (represents the impulse response group). This task is carried out by computers.
See also
- folding
- Gabor transformation
- Laplace transform
- z transformation
- Discrete cosine transformation
- Wavelet transform
- Window function
- Fourier series
- Short-time Fourier transform
literature
- Tilman Butz: Fourier transformation for pedestrians. 7th edition. Vieweg + Teubner Verlag, Wiesbaden 2011, ISBN 978-3-8348-0946-9 , chapter 4.
- MW Wong: Discrete Fourier Analysis. Birkhäuser Verlag, Basel 2011, ISBN 978-3-0348-0115-7 .











![{\ displaystyle W [k, j] = e ^ {- 2 \ pi \ mathrm {i} \ cdot {\ frac {jk} {N}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e24870bf4c1fcb5d18dfd4fa70868b7633a0da44)










![{\ displaystyle W ^ {- 1} [k, j] = {\ frac {1} {N}} e ^ {2 \ pi \ mathrm {i} \ cdot {\ frac {jk} {N}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8db59a089bd4cd6a2f5557c59442d44dd3fcbd7d)






























































































![{\ displaystyle [-R, R]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/090cf4334b9bfaf16a2418fe7d5f4effeff0fca1)












![{\ displaystyle [-NT, NT]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/674bd28707c1c23a4f9807abcad5f3988a79f420)