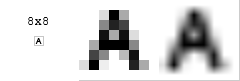Discrete cosine transformation
The discrete cosine transform ( English discrete cosine transform , DCT ) is a transformation of the numerical analysis . She is z. B. used for lossy compression of audio and image data. It is used for image data, for example, in the JPEG compression method; in the area of audio data compression , a modified discrete cosine transformation (MDCT) is used, for example in the context of the AAC format. The discrete cosine transformation was first described in 1974 by Nasir Ahmed, T. Natarajan and KR Rao.
context
The discrete cosine transformation is one of the real-valued , discrete , linear , orthogonal transformations , which, similar to the discrete Fourier transformation (DFT), transforms a time-discrete signal from the time domain (for time signals) or the spatial domain (for spatial signals) into the frequency domain.
Audio and video signals typically have high signal energies in the lower spectral range, for whose decorrelation DCT is particularly well suited and which explains the widespread use of this transformation. Further subordinate applications are the solution of partial differential equations using spectral solution methods. Within the framework of the Chebyshev approximation, the DCT has a mathematical relationship to the Chebyshev polynomials . It is still closely related to the discrete sine transform (DST).
description
Like other discrete frequency transformations, the discrete cosine transformation also expresses a finite input signal sequence as a finite sum of weighted trigonometric functions with different frequencies. Only cosine functions are used for the cosine transformation .
The discrete Fourier transformation, which is defined via a finite input sequence, implicitly also has a definition of how the input data sequence is continued outside of this finite sequence due to the type of transformation and its boundary conditions . In the case of the discrete Fourier transform, this is a periodic continuation; in the case of the discrete cosine transform, this is a straight continuation of the generating signal sequence.
There are different combinations of the type of continuation of the input data sequence and its differentiation into even and odd continuations. There are two edge areas of the input sequence (beginning and end of the sequence), which can be continued evenly or oddly. This results in four different options. It must also be determined from which position in the sequence the continuation must take place. The continuation can take place exactly at the value or between two values. If the continuation is between two values, the first and the last value of the sequence are duplicated. This determination is made separately for the beginning and end of the sequence, which again results in four different combinations. This gives rise to various forms of continuation, i. H. possible forms of the boundary values.
The eight boundary value conditions in the continuation, which have an even continuation at the beginning of a sequence, are counted as part of the discrete cosine transformation, the remaining eight forms with an odd continuation at the beginning of the sequence result in the discrete sine transformation (DST). The various forms are referred to in the literature as DCT-I to DCT-VIII and DST-I to DST-VIII. The four main variants DCT-I to DCT-IV and their continuations in the area of data compression are shown in the figure opposite. The other four variants of the DCT and all 8 variants of the DST are irrelevant in the area of data compression.
These differently continued sequences essentially determine the properties of the individual transformations and their practical significance. When solving partial differential equations by means of spectral transformation, all variants of the DCT or DST are used, depending on the problem. In the area of lossy data reduction of image signals such as JPEG, the DCT-II is used in a two-dimensional transformation, which is why colloquially the "DCT" or the FDCT for forward discrete cosine transform is the type DCT-II. The inversion of the DCT-II is, for reasons of symmetry and except for a constant factor, the DCT-III, also referred to as IDCT for inverse discrete cosine transform (dt. Inverse discrete cosine transformation). In the area of lossy audio signal compression, such as the MP3 file format, a continuous discrete audio data stream must be transformed, whereby the MDCT, which is based on a one-dimensional DCT-IV, is used to avoid aliasing effects in the time domain.
In the area of image and audio compression, the type of continuation and thus the marginal values determine how well the transformation is suitable for data compression. The reason for this is that jumps in the signal sequence lead to high coefficient values in all frequency bands and thus in particular to high-frequency spectral components. This also applies if these jumps occur at the edges of the signal sequence as a result of an unfavorable continuation.
The discrete Fourier transformation is generally a complex-valued transformation and due to the periodic continuation, jumps in the signal curve can occur at the edge points. This also applies to the discrete sine transformation, which has an odd continuation at the beginning of the sequence.
In contrast to the discrete Fourier transform, all forms of the DCT are real transforms and yield real coefficients.
- The DCT transforms signals (e.g. image or audio signals) into their spectral components due to the choice of the type of continuation at the edges.
- The DCT can be efficiently implemented in both software and hardware. There are similar implementations as for the fast Fourier transform (FFT). The DCT calculation can be efficiently implemented using signal processors and their multiply accumulate commands (MAC).
definition
The different types of DCT each map the real-valued input sequence (location or time domain) with elements to a real-valued output sequence (spectral range) :
DCT-I
With regard to its boundary values, the DCT-I is just at the beginning and just at the end .
The DCT-I corresponds, except for a factor of 2, to the DFT of a real sequence of length with even symmetry. For example, the DCT-I of a number-long sequence abcde is identical to the DFT of the sequence abcdedcb up to a factor of 2 . The DCT-I is only defined for sequences with a minimum length of 2; for all other DCT variants, the whole number must be positive.
DCT-II
The DCT-II is the usual DCT. With regard to its boundary values, it is just over at the beginning and just over at the end .
Except for the constant factor 2 of the DFT, the DCT-II corresponds to a real sequence of elements with even symmetry, with all elements with an even index having the value 0.
DCT-III
The DCT-III is the reverse of the DCT-II. With regard to its marginal values, it is even at the beginning and odd at the end . The output sequence is straight at the beginning and straight at the end .
DCT-IV
With regard to its marginal values, the DCT-IV is even at the beginning and odd at the end .
A variant of the DCT-IV is the modified discrete cosine transformation (MDCT), whereby the data sequences of the individual data blocks are overlapped, similar to the overlap-add method , in order to obtain an aperiodic curve.
reversal
Like some other transformations, the DCT can also be reversed. The inverse of the DCT-I is the DCT-I by a factor of . The inverse of the DCT-IV is the DCT-IV with a factor . The inverse of the DCT-II is the DCT-III with a factor of or vice versa.
The pre-factors of the DCT are not standardized in the literature. For example, some authors introduce an additional factor of in DCT in order to avoid the additional factor in inverse surgery. By suitable choice of the constant factor, the transformation matrix can represent an orthogonal matrix .
Multi-dimensional DCT
The two-dimensional DCT, based on the DCT-II, plays an essential role in digital image processing in particular . In the simplest case, expansion to several dimensions is carried out by applying the transformation in columns or rows. For practical implementations, there are more efficient algorithms for calculating higher-dimensional transformations.
The right figure shows as a simple example all spectral components of a two-dimensional DCT-II with eight coefficients in each dimension. The field at the top left (index 0.0) shows the constant component of the signal, in the horizontal direction the horizontal frequency components are increasing. The frequency is doubled across two indices. The same applies to the vertical direction and to the linear combination of the two directions.
Use of 2D DCT
In JPEG, each color component (Y, Cb and Cr) of the image is divided into 8 × 8 blocks which are subjected to 2D DCT.
Use of 3D-DCT
3D-DCT is also sometimes used in film formats. Here is a group of pictures ( group of pictures , GOP) considered multiple images also with regard to the change in time. This method is used, for example, with SoftCast .
Illustrative example of an iDCT
The starting material is an 8 × 8 grayscale image of the letter A.
DCT of the image:
Each individual DCT basic function is multiplied by its current coefficient. The resulting image weighted in this way is added to the finished image.

Left: finished image,
middle: weighting function, which was multiplied by the current coefficient and added to the finished image.
Right: general DCT basic function and the current - related to the example - coefficient
Zoom: 10 × bilinear
The above illustration was enlarged by means of a bilinear zoom. The otherwise square pixels are displayed blurred. The finished image is still an 8 × 8 grayscale image with possibly more or less minimally different color values compared to the original.
literature
- Philipp W. Esslich, Tian Lu: Discrete Orthogonal Transformations . Springer Verlag, 1990, ISBN 3-540-52151-8 .
- Vladimir Britanak, Patrick C. Yip, KR Rao: Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations . 1st edition. Academic Press, 2007, ISBN 978-0-12-373624-6 .
Web links
- taramath online tool for calculating the discrete cosine transformation (DCT-II).
Individual evidence
- ↑ N. Ahmed, T. Natarajan, KR Rao: Discrete Cosine Transform. In: IEEE Trans. Computers. Volume C-23, No. 1, 1974, pp. 90-93, doi: 10.1109 / TC.1974.223784 .
- ↑ S. Jakubczak, D. Katabi: A Cross-Layer Design for Scalable Mobile Video. In: Proceeding MobiCom '11 Proceedings of the 17th annual international conference on Mobile computing and networking. 2011, pp. 289-300, doi: 10.1145 / 2030613.2030646 .



![x [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)
![{\ displaystyle X [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8df678dc1c1a7d63c2dea9e654bd84bc82f772fe)
![x [n] = x_ {0}, \ ldots, x _ {{N-1}} \ Rightarrow X [n] = X_ {0}, \ ldots, X _ {{N-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/839d4790d1902161fb31257d221e3ac11d9439b4)


![X_ {k} = {\ frac {1} {2}} (x_ {0} + (- 1) ^ {k} x _ {{N-1}}) + \ sum _ {{n = 1}} ^ {{N-2}} x_ {n} \ cos \ left [{\ frac {\ pi} {N-1}} nk \ right] \ quad \ quad k = 0, \ dots, N-1](https://wikimedia.org/api/rest_v1/media/math/render/svg/5684c2d94ca9bb311f6c237f967dfed8be63e397)




![X_ {k} = \ sum _ {{n = 0}} ^ {{N-1}} x_ {n} \ cos \ left [{\ frac {\ pi} {N}} \ left (n + {\ frac {1} {2}} \ right) k \ right] \ quad \ quad k = 0, \ dots, N-1](https://wikimedia.org/api/rest_v1/media/math/render/svg/56f0b219e32430b80e09fbd57ae96d172badc5fa)




![X_ {k} = {\ frac {1} {2}} x_ {0} + \ sum _ {{n = 1}} ^ {{N-1}} x_ {n} \ cos \ left [{\ frac {\ pi} {N}} n \ left (k + {\ frac {1} {2}} \ right) \ right] \ quad \ quad k = 0, \ dots, N-1](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad583cf97c5be57ecd96a426be7fef41e7d91e54)
![X_ {k} = \ sum _ {{n = 0}} ^ {{N-1}} x_ {n} \ cos \ left [{\ frac {\ pi} {N}} \ left (n + {\ frac {1} {2}} \ right) \ left (k + {\ frac {1} {2}} \ right) \ right] \ quad \ quad k = 0, \ dots, N-1.](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b8525b68c1a66c043034a098d68695a83fa3432)




![X _ {{k_ {1}, k_ {2}}} = \ sum _ {{n_ {1} = 0}} ^ {{N_ {1} -1}} \ sum _ {{n_ {2} = 0 }} ^ {{N_ {2} -1}} x _ {{n_ {1}, n_ {2}}} \ cos \ left [{\ frac {\ pi} {N_ {1}}} \ left (n_ {1} + {\ frac {1} {2}} \ right) k_ {1} \ right] \ cos \ left [{\ frac {\ pi} {N_ {2}}} \ left (n_ {2} + {\ frac {1} {2}} \ right) k_ {2} \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2d3ec9dcc62ecefe2d1bcc4c043b6fb7d42c484)