Bandwidth

The title of this article is ambiguous. Further meanings are listed under bandwidth (disambiguation) .

The bandwidth is a parameter in signal processing that defines the width of the interval in a frequency spectrum in which the dominant frequency components of a signal to be transmitted or stored are located. The bandwidth is characterized by a lower and an upper limit frequency , whereby different definitions of the two limit values ​​exist depending on the application and thus different bandwidths exist as characteristic values ​​depending on the context. The term is used to describe signal transmission systems in various areas such as communications technology , radio technology or acoustics .

Determinations

Each transmission channel has - depending on its physical properties - a lower and an upper limit frequency. The lower limit frequency can also be zero; in this case one speaks of baseband position , otherwise of bandpass position. The difference in amount between the two limit frequency values ​​is called the bandwidth. The cut-off frequencies are either in the unit Hertz (Hz) and usually abbreviated with f or by means of the angular frequency in the unit s ⁻¹ and referred to as . ${\displaystyle \omega }$

Different definitions are used to define the cut-off frequencies and thus the bandwidth, depending on the application and reference. With identical physical properties, these different definitions can lead to different bandwidth specifications. Some common definitions of the bandwidth are described below.

Strict band limitation

Magnitude frequency response in the baseband with bandwidth ${\displaystyle B}$

A signal is strictly band-limited if the magnitude frequency response , with the parameter as the angular frequency , is equal to 0 outside the range of the bandwidth. In real terms, this is only possible in approximation and the type of bandwidth definition serves as a simplified model in the context of signal theory . ${\displaystyle |X(\mathrm {j} \omega )|}$ ${\displaystyle \omega }$

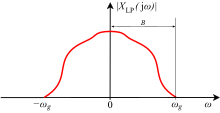
In the case of baseband signals with strict band limitation, the bandwidth is limited by an ideal low pass . Real signals in the baseband position always have negative frequency components , the so-called mirror spectrum , as shown by way of example in the adjacent figure on the absolute frequency profile of a real-valued signal. Without the negative frequency components, the bandwidth is defined as:

${\displaystyle B=\omega _{g}}$

Magnitude frequency response in bandpass position with bandwidth ${\displaystyle B'}$

For signals in the so-called bandpass position, the band is limited by a bandpass filter . Signals in the bandpass position are created, for example, by modulating a baseband signal; they occur, among other things, in intermediate frequency levels in radio devices. The modulation shifts the center frequency of the baseband signal from zero to the carrier frequency , which means that the lower limit frequency has a positive value: ${\displaystyle \omega _{m}}$ ${\displaystyle \omega _{u}}$

${\displaystyle B'=\omega _{g}-\omega _{u}}$

As in the baseband, negative spectral components are not added to the bandwidth. It should be noted that the mirror spectrum of the real-valued baseband signal leads to a doubling of the bandwidth in the bandpass position due to the frequency shift in the case of linear modulation, since the modulation shifts the negative frequencies into the positive spectral range:

${\displaystyle B'=2\cdot B}$

The two positive partial spectra below and above around the center frequency are also referred to as the lower and upper sideband and have the same information content in real-valued baseband signals. For baseband signals that do not have negative frequencies, this is the case with an analytical signal , the bandwidth is identical both in the baseband and in the bandpass position - analytical signals can only be represented as complex signals in the baseband . Technically, this property is implemented in various ways, such as with single sideband modulation . ${\displaystyle \omega _{m}}$

With non-linear modulation techniques such as frequency modulation , there is no direct connection between the bandwidth of the baseband signal and the required bandwidth in the bandpass position. The bandwidth is expressed approximately by the frequency deviation in the Carson formula .

3 dB bandwidth

Power density spectrum of a signal in the baseband position with 3 dB bandwidth ${\displaystyle B}$

Power density spectrum of a signal in the bandpass position with 3 dB bandwidth ${\displaystyle B'}$

In real systems, due to the finite attenuation of filters, spectral components are distributed over the entire spectrum; with a strict definition, the parameter of the bandwidth would be infinitely large and therefore not very meaningful. The usual practical parameter is the 3 dB bandwidth, which is defined by the power density spectrum around the maximum amount . The cut-off frequencies are set at half the maximum power value, which corresponds to a reduction to a rounded 3  dB : ${\displaystyle |X(\mathrm {j} \omega )|^{2}}$ ${\displaystyle A}$ ${\displaystyle A/2}$

${\displaystyle 10\cdot \log {\frac {1}{2}}\approx -3{,}01\,\mathrm {dB} }$

At the cutoff frequency, this corresponds to a reduction in amplitude by the factor . ${\displaystyle 1/{\sqrt {2}}}$

The bandwidth is thus in the baseband position

${\displaystyle B=\omega _{g}}$

and in bandpass position

${\displaystyle B'=\omega _{g}-\omega _{u}}$

set.

For example, in the system of a low-pass filter (1st order), the 3 dB bandwidth corresponds exactly to the bandwidth of the filter; it is therefore also referred to as the 3 dB cutoff frequency . ${\displaystyle B}$

For a series or parallel resonant circuit , the dimensionless relative bandwidth is the ratio of the 3 dB bandwidth and the center frequency : ${\displaystyle d}$ ${\displaystyle B'}$ ${\displaystyle \omega _{m}}$

${\displaystyle d={\frac {B'}{\omega _{m}}}={\frac {1}{Q}}}$

The relative bandwidth is identical to the loss factor and reciprocal to the quality factor Q .

Carson bandwidth

→ Main article : Parameters of frequency modulation

The Carson bandwidth, named after John Renshaw Carson, is used for angle modulations such as frequency modulation or phase modulation . The 10% Carson bandwidth is the bandwidth that spans the spectral lines that make up 90% of the power of the signal; the rarely used 1% Carson bandwidth is the bandwidth in which the spectral lines lie that make up 99% of it. ${\displaystyle B_{10\,\%}}$ ${\displaystyle B_{1\,\%}}$

Nyquist bandwidth

The Nyquist-Shannon sampling theorem has a central position in the theory of digital signal processing . It states that a time-continuous signal can then be reconstructed as precisely as required from the sampled, time-discrete sequence if the bandwidth of the signal is a maximum of half the sampling frequency . This maximum is called the Nyquist bandwidth.

The naive reconstruction as a step function is crude: The rectangular pulses that make up the step function in time, have the sinc function as a spectrum, i.e. an infinite bandwidth. But the bandwidth within the first two zeros of the sinc function (for positive and negative frequencies) is precisely the Nyquist bandwidth. Their product with the sampling period is 1, see time-bandwidth product .

Antenna technology

In the field of antenna technology , among other things, relative, i.e. H. dimensionless, bandwidth specifications used. For narrowband antennas, these are antennas whose frequency response is approximately constant, a percentage bandwidth specification is used:

${\displaystyle B_{\%}=2\cdot {\frac {\omega _{g}-\omega _{u}}{\omega _{g}+\omega _{u}}}}$

The theoretical maximum value of the percentage bandwidth is 200% when the lower limit frequency is zero.

For broadband antennas whose magnitude frequency response is not constant, the two limit frequencies of the antenna are set in relation to each other as a relative bandwidth specification and expressed in the form : ${\displaystyle B_{\text{N}}:1}$

${\displaystyle B_{\text{N}}={\frac {\omega _{g}}{\omega _{u}}}}$

Legal bandwidth specifications

Occupied bandwidth

The term occupied bandwidth, which defines a frequency range that is used by a radio transmission, is particularly common in frequency management . The definition to be seen in the legal context according to Article 1.153 of the Implementing Regulations for the Radio Service (VO Funk) of the International Telecommunication Union (ITU) takes place as integration via the spectral power density , with 99.0% of the total transmitted power within the range between the lower and upper Frequency limit is. The remainder of 1.0% (2 x 0.5%) of the radiated power is outside of this fixed band.

Required bandwidth

The legal definition of the required bandwidth in accordance with Article 1.152 of the Radio Regulations (VO Funk) of the International Telecommunication Union (ITU) is the bandwidth that is just sufficient for a type of transmission at a given speed to ensure the transmission of the message.

Examples of bandwidths

As a first approximation, the transmission system of a telephone has a lower limit frequency of 300 Hz and an upper limit frequency of 3400 Hz, which corresponds to a bandwidth of 3100 Hz and is sufficient for intelligible voice transmission. Frequency components in speech that are below or above the limit frequency are suppressed in a telephone system by means of band limitation and are not transmitted.

application	approximate bandwidth
Nuclear magnetic resonance spectroscopy	0.1 Hz
Longitudinal wave	1 Hz
Electrocardiogram (EKG)	40 Hz
Telephone , slow scan television	3.1 kHz
AM broadcast (audio)	4.5 kHz
AM broadcast signal (broadcast channel width)	9 kHz
analog FM broadcast (audio)	15 kHz
Audio CD	22 kHz
Cellular radio ( GSM ), signal in band pass position	200 kHz
VHF radio signal including additional services, in band pass position	300 kHz
analog AM television signal including sound	7 MHz
digital DVB-T multiplex signal (usually contains four programs)
WLAN according to IEEE-802.11 a / b, bandpass layer	22 MHz
Front side bus in the computer	400 MHz
Ultra broadband	> 500 MHz
Fiber optic ethernet	up to 50 GHz

literature

• Martin Werner: Signals and Systems . 3. Edition. Vieweg Teubner, 2008, ISBN 978-3-8348-0233-0 .
• Karl-Dirk Kammeyer: message transmission . 4th edition. Vieweg Teubner, 2008, ISBN 978-3-8351-0179-1 .
• Michael Dickreiter: Handbook of the recording studio technology . 6th edition. KG Saur Verlag KG, Munich 1997, ISBN 3-598-11320-X .

Individual evidence

1. ^ John R. Carson: Notes on the Theory of Modulation . In: Proceedings of the IRE . tape 10 , no. 1 , 1922, pp. 57-64 .
2. ^ Warren L. Stutzman and Gary A. Theiele: Antenna Theory and Design . 2nd Edition. New York 1998, ISBN 0-471-02590-9 .
3. ↑ Ordinance of the Federal Minister for Science and Transport for the Implementation of the Amateur Radio Act (Amateur Radio Ordinance - AFV), Federal Law Gazette II No. 126/1999, § 1. Definitions, Paragraph (5). Retrieved December 27, 2014 . 
4. ^ VO Funk, Edition 2012, Article 1.153, Definition: occupied (frequency) bandwidth / occupied (frequency) bandwidth
5. ^ VO Funk, 2012 edition, Article 1.152, Definition: necessary bandwidth / required bandwidth

See also

• List of audio terms

Web links

• The -3 dB bandwidth and the quality factor (Q factor)