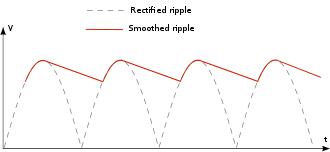
Ripple

If a direct voltage is to be created from a sinusoidal alternating voltage through rectification , a mixed voltage is always created from direct and superimposed alternating voltage. Simple circuits to reduce the AC component use a smoothing capacitor or a smoothing choke , often both together. The fact that a (then mostly undesired) AC voltage component still remains despite the smoothing is referred to as residual ripple . Regulated power supplies and switched-mode power supplies also have a residual ripple, albeit a significantly lower one.

Definitions

Wavy voltage curve (in red) of a rectified alternating voltage (dashed gray) resulting from smoothing

The following definitions apply equally to electrical voltage and current . For the sake of simplicity, this text is limited to the tension.

A mixed variable is made up of a constant component and an alternating component ${\displaystyle u}$

${\displaystyle u=U_{-}+u_{\sim }\ .}$

For the quantitative description of the alternating component, the relevant standard DIN 40110-1 ("Alternating current quantities"; March 1994) specifies three proportions:

• Vibration content as the ratio of the effective value of the alternating component to the effective value of the entire mixed variable  ${\displaystyle U_{\sim }}$ ${\displaystyle U}$

${\displaystyle s_{u}={\frac {U_{\sim }}{U}}\ ,}$

• Waviness as the ratio of the effective value of the alternating component to the amount of the equivalent ${\displaystyle U_{-}}$

${\displaystyle r_{u}={\frac {U_{\sim }}{|U_{-}|}}\ ,}$

• Fluctuation ripple (ripple factor) as the ratio of the oscillation width or peak-valley value (formerly peak-peak value ) to the amount of the equivalent ${\displaystyle {\underset {{}^{\lor }}{\overset {{}_{\land }}{u}}}}$ ${\displaystyle U_{SS}}$

${\displaystyle q_{u}={\frac {\underset {{}^{\lor }}{\overset {{}_{\land }}{u}}}{|U_{-}|}}\ .}$

The vibration content can assume values ​​from 0 (with direct voltage) to 1 (alternating voltage) or 0… 100%.
The ripple and the fluctuation ripple are in the range 0 (direct voltage)… ∞ (alternating voltage).
Occasionally, instead of the waviness , its logarithmic measure is also given. ${\displaystyle r_{u}}$ ${\displaystyle \lg r_{u}\cdot 20{\text{ dB}}}$

The residual ripple is not mentioned in this standard . It is defined as ${\displaystyle \omega }$

${\displaystyle \omega ={\sqrt {F^{2}-1}}\ .}$

The form factor is the ratio of the rms value to the rectified value ${\displaystyle F}$

${\displaystyle F={\frac {U}{\,{\overline {|u|}}\,}}\ ,}$

where in the present context (voltage without change of sign) the rectified value is the same as the amount of the equivalent value. With match the definition of the ripple with the above definition of the ripple of elementary conversion. ${\displaystyle U^{2}={U_{-}}^{2}+{U_{\sim }}^{2}}$

As a parameter for the residual ripple, only the alternating component is sometimes given as an effective value or peak-valley value . Such information is given in millivolts or volts. ${\displaystyle U_{\sim }}$ ${\displaystyle U_{SS}}$

literature

• Andreas Friesecke: The audio encyclopedia. A reference work for sound engineers, 2nd edition, Walter De Gruyter GmbH, Berlin 2014, ISBN 978-3-11-034013-6 .
• Theodor Wasserrab: Circuit theory of power converter technology. Springer Verlag Berlin / Göttingen / Heidelberg, Berlin 1962.

See also

• Current flow angle
• Ripple current
• Distortion factor

Web links

• Smooth Tension (accessed January 21, 2016)