Saddle point

Saddle point of in (0,0) ${\displaystyle y=x^{3}}$

In mathematics , a saddle point , terrace point or horizontal turning point is a critical point of a function that is not an extreme point . Points of this kind are, as the last name suggests, special cases of turning points . Saddle points, for example, play a major role in the optimization under constraints when using the Lagrange duality .

One-dimensional case

Saddle point of in (0,0) ${\displaystyle y=x\cdot |x|}$

For functions of a variable with the first derivative disappears at the point ${\displaystyle f\colon U\to \mathbb {R} }$ ${\displaystyle U\subseteq \mathbb {R} }$ ${\displaystyle x_{0}}$

${\displaystyle f\,'(x_{0})=0}$

a condition that there is a critical point. If the 2nd derivative is not equal to 0 at this point, there is an extreme point and therefore no saddle point. For a saddle point, the 2nd derivative must be 0 if it exists. However, this is only a necessary condition (for twice continuously differentiable functions), as you can see from the function . ${\displaystyle f(x)=x^{4}}$

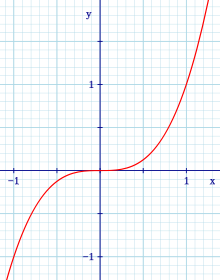
The opposite applies (sufficient condition): If the first two derivatives are equal to 0 and the third derivative not equal to 0, then there is a saddle point; it is therefore a turning point with a horizontal tangent.

This criterion can be generalized: applies to a ${\displaystyle n\in \mathbb {N} }$

${\displaystyle f'(x_{0})=f''(x_{0})=\dotsb =f^{(2n)}(x_{0})=0\wedge f^{(2n+1)}(x_{0})\neq 0,}$

if the first derivatives are equal to 0 and the -th derivative not equal to 0, the graph of at has a saddle point. ${\displaystyle 2n}$ ${\displaystyle (2n+1)}$ ${\displaystyle f}$ ${\displaystyle x_{0}}$

However, this condition is not necessary. Even if there is a saddle point at the point , all derivatives can be zero. ${\displaystyle x_{0}}$ ${\displaystyle f^{(n)}(x_{0})}$

In the one-dimensional case, a terrace point can be interpreted as a turning point with a tangent parallel to the x-axis.

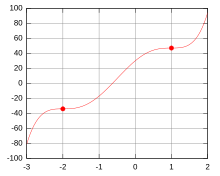
Example of a completely rational function (polynomial function) with two saddle points

fully rational function of the 5th degree with two saddle points in (−2, −34) and (1, 47)

Even fully rational functions of the 5th degree can have two saddle points, as the following example shows:

${\displaystyle f(x)=2x^{5}+5x^{4}-10x^{3}-20x^{2}+40x+30}$

Because the 1st derivative has two double zeros −2 and 1:

${\displaystyle f'(x)=10x^{4}+20x^{3}-30x^{2}-40x+40=10(x+2)^{2}(x-1)^{2}}$

For the 2nd derivative

${\displaystyle f''(x)=40x^{3}+60x^{2}-60x-40}$

are −2 and 1 also zeros, but is the 3rd derivative

${\displaystyle f'''(x)=120x^{2}+120x-60}$

there not equal to zero:

${\displaystyle f'''(-2)=f'''(1)=180}$

Therefore and are saddle points of the function . ${\displaystyle S_{1}(-2|-34)}$ ${\displaystyle S_{2}(1|47)}$ ${\displaystyle f}$

Multi-dimensional case

Saddle point (red) in the case ${\displaystyle U\subseteq \mathbb {R} ^{2}}$

Specification via derivatives

For functions of several variables ( scalar fields ) with the gradient disappears at the point ${\displaystyle F\colon U\to \mathbb {R} }$ ${\displaystyle U\subseteq \mathbb {R} ^{n}}$ ${\displaystyle x_{0}}$

${\displaystyle \nabla F({\vec {x}}_{0})=0}$

a condition that there is a critical point. The condition means that at that point all partial derivatives are zero. If the Hessian matrix is ​​also indefinite , there is a saddle point. ${\displaystyle {\vec {x}}_{0}}$

Specification directly via the function

In the generic case - this means that the second derivative does not vanish in any direction or, equivalently, the Hessian matrix is ​​invertible - the area around a saddle point has a special shape. In the event that such a saddle point with the coordinate axes aligned, can be a saddle point also describe very easily without derivatives: A point is a saddle point of the function if an open environment of there, so ${\displaystyle (x^{*},y^{*})\in U}$ ${\displaystyle F}$ ${\displaystyle V\subseteq U}$ ${\displaystyle (x^{*},y^{*})}$

Play media file

Saddle point in three-dimensional space (animation)

${\displaystyle F(x,y^{*})\leq F(x^{*},y^{*})\leq F(x^{*},y)}$ or. ${\displaystyle F(x^{*},y)\leq F(x^{*},y^{*})\leq F(x,y^{*})}$

is fulfilled for all . This clearly means that the function value of in -direction becomes smaller as soon as the saddle point is left, while leaving the saddle point in -direction results in an increase in the function (or vice versa). This description of a saddle point is the origin of the name: A riding saddle tilts downwards perpendicular to the horse's spine , so it represents the direction, while it is in the direction, i.e. H. parallel to the spine, shaped upwards. The mountain saddle is named after the riding saddle , the shape of which also corresponds to the surroundings of a saddle point. ${\displaystyle (x,y)\in V}$ ${\displaystyle F}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle F}$ ${\displaystyle x}$ ${\displaystyle y}$

If the saddle point is not aligned in the coordinate direction, the above relationship is established after a coordinate transformation .

Saddle points of this type do not exist in dimension 1: If the second derivative does not disappear here, there is automatically a local maximum or a local minimum. The examples from dimension 1 correspond to degenerate critical points, such as the zero point for the function or for : In both cases there is a direction in which the second derivative vanishes, and accordingly the Hessian matrix is ​​not invertible. ${\displaystyle f(x,y)=x^{2}}$ ${\displaystyle f(x,y)=x^{2}+y^{3}}$

Examples

The function

${\displaystyle F(x,y)=(1-x^{2})\left(1+{\frac {1}{4}}(y-1)^{2}\right)\quad {\textrm {in}}\quad \{(x,y)\in \mathbb {R} \times [0,\infty )\}}$

has the saddle point : is , so is for everyone . For results ${\displaystyle (0,1)}$ ${\displaystyle y=1}$ ${\displaystyle F(x,1)=1-x^{2}\leq 1=F(0,1)}$ ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle x=0}$

${\displaystyle F(0,y)=1+{\frac {1}{4}}(y-1)^{2}\geq 1=F(0,1)}$.

That a saddle point is from can also be proven using the derivation criterion. It is ${\displaystyle (0,1)}$ ${\displaystyle F}$

${\displaystyle \nabla F(x,y)=\left[-2x\left(1+{\frac {1}{4}}(y-1)^{2}\right),(1-x^{2}){\frac {y-1}{2}}\right],}$

and after inserting results . The Hessian matrix is closed ${\displaystyle (x,y)=(0,1)}$ ${\displaystyle \nabla F(0,1)={\vec {0}}}$ ${\displaystyle F}$

${\displaystyle H(x,y)={\begin{pmatrix}-2-{\frac {(y-1)^{2}}{2}}&-x(y-1)\\-x(y-1)&{\frac {1-x^{2}}{2}}\end{pmatrix}}}$,

and after inserting the saddle point : ${\displaystyle (x,y)=(0,1)}$

${\displaystyle H(0,1)={\begin{pmatrix}-2&0\\0&{\frac {1}{2}}\end{pmatrix}}.}$

Since one eigenvalue of is positive and one is negative , the Hessian matrix is ​​indefinite, which proves that there is actually a saddle point. ${\displaystyle H}$ ${\displaystyle \left({\tfrac {1}{2}}\right)}$ ${\displaystyle (-2)}$

Other uses

For the definition in the case of systems of ordinary differential equations, see Autonomous Differential Equation .

See also

• Extreme value
• Curve discussion
• Saddle point problem