Pythagorean triple
In number theory , a Pythagorean triple or Pythagorean number triple is formed from three natural numbers that can occur as lengths of the sides of a right triangle . With the side lengths of such a triangle, a right angle can easily be constructed, for example with the smallest triple . Because of the Pythagorean theorem , these triples are exactly the positive integer solutions of the Diophantine equation
- .
If , and have no factor in common except 1, i.e. are coprime pairs , one speaks of a primitive Pythagorean triple.
history

Pythagorean triples can already be found on Babylonian clay tablets , which are dated to the time of the Hammurabi dynasty (1829 to 1530 BC). The cuneiform tablet Plimpton 322 contains 15 different Pythagorean triples, u. a. , and , which suggests that a method for calculating such triples was known more than 3500 years ago. For Egypt, the explicit mention of Pythagorean triples is only possible from a demotic papyrus of the 3rd century BC. Known, but the use in particular of the triplet and for slope angles for some pyramids from a time around two thousand years before the aforementioned papyrus was discussed.
The Indian Baudhayana Sulbasutra from the 6th century BC contains five Pythagorean triples.
Pythagorean triples were treated by Euclid among the Greeks , after Proclus 's commentary on Euclid's elements by Pythagoras and Plato , and later by Diophantus .
Examples
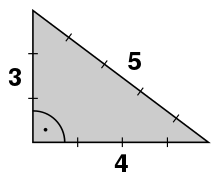
- is the smallest and best known Pythagorean triple. It is primitive because the three natural numbers only have 1 in common as a divisor. When using a twelve-knot cord , the proportions 3: 4: 5 can be used to create a right-angled triangle for the length of the sides and thus represent a right angle .
- and are examples of other small primitive Pythagorean triples.
- Examples of non-primitive Pythagorean triples are with as a common factor or with the common factor .
Primitive Pythagorean triples
Primitive Pythagorean triples are those for which , and have no common factor other than 1 (they are pairwise coprime ).
The primitive Pythagorean triples with are:
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
| (160, 231, 281) | (161, 240, 289) | (68, 285, 293) |
Properties of primitive Pythagorean triples
If , and have no common factor other than 1, one speaks of a primitive Pythagorean triple. For every primitive triple, the product of the pairwise prime numbers is divisible by 3, 4 and 5 as well as odd, and of the numbers and one is even and the other is odd, being composed only of prime factors ( A058529 ). The height given in a right-angled triangle assigned to the primitive Pythagorean triple is irreducible.
Generation of the Pythagorean triples

The symmetry to the 45 ° axis is a consequence of the commutative law .
The formulas
return a Pythagorean triple for any . It is primitive if and only if and are relatively prime and not both are odd.
These formulas were given by Euclid (Elements, Book 10, Proposition 29, Lemma 1). They are sometimes called Indian formulas because they are also explicitly given by the Indian mathematician Brahmagupta (598–668). Possibly they were also known to the Babylonians when they created Pythagorean triples, because the formulas result directly from the Babylonian multiplication formula :
if you bet and .
Conversely, every primitive Pythagorean triple can be generated from coprime ones with the help of these formulas . The height above the hypotenuse of a primitive Pythagorean triangle is always an irreducible fraction due to the pairwise coprime and thus also for coprime different parities. The numerator is always divisible by 12 because a factor can always be divided by 3.
Any Pythagorean triple can be calculated from a primitive Pythagorean triple as having a positive integer . The natural number is the greatest common divisor of and is therefore uniquely determined.
Examples:
- delivers the triple .
- Multiplication with returns . According to the formulas above, because and both are odd, it is not primitive.
- gives the primitive triple
- Multiplication with returns ; this is a Pythagorean triple that cannot be generated with the "Indian formulas". Indeed, these generate all primitive triples, but only part of the non-primitive triples.
The connection of the tree structure of all primitive Pythagorean triples known from B. Berggren (1934) and A. Hall (1970) with the modular group was investigated by RC Alperin (2005). All primitive Pythagorean triples can be generated via seven different linear transformations , each starting from , in exactly three (apart from the arrangement) different ternary root trees , as Firstov generally proved. Exactly one root tree has one linear transformation in common with another, one of which generates, for example, all primitive Pythagorean triples , even all with any odd prime number , and the other root tree discovered by Price uses the two (mixed) representations and the primitive triplet with odd .
Derivation of the formula for the formation of the Pythagorean triples
If a Pythagorean triple results in dividing the associated equation by
The numbers and are rational and positive and satisfy the coordinate equation of the unit circle
So a point with rational coordinates is on the unit circle . The straight line through the points and intersects the y-axis at a point , where the slope of this straight line is, for which applies:
Hence is a rational number.
If one eliminates from this equation and that of the unit circle, one obtains with
a determining equation for .
Because true , so both sides by must divide:
So with that we have
or, because one can set with relatively prime natural numbers :
This gives the Pythagorean triple
It can happen that , and have a common factor . For example , it would follow.
However, the only option for this is to be considered. For suppose an odd prime divided both and so would be
- and
from which, because 2 is prime and 2 is relatively prime , one can further conclude:
The odd prime ie shares and due also . However, this contradicts the coprime numbers of and , so that it cannot be odd. So what remains is what is obviously actually possible and always the case with.
However, one can sort out those that are relatively prime and both odd without losing primitive Pythagorean triples. Because, if and the triple surrender, then surrender and the triple . Here, coprime and not both are odd.
More formulas for Pythagorean triples
According to Proclus, the formulas of Pythagoras and Plato come from antiquity. Pythagoras gives the side lengths for odd , Plato for even the side lengths . If one sets , one can also state the formula of Pythagoras as for .
The first primitive Pythagorean triples
According to the Euclidean rules one obtains as primitive Pythagorean triples for example (ordered according to ):
| u | v | x | y | z |
|---|---|---|---|---|
| 2 | 1 | 3 | 4th | 5 |
| 4th | 1 | 15th | 8th | 17th |
| 3 | 2 | 5 | 12 | 13 |
| 6th | 1 | 35 | 12 | 37 |
| 5 | 2 | 21st | 20th | 29 |
| 4th | 3 | 7th | 24 | 25th |
| 8th | 1 | 63 | 16 | 65 |
| 7th | 2 | 45 | 28 | 53 |
| 5 | 4th | 9 | 40 | 41 |
| 10 | 1 | 99 | 20th | 101 |
| 9 | 2 | 77 | 36 | 85 |
| 8th | 3 | 55 | 48 | 73 |
| 7th | 4th | 33 | 56 | 65 |
| 6th | 5 | 11 | 60 | 61 |
Two sequences of Pythagorean triples are also noteworthy.
-
and results in a triple for every odd number , which contains (as the smallest number) and in which the other two numbers differ by exactly 1. In the right triangle is the half circumference . The height above the hypotenuse cannot be shortened, just like the hypotenuse sections and .
-
and for every number divisible by 4 results in a triple that contains (for as the smallest number) and in which the other two numbers differ by exactly 2. In the right triangle is the half circumference . The height above the hypotenuse cannot be shortened, just like the hypotenuse sections and .
Even if the double of an odd number is still missing , it is easy to always find a (of course not primitive) Pythagorean triple by simply doubling the solutions of the first sequence . Thus one can any natural number a pair of numbers found with which to Pythagorean triples can be supplemented - at odd with the difference 1, straight with differential 2:
| x | y | z |
|---|---|---|
| 3 | 4th | 5 |
| 4th | 3 | 5 |
| 5 | 12 | 13 |
| 6 * | 8 * | 10 * |
| 7th | 24 | 25th |
| 8th | 15th | 17th |
| 9 | 40 | 41 |
| 10 * | 24 * | 26 * |
| 11 | 60 | 61 |
| 12 | 35 | 37 |
| 13 | 84 | 85 |
| 14 * | 48 * | 50 * |
| 15th | 112 | 113 |
| 16 | 63 | 65 |
| 17th | 144 | 145 |
| 18 * | 80 * | 82 * |
| 19th | 180 | 181 |
| 20th | 99 | 101 |
Non-primitive triples are marked with *. The cases for are redundant since they represent a doubling of .
Generalization to Pythagorean ( N + 1) tuples
Pythagorean triples can be understood as points with integer coordinates on a circle with an integer radius. This idea can be generalized to any number of dimensions in such a way that a Pythagorean tuple represents a point with integer coordinates on a -dimensional hypersphere with an integer radius.
All of these -Tuples are solutions of the Diophantine equation , where denotes the radius. For all values of with , for all tuples of integers, there are infinitely many solutions to this equation given by the following identity: with and for all . This results in the sum of squares of whole numbers and thus as a natural number . The proof is done directly by substituting and simplifying:
Proof of identity
This obviously agrees with the right hand side of the equation, which shows the validity of the identity for all -tuples of integers.
Alternative proof
A more convenient notation of the facts and a formulation as a sentence can be obtained by looking at the following figure:
Be as well as: wherein the th component of , the -Einheitsmatrix and the dyadic product of the -th canonical unit vector with the vector designate. Then: . This is clearly a mapping that maps each grid point of a Cartesian grid onto another such grid point - with the property of having an integer Euclidean distance from the origin.
Here too, the proof is provided by simple calculations:
This corresponds precisely to the identity previously proven.
Number of solutions
The number of solutions to the Diophantine equation depends on as well as on. The number of solutions for and can be found in the following table. The number of solutions in dimensions denotes the distance and the total number of all solutions with distance , so the following applies:
| 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | 9 | 10 | Follow in the OEIS | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 6th | 6th | 30th | 6th | 30th | 30th | 54 | 6th | 102 | 30th | A267651 | |
| 8th | 24 | 104 | 24 | 248 | 312 | 456 | 24 | 968 | 744 | A267326 | |
| 6th | 12 | 42 | 48 | 78 | 108 | 162 | 168 | 270 | 300 | A267309 | |
| 8th | 32 | 136 | 160 | 408 | 720 | 1176 | 1200 | 2168 | 2912 | A264390 |
The entries in the sequence are divisible by. Danny Rorabaugh has shown this using the example . The proof can be easily generalized to all .
It is true that the Diophantine equation has only trivial solutions of the form . Interestingly, it must apply so that a nontrivial solution exists for everyone . This follows directly from the four-square theorem of Lagrange , whereafter any natural number (and thus each square number) is represented as the sum of a maximum of four squares, and that the only view of the fact as the sum of square numbers through is provided.
Connection with the Heronian triangles
Every triangle belonging to a Pythagorean triple is a Heronian triangle , that is, both the side lengths and the area are rational numbers. Every Heronian triangle can be broken down into two right-angled triangles, which are given by Pythagorean triples of rational numbers.
The Fermatsche equation
A generalization of the Pythagorean triples is obtained by replacing the exponent 2 with a natural number . So one examines the Diophantine equation
and searches for solutions through natural (or whole) numbers excluding the trivial solutions in which one of the three numbers is equal to zero.
Around 1637, Pierre de Fermat asserted that there are no such triples. Although he gave no proof, this conjecture is called Fermat's Great Theorem . No evidence could be found for centuries. However, the search for it led to many interesting findings, especially in number theory . It was not until 1995 that the mathematician Andrew Wiles was finally able to prove Fermat's theorem.
Fermat had proof of the case and was dealing with the closely related case of a Heronian triangle whose area is a square (see Infinite Descent ). This problem goes back to Diophantus.
algorithm
A possible algorithm in the Haskell programming language could look like this. For a natural number it creates all possible triples whose hypotenuse does not exceed:
pythTripels n = [(k*x, k*y, k*z) | (x,y,z) <- primitives, k <- [1..n`div`z]] where
primitives = [(p^2-q^2, 2*p*q, p^2+q^2) | p <- takeWhile (\p -> p^2+1 <= n) [1..], q <- takeWhile (\q -> p^2+q^2 <= n) [1..p], odd (p+q) && gcd p q == 1]
In Python , List Comprehension is an elegant means of determining Pythagorean triples (example for all triples with c <100):
[(a, b, c) for a in range(1, 100) for b in range(a, 100) for c in range(b, 100) if a ** 2 + b ** 2 == c ** 2]
See also
Web links
- In-depth information on the Pythagorean triplets and proofs
- Eric W. Weisstein : Pythagorean Triple . In: MathWorld (English).
literature
- Peter Bundschuh : Introduction to Number Theory . 6th, revised and updated edition. Springer-Verlag, Berlin a. a. 2008, ISBN 978-3-540-76490-8 .
- Helmuth Gericke : Mathematics in Antiquity, Orient and Occident . Matrix-Verlag, Wiesbaden 2005, ISBN 3-937715-71-1 .
- Georges Ifrah : The Universal History of Computing. From Prehistory to the Invention of the Computer . Translated from the French by David Bellos , EF Harding, Sophie Wood, and Ian Monk. First published in France with the title Histoire universelle des chiffres by Editions Robert Laffont, Paris, in 1994. Harvill Press, London 1998, ISBN 1-86046-324-X .
- Andreas Loos, Hans-Joachim Rein: Triangles with integral side lengths and an interior angle of 60 °, 90 ° or 120 °. In: The mathematical and scientific teaching (MNU). 37th year, 1984, No. 5, pp. 275-279.
- Harald Scheid : Number Theory . 3. Edition. Spectrum Academic Publishing House, Heidelberg u. a. 2003, ISBN 3-8274-1365-6 .
Individual evidence
- ^ Georges Ifrah: The Universal History of Computing. From Prehistory to the Invention of the Computer . S. 151 .
- ^ Corinna Rossi: Mathematics and Architecture in Ancient Egypt. Cambridge UP 2003, p. 217. She cites Richard Parker: Demotic Mathematical Papyri. Brown University Press 1972, pp. 3-4, 35-40.
- ↑ Rossi, loc. cit., p. 219. The Chephren pyramid with an angle of slope of around 53 degrees would therefore be considered for the use of (3, 4, 5), the red pyramid with an angle of slope of around 43 degrees for (20, 21, 29).
- ^ Helmuth Gericke : Mathematics in Antiquity, Orient and Occident . Matrix-Verlag, Wiesbaden 2005, ISBN 3-937715-71-1 , p. 68 .
- ↑ David Joyce: Euclid's Elements.
- ^ Dickson: History of the Theory of Numbers. Volume 2, Carnegie Institution 1920, p. 166.
- ↑ Harald Scheid: Number theory . 3. Edition. Spectrum Academic Publishing House, Heidelberg u. a. 2003, ISBN 3-8274-1365-6 , pp. 225 .
- ^ André Weil: Number theory. An approach through history from Hammurapi to Legendre. Birkhäuser 1984, p. 8. As an alternative, he gives the formula , whereby the Babylonians, according to their number system based on 60, would only have taken products of 2, 3, 5 and would result from systematic trial and error.
- ↑ B. Berggren: Pytagoreiska trianglar. Tidskrift för Elementär Matematik, Fysik och Kemi (in Swedish) 17 (1934), pp. 129-139.
- ^ A. Hall: Genealogy of Pythagorean triads. Math. Gazette 54 (1970), pp. 377-379.
- ^ RC Alperin: The Modular Tree of Pythagoras. (PDF) In: math.sjsu.edu. 2005, accessed June 4, 2020 .
- ↑ VE Firstov: A Special Matrix Transformation Semi Group of Primitive Pairs and the Genealogy of Pythagorean Triples. (PDF) In: mathnet.ru. 2008, accessed May 4, 2020 .
- ^ H. Lee Price: The Pythagorean Tree: A New Species. (PDF; 298 kB) In: arxiv.org. September 2008, accessed February 29, 2020 .
- ^ Frank Bernhart, H. Lee Price: Heron's Formula, Descartes Circles, and Pythagorean Triangles. (PDF; 285 kB) In: arxiv.org. January 1, 2007, accessed February 29, 2020 .
- ↑ The latter formula is already mentioned by Pythagoras (about 570-510 BC); see. Harald Scheid: Number Theory . 3. Edition. Spectrum Academic Publishing House, Heidelberg u. a. 2003, ISBN 3-8274-1365-6 , pp. 225 .
- ↑ sequence A267651 in OEIS






























































![{\ displaystyle {\ begin {aligned} x ^ {2} + t ^ {2} (x + 1) ^ {2} & = 1 \\ (x ^ {2} -1) + t ^ {2} ( x + 1) ^ {2} & = 0 \\ (x + 1) [(x-1) + t ^ {2} (x + 1)] & = 0 \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd1350984a3ac353e0e24b815e105ee492fac84e)













































































































