Heronian triangle

In geometry , a Heronian triangle is understood to be a triangle in which the lengths of the sides and the area are rational numbers . It is named after Heron of Alexandria . Every triangle whose side lengths form a Pythagorean triple is Heronian, since the side lengths of such a triangle are integers and since its area is equal to half the product of the two shorter side lengths. (The inverse of the Pythagorean theorem results in the right angles of the triangle.)

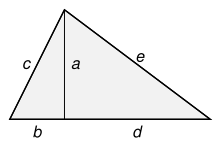
Triangle with sides c , e and b + d and height a

However, a Heronian triangle does not necessarily have to be right angled. This can be seen in the example of the isosceles triangle with side lengths 5, 5 and 6. This triangle can be composed of two congruent right-angled triangles with side lengths . The area is therefore . The example can be generalized easily: Assuming a Pythagorean triple with the largest number and another Pythagorean triple with the largest number, it can, as can be seen from the adjacent drawing, the respective triangles along the two sides with the length to a hero American Put the triangle together. The new triangle has side lengths and . For the area one obtains ${\ displaystyle 3,4,5}$ ${\ displaystyle {\ frac {1} {2}} \ cdot 6 \ cdot 4 = 12}$ ${\ displaystyle (a, b, c)}$ ${\ displaystyle c}$ ${\ displaystyle (a, d, e)}$ ${\ displaystyle e}$ ${\ displaystyle a}$ ${\ displaystyle c, e}$ ${\ displaystyle b + d}$

{\ displaystyle A = {\ frac {1} {2}} (b + d) a}

(half times the base times the height).

It is now interesting to ask whether this procedure, i.e. the joining of two right-angled triangles that coincide in one leg length, gives every Heronian triangle. The answer is no. For example, the Heronian triangle with side lengths and , i.e. the version of the triangle described above that has been shrunk by a factor of 10, of course cannot be broken down into partial triangles with whole-number side lengths. The same applies to the Heronian triangle with the side lengths and the area , since none of the three heights of this triangle is an integer. However, if any rational (i.e. not necessarily natural) numbers are allowed for triples, the question asked can be answered with yes. (Note that any triplet of rational numbers can be obtained by dividing the values of a triplet of integers by the same integer.) ${\ displaystyle 0 {,} 5.0 {,} 5}$ ${\ displaystyle 0 {,} 6}$ ${\ displaystyle 5,29,30}$ ${\ displaystyle 72}$

In a “Heronian triangle”, the tangent of every half (inner) angle is a rational number, as is the sine or cosine of every whole inner angle.

sentence

Every Heronian triangle can be broken down into two right-angled triangles, the side lengths of which are given by Pythagorean triples of rational numbers.

Proof of the theorem

Consider again the above sketch, this time assuming that and the triangular surface are rational. We can assume that the designations were chosen so that the side length is the greatest. This ensures that the solder fell from the opposite corner to this side lies within the triangle. To show that the triples and Pythagorean triples are, one has to prove that and are rational. ${\ displaystyle c, e, b + d}$ ${\ displaystyle A}$ ${\ displaystyle b + d}$ ${\ displaystyle (a, b, c)}$ ${\ displaystyle (a, d, e)}$ ${\ displaystyle a, b}$ ${\ displaystyle d}$

As for the triangular area

{\ displaystyle A = {\ frac {1} {2}} (b + d) a,}

applies, one can resolve and find that way ${\ displaystyle a}$

{\ displaystyle a = {\ frac {2A} {b + d}}}

.

This arithmetic expression is rational because all numbers on the right hand side are rational. So it only remains to show that and are also rational. From the Pythagorean theorem , applied to the two right triangles, one obtains ${\ displaystyle b}$ ${\ displaystyle d}$

{\ displaystyle a ^ {2} + b ^ {2} = c ^ {2} \,}

and

{\ displaystyle a ^ {2} + d ^ {2} = e ^ {2}. \,}

Subtracting these equations gives:

{\ displaystyle b ^ {2} -d ^ {2} = c ^ {2} -e ^ {2} \,}

{\ displaystyle (bd) (b + d) = c ^ {2} -e ^ {2} \,}

{\ displaystyle bd = {\ frac {c ^ {2} -e ^ {2}} {b + d}} \,}

The right hand side of the last equation must be rational, since after the premise and are rational. This proves that is rational. Because of the rationality of this statement follows that and are also rational. ${\ displaystyle c, e}$ ${\ displaystyle b + d}$ ${\ displaystyle bd}$ ${\ displaystyle b + d}$ ${\ displaystyle b}$ ${\ displaystyle d}$

literature

Max Koecher , Aloys Krieg : level geometry . 3. Edition. Springer, Berlin 2007, ISBN 978-3-540-49327-3 .

Web links

Eric W. Weisstein : Heronian Triangle . In: MathWorld (English).
Sascha Kurz: On the Generation of Heronian Triangles . (PDF; 275 kB) Uni-Bayreuth