Height (geometry)

Heights in a triangle ABC:
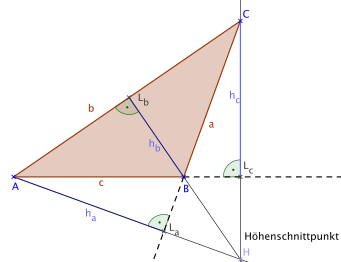
The heights and run outside the triangle because there is an obtuse angle at B. If these heights are extended beyond the corresponding plumb points L _a and L _c and the height beyond corner point B, all three straight lines intersect at the height intersection point H. ${\displaystyle h_{a}}$ ${\displaystyle h_{c}}$ ${\displaystyle h_{b}}$

In geometry, a height is understood as a special perpendicular (perpendicular) to a line or a surface and its length . Heights play an important role in the calculation of areas and volumes ( volumes ). They can also lie outside of figures and bodies , e.g. B. with obtuse triangles . ${\displaystyle h}$

Heights for triangles

If the perpendicular falls from one corner to the opposite side of the triangle, it cuts this side at the base of the perpendicular . The distance between the corner and the plumb line is called the height and the triangle formed by the three plumb points is also known as the height base triangle . Each triangle has exactly three heights. These intersect at a common point, the height intersection . It is inside the triangle for acute triangles and outside the triangle for obtuse triangles. In the case of a right triangle, it coincides with the right-angled corner. The heights of a triangle are also the bisectors of its height base triangle. For the heights , and in a triangle with sides , and denote in the following half the circumference of the triangle, the radii of the inner and circumference and the inner angles in the corner points . The relationship between the sides and heights of the triangle is as follows: ${\displaystyle h_{a}}$ ${\displaystyle h_{b}}$ ${\displaystyle h_{c}}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle s={\frac {a+b+c}{2}}}$ ${\displaystyle r,\,R}$ ${\displaystyle \alpha ,\,\beta ,\,\gamma }$ ${\displaystyle A,\,B,\,C}$

${\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}}$

Beyond this relationship equation, the following applies more precisely:

${\displaystyle {\begin{aligned}h_{a}&={\frac {bc}{2R}}=c\sin(\beta )=b\sin(\gamma )\\h_{b}&={\frac {ac}{2R}}=c\sin(\alpha )=a\sin(\gamma )\\h_{c}&={\frac {ab}{2R}}=b\sin(\alpha )=a\sin(\beta )\\\end{aligned}}}$

This gives the following representation of the product of the three heights:

${\displaystyle h_{a}h_{b}h_{c}={\frac {(abc)^{2}}{8R^{3}}}}$

The relation to the radius of the inscribed circle is:

${\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{r}}}$

With right triangles, Euclid's theorem of heights plays a major role.

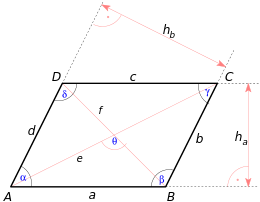
The distance between the two parallels is called the height in the trapezoid

Heights in the parallelogram

Height of trapezoid and parallelogram

• A trapezoid has two opposite sides that are parallel to each other. The distance between these two parallels is called the height of the trapezoid.
• The height of a parallelogram is the vertical distance between the opposite sides.

Heights of other geometric objects

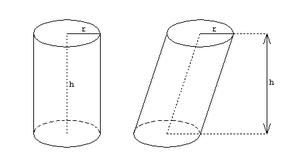
• With prisms and cylinders , the height is the vertical distance between the base and top surface.
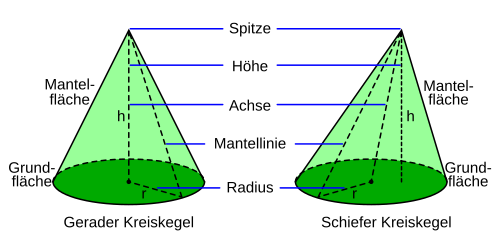
• For pyramids and cones , the height is the perpendicular distance between the tip and the base.
• Also in higher-dimensional geometric objects, such as the hyperpyramid , the (vertical) distance of a corner point in n-dimensional space from a hypersurface lying in a hyperplane is called the height.

literature

• Student dudes: Mathematik I, Dudenverlag, 8th edition, Mannheim 2008, pp. 192–193

Web links

Wiktionary: Height  - explanations of meanings, word origins, synonyms, translations

Wikiquote: Height  - Quotes

• Eric W. Weisstein : Altitude . In: MathWorld (English).
• Heights in the triangle on mathematische-basteleien.de
• All About Altitudes on cut-the-knot.org