Altitude rate
The height set of Euclid , named after Euclid of Alexandria, is a statement of the elementary geometry that in a right-angled triangle between the right angle opposite side and its associated height describes a relationship. Together with the Pythagorean theorem and the cathetus sentence , it forms the so-called Pythagorean sentence group .
Sentence and Applications
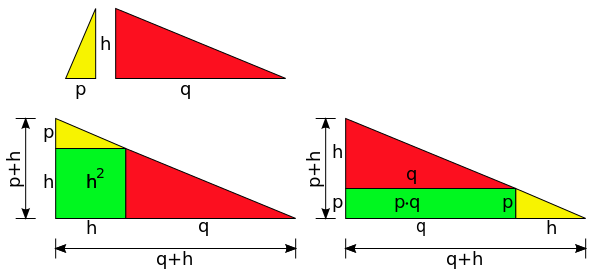
In a right-angled triangle, the height belonging to the hypotenuse divides it into two sections and , the length of the height corresponds to the geometric mean of the lengths of the sections and , that is, the following applies:
- .
The sentence is often expressed as an area rather than a length relation. In this case the area of the height square corresponds to the area of the rectangle formed with the hypotenuse segments and :
- .
The latter illustration provides a method for squaring a rectangle with compasses and ruler , that is, with the aid of the theorem of heights for a given rectangle, an exactly equal square can only be constructed with the aid of compasses and ruler. Proceed as follows (see also the drawing on the right): To a given rectangle with the sides and designate a corner point. Now it extended in the page order , whereby the new route with the length divides. Then you draw a semicircle with as diameter and erect a perpendicular line that intersects the semicircle at the point . According to Thales' theorem, the point and the diameter form a right-angled triangle, the height square of which is the same area as the starting rectangle .
Another application is a geometric proof of the inequality of the arithmetic and geometric mean for two numbers. For the numbers and if you construct a semicircle with a diameter , the height corresponds to the geometric mean and the radius to the arithmetic mean . Since the height is always smaller than or equal to the radius, the validity of the inequality has been shown.
You can set the height as a special case of tendons set conceive. If the first chord corresponds to the diameter of the circle and the second chord is perpendicular to it, then, based on Thales' theorem, its chord segments correspond to the height in a right-angled triangle with the first chord as the hypotenuse. In addition, because of the symmetry of the circle, both chord sections of the second chord are of the same length. In this case, the chord set delivers exactly the equation of the height set.
The reverse of the height rate also applies. If, in any triangle, the height and the side sections created by it and the relationship holds, then the triangle is right-angled.
history
The height theorem is traditionally attributed to the Greek mathematician Euclid, who describes it in its elements . There it is derived as a corollary to Proposition 8 in Book VI. In Proposition 14 in Book II, Euclid also gives a method for squaring a rectangle that essentially corresponds to the method described here. However, Euclid provides a somewhat more complicated proof of their correctness there, since he does not use the height theorem as evidence.
proof
Using similar triangles
Proof of the theorem :
The triangles and are similar as both are similar to the triangle . The latter is the case because they each coincide with the triangle at two angles . The similarity of the two triangles gives the following aspect ratio and the theorem results from an equivalent conversion of the ratio equation:
Proof of the reverse :
Here it has to be shown that any triangle with the property has a right angle in . Because of the equation for height, the following ratio equation also applies . So have the triangles and both a right angle and agree the aspect ratio of the voltage applied to the right angle sides agree. So it follows from the similarity theorems for triangles (SWS theorem) that the two triangles are similar for similar triangles and it applies due to the sum of the angles in the triangle:
About decompositions
The right-angled triangle is cut open along the height and the two partial triangles can then be arranged in two different ways to form a right-angled triangle with the legs and , each of which is missing a third part. In one case the missing section has the area , in the other . Since the two missing pieces complete the partial triangles to form the same triangle, they must have the same area; that is, it applies .
With the Pythagorean theorem
In the configuration of the theorem of heights one has the three right-angled triangles , and , in each of which the Pythagorean theorem applies. This gives:
- and
and thus also
- .
Division by two then yields the height theorem.
About shearings
The height square can be converted into a rectangle of equal area with side lengths p and q by three shears .

literature
- Hartmut Wellstein, Peter Kirsche: Elementary Geometry . Springer, 2009, ISBN 978-3-8348-0856-1 , pp. 76-77
- Euclid : Elements , Book II - Prop. 14, Book VI - Prop. 8, ( online copy (English) )
- Claudi Alsina, Roger B. Nelsen: Pearls of Mathematics: 20 geometric figures as starting points for mathematical exploratory trips . Springer, 2015, ISBN 978-3-662-45461-9 , p. 31
- Fridtjof Toenniessen: The secret of the transcendent numbers: A slightly different introduction to mathematics . Springer, 2009, ISBN 978-3-8274-2275-0 , p. 8
Web links
- The height theorem of the Euclid - materials of the state education server Baden-Württemberg
- Geometric Mean on cut-the-knot.org