Pythagorean quadruple

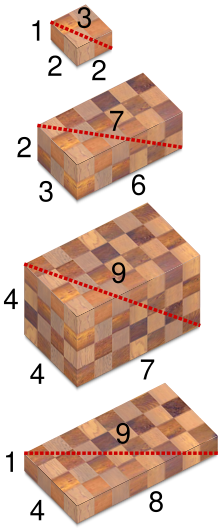
All four primitive Pythagorean quadruples with single-digit values

A Pythagorean quadruple is a tuple of integers such that: ${\displaystyle a,b,c,d\in \mathbb {Z} }$

${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$.

These are the solutions to a Diophantine equation . Most of the time, only positive whole numbers are considered as solutions.

Primitive Pythagorean Quadruples

A Pythagorean quadruple is called a primitive Pythagorean quadruple if the values ​​are positive integers and the greatest common divisor of the four values ​​is 1 (if so ). Each Pythagorean quadruple is an integral multiple of a primitive Pythagorean quadruple. ${\displaystyle (a,b,c,d)}$ ${\displaystyle \operatorname {ggT} (a,b,c,d)=1}$

Example 1:

The tuple is a primitive Pythagorean quadruple because is and holds. ${\displaystyle (a,b,c,d)=(2,3,6,7)}$ ${\displaystyle \operatorname {ggT} (2,3,6,7)=1}$ ${\displaystyle 2^{2}+3^{2}+6^{2}=7^{2}\quad (=49)}$

Example 2:

The tuple is not a primitive Pythagorean quadruple because is, although holds. ${\displaystyle (a,b,c,d)=(5\cdot 2,5\cdot 3,5\cdot 6,5\cdot 7)=(10,15,30,35)}$ ${\displaystyle \operatorname {ggT} (10,15,30,35)=5\not =1}$ ${\displaystyle 10^{2}+15^{2}+30^{2}=35^{2}\quad (=1225)}$

Examples

There are 31 primitive Pythagorean quadruples, all of which have values ​​less than 30:

${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ 1 2 2 3 ${\displaystyle 1^{2}+2^{2}+2^{2}=3^{2}}$ 2 3 6th 7th ${\displaystyle 2^{2}+3^{2}+6^{2}=7^{2}}$ 1 4th 8th 9 ${\displaystyle 1^{2}+4^{2}+8^{2}=9^{2}}$ 4th 4th 7th 9 ${\displaystyle 4^{2}+4^{2}+7^{2}=9^{2}}$ 2 6th 9 11 ${\displaystyle 2^{2}+6^{2}+9^{2}=11^{2}}$ 6th 6th 7th 11 ${\displaystyle 6^{2}+6^{2}+7^{2}=11^{2}}$ 3 4th 12 13 ${\displaystyle 3^{2}+4^{2}+12^{2}=13^{2}}$ 2 5 14th 15th ${\displaystyle 2^{2}+5^{2}+14^{2}=15^{2}}$

${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ 2 10 11 15th ${\displaystyle 2^{2}+10^{2}+11^{2}=15^{2}}$ 1 12 12 17th ${\displaystyle 1^{2}+12^{2}+12^{2}=17^{2}}$ 8th 9 12 17th ${\displaystyle 8^{2}+9^{2}+12^{2}=17^{2}}$ 1 6th 18th 19th ${\displaystyle 1^{2}+6^{2}+18^{2}=19^{2}}$ 6th 6th 17th 19th ${\displaystyle 6^{2}+6^{2}+17^{2}=19^{2}}$ 6th 10 15th 19th ${\displaystyle 6^{2}+10^{2}+15^{2}=19^{2}}$ 4th 5 20th 21st ${\displaystyle 4^{2}+5^{2}+20^{2}=21^{2}}$ 4th 8th 19th 21st ${\displaystyle 4^{2}+8^{2}+19^{2}=21^{2}}$

${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ 4th 13 16 21st ${\displaystyle 4^{2}+13^{2}+16^{2}=21^{2}}$ 8th 11 16 21st ${\displaystyle 8^{2}+11^{2}+16^{2}=21^{2}}$ 3 6th 22nd 23 ${\displaystyle 3^{2}+6^{2}+22^{2}=23^{2}}$ 3 14th 18th 23 ${\displaystyle 3^{2}+14^{2}+18^{2}=23^{2}}$ 6th 13 18th 23 ${\displaystyle 6^{2}+13^{2}+18^{2}=23^{2}}$ 9 12 20th 25th ${\displaystyle 9^{2}+12^{2}+20^{2}=25^{2}}$ 12 15th 16 25th ${\displaystyle 12^{2}+15^{2}+16^{2}=25^{2}}$ 2 7th 26th 27 ${\displaystyle 2^{2}+7^{2}+26^{2}=27^{2}}$

${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ 2 10 25th 27 ${\displaystyle 2^{2}+10^{2}+25^{2}=27^{2}}$ 2 14th 23 27 ${\displaystyle 2^{2}+14^{2}+23^{2}=27^{2}}$ 7th 14th 22nd 27 ${\displaystyle 7^{2}+14^{2}+22^{2}=27^{2}}$ 10 10 23 27 ${\displaystyle 10^{2}+10^{2}+23^{2}=27^{2}}$ 3 16 24 29 ${\displaystyle 3^{2}+16^{2}+24^{2}=29^{2}}$ 11 12 24 29 ${\displaystyle 11^{2}+12^{2}+24^{2}=29^{2}}$ 12 16 21st 29 ${\displaystyle 12^{2}+16^{2}+21^{2}=29^{2}}$

Any number of other non-primitive Pythagorean quadruples can be formed from these primitive Pythagorean quadruples. For example, one can from the primitive Pythagorean quadruple by multiplication by the non-primitive Pythagorean quadruple , , etc. form. ${\displaystyle (a,b,c,d)=(1,2,2,3)}$ ${\displaystyle 2,3,4,\ldots }$ ${\displaystyle (a,b,c,d)=(2,4,4,6)}$ ${\displaystyle (a,b,c,d)=(3,6,6,9)}$ ${\displaystyle (a,b,c,d)=(4,8,8,12)}$

Geometric interpretation

A Pythagorean quadruple defines a parallelepiped with integral side lengths and (with the amount of being meant). The space diagonal of this cuboid then has an integral length . Pythagorean quadruples are therefore also called Pythagorean boxes in English . ${\displaystyle (a,b,c,d)}$ ${\displaystyle |a|,|b|}$ ${\displaystyle |c|}$ ${\displaystyle |a|}$ ${\displaystyle a}$ ${\displaystyle |d|}$

Properties of Pythagorean Quadruples

• The Pythagorean quadruple with the smallest product is . ${\displaystyle (1,2,2,3)}$
• Be with . Then: ${\displaystyle a^{2}+b^{2}+c^{2}=d^{2}}$ ${\displaystyle a,b,c,d\in \mathbb {N} }$

The product is always divisible by. ${\displaystyle abcd}$ ${\displaystyle 12}$

There is no larger number that divides this product, because for the smallest Pythagorean quadruple (i.e. for ) . So there can be no greater number that divides the product. ${\displaystyle (a,b,c,d)=(1,2,2,3)}$ ${\displaystyle 1\cdot 2\cdot 2\cdot 3=12}$

Generation of Pythagorean quadruples

• Method 1:

Be positive integers. Then the set of Pythagorean quadruples with odd can be generated as follows: ${\displaystyle (m,n,p,q)}$ ${\displaystyle a}$

${\displaystyle {\begin{aligned}a&=m^{2}+n^{2}-p^{2}-q^{2},\\b&=2(mq+np),\\c&=2(nq-mp),\\d&=m^{2}+n^{2}+p^{2}+q^{2}\end{aligned}}}$

If the following eleven conditions also apply, then the set of primitive Pythagorean quadruples with odd can be generated. ${\displaystyle a}$

${\displaystyle {\begin{array}{lll}nq>mp,&&m^{2}+n^{2}>p^{2}+q^{2},\\m\geq 0,\;n\geq 1,\;p\geq 0,\;q\geq 1,&&m+p\geq 1,\\m+n+p+q\equiv 1{\pmod {2}},&&{\text{ das heißt, }}m+n+p+q{\text{ ist ungerade (also muss ein Wert oder müssen drei Werte gerade Zahlen sein)}}\\ggT(m^{2}+n^{2},p^{2}+q^{2},mq+np)=1,&&\\m=0\;\Longrightarrow \;q\leq p,&&p=0\;\Longrightarrow \;n\leq m\end{array}}}$

All primitive Pythagorean quadruples thus satisfy the Diophantine equation , which is also called Lebesgue's identity : ${\displaystyle d^{2}=a^{2}+b^{2}+c^{2}}$

${\displaystyle (m^{2}+n^{2}+p^{2}+q^{2})^{2}=(m^{2}+n^{2}-p^{2}-q^{2})^{2}+(2mq+2np)^{2}+(2nq-2mp)^{2}}$

Example 1:

Be and . Then all additional conditions are met and it is and and actually is a primitive Pythagorean quadruple. ${\displaystyle m:=1,n:=7,p:=2}$ ${\displaystyle q:=5}$ ${\displaystyle a=21,b=38,c=66}$ ${\displaystyle d=79}$ ${\displaystyle a^{2}+b^{2}+c^{2}=21^{2}+38^{2}+66^{2}=79^{2}=d^{2}\quad (=6241)}$

Example 2:

Be and . Then the additional condition is not fulfilled, but and because of it it is still a Pythagorean quadruple, but with . ${\displaystyle m:=2,n:=3,p:=5}$ ${\displaystyle q:=9}$ ${\displaystyle m^{2}+n^{2}=13{\stackrel {!}{>}}106=p^{2}+q^{2}}$ ${\displaystyle a=-93,b=66,c=34}$ ${\displaystyle d=119}$ ${\displaystyle a^{2}+b^{2}+c^{2}=(-93)^{2}+66^{2}+34^{2}=119^{2}=d^{2}\quad (=14161)}$ ${\displaystyle a=-93<0}$

Example 3:

Be and . Then is and and actually is . However, this Pythagorean quadruple is not primitive because and is the condition . ${\displaystyle m:=1,n:=3,p:=1}$ ${\displaystyle q:=2}$ ${\displaystyle a=5,b=10,c=10}$ ${\displaystyle d=15}$ ${\displaystyle a^{2}+b^{2}+c^{2}=5^{2}+10^{2}+10^{2}=15^{2}=d^{2}\quad (=225)}$ ${\displaystyle \operatorname {ggT} (a,b,c,d)=5\not =1}$ ${\displaystyle \operatorname {ggT} (m^{2}+n^{2},p^{2}+q^{2},mq+np)=5\not =1}$

• Method 2:

All Pythagorean quadruples (including the non-primitive) can be generated from two positive integers and as follows : ${\displaystyle a}$ ${\displaystyle b}$

Let the parity of and be different (so be either even and odd or odd and even). Furthermore, be a factor of with . Then: ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle p}$ ${\displaystyle a^{2}+b^{2}}$ ${\displaystyle p^{2}<a^{2}+b^{2}}$

${\displaystyle c={\frac {a^{2}+b^{2}-p^{2}}{2p}}}$and with ${\displaystyle d={\frac {a^{2}+b^{2}+p^{2}}{2p}}}$ ${\displaystyle p=d-c}$

Example:

Be and . Then all the conditions are met and it is and (and it is ) and actually is . ${\displaystyle a:=2,b:=11}$ ${\displaystyle p:=5}$ ${\displaystyle c=10}$ ${\displaystyle d=15}$ ${\displaystyle p=d-c}$ ${\displaystyle a^{2}+b^{2}+c^{2}=2^{2}+11^{2}+10^{2}=15^{2}=d^{2}\quad (=225)}$

• Method 3:

Be and both even numbers. Also , be, and a factor of with . Then: ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle l={\frac {a}{2}}}$ ${\displaystyle m={\frac {b}{2}}}$ ${\displaystyle n}$ ${\displaystyle l^{2}+m^{2}}$ ${\displaystyle n^{2}<l^{2}+m^{2}}$

${\displaystyle c={\frac {l^{2}+m^{2}-n^{2}}{n}}}$ and ${\displaystyle d={\frac {l^{2}+m^{2}+n^{2}}{n}}}$

This method generates all Pythagorean quadruples exactly once when and iterates over all pairs of natural numbers and iterates over all possible values ​​for each pair. ${\displaystyle l}$ ${\displaystyle m}$ ${\displaystyle n}$

Example:

Be and . Then all the conditions are met , and it is and and actually is . ${\displaystyle a:=14,b:=6}$ ${\displaystyle n:=2}$ ${\displaystyle l=7}$ ${\displaystyle m=3}$ ${\displaystyle c=27}$ ${\displaystyle d=31}$ ${\displaystyle a^{2}+b^{2}+c^{2}=14^{2}+6^{2}+27^{2}=31^{2}=d^{2}\quad (=961)}$

• There is no Pythagorean quadruple, in which more than one of the numbers , , is odd. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

See also

• Pythagorean triple
• Three squares set

Web links

• Robert D. Carmichael : Diophantine Analysis. Mathematical Monographs , 1915, pp. 1–100 , accessed October 18, 2019 . 
• Eric W. Weisstein : Pythagorean Quadruple. Wolfram MathWorld , accessed October 18, 2019 . 

Individual evidence

1. ↑ To the spelling: In the current Duden - The large dictionary of the German language in ten volumes - ISBN 3-411-70360-1 the adjective "Pythagorean" is given in this spelling and the spelling "Pythagorean" is designated as an Austrian special form.
2. ↑ ^{a b} Robert Spira : The Diophantine Equation x ² + y ² + z ² = m ² . The American Mathematical Monthly 69 (5), 1962, pp. 360-365 , accessed October 11, 2019 . 
3. ^ Raymond A. Beauregard, ER Suryanarayan: Pythagorean Boxes. Mathematics Magazine 74 (3), June 2001, pp. 222-227 , accessed October 11, 2019 . 
4. ↑ Des MacHale, Christian van den Bosch: Generalizing a result about Pythagorean triples. The Mathematical Gazette 96 (535), March 2012, pp. 91-96 , accessed October 11, 2019 . 
5. ^ Paul Oliverio: Self-Generating Pythagorean Quadruples and n -Tuples. Jefferson High School, Los Angeles, Dec. 1993, pp. 98-101 , accessed October 18, 2019 . 
6. ^ Robert Spira: The Diophantine Equation x ² + y ² + z ² = m ² , Theorem 2. The American Mathematical Monthly 69 (5), 1962, p. 362 , accessed October 11, 2019 . 
7. ↑ Pythagorean Quadruple. GeeksforGeeks - A computer science portal for geeks, accessed October 11, 2019 . 
8. ↑ Eric W. Weisstein : Lebesgue Identity. Wolfram MathWorld , accessed October 18, 2019 . 
9. ↑ Titu Andreescu, Dorin Andrica, Ion Cucurezeanu: An Introduction to Diophantine Equations: A Problem-Based Approach, Theorem 2.2.3. Birkhäuser, p. 79 , accessed on October 18, 2019 .