Tangent space
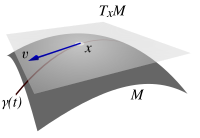
In differential geometry , a tangent space is a vector space that linearly approximates a differentiable manifold at the point . Let be a differentiable curve with and the curve parameter , then:
a tangent vector . The tangent vectors at a point span a vector space, the tangent space . See also tangent bundle .
In algebraic geometry , this definition approach has to be modified to take singular points and changing dimensions into account.
This article deals only with the tangent space over a differentiable manifold in the sense of differential geometry.
Overview
The easiest way to visualize a differentiable manifold, which is embedded as a submanifold in a Euclidean space (e.g. the ). As an example, should sphere (= sphere) in the act. The tangent space in a point is then the plane through the zero point, which is parallel to the tangential plane to the sphere in the point .
A vector field assigns a vector from the associated tangent space to each point of a manifold . For example, a vector field could be used to indicate the wind strength and direction on the earth's surface.
All tangent spaces of a manifold are combined as tangent bundles of ; the tangential bundle is itself a manifold; its dimension is twice that of .
Formal definitions
In the literature it is customary to give three different definitions, which correspond to a geometric, an algebraic and a theoretical-physical ( working towards tensors ) point of view. However, the clear geometric approach proves to be the most difficult to handle in use.
The two algebraic definitions of the tangent space following the geometric definition only work for manifolds of the class , but not for with .
Geometric definition: fields of direction of curves
Given a -dimensional -manifold with , a point from , an open neighborhood of and a map .
Is with a differentiable curve , so is a differentiable curve . So the derivative exists. This derivative is a vector im . Curves that match form an equivalence class . Such an equivalence class is called a tangent vector of in and is written for it . The tangent space is the set of all these tangent vectors; one can show that it does not depend on the choice of card .
It remains to show that by explaining vector addition and scalar multiplication it becomes a vector space . To do this, the mapping is defined by , where the function on the right is any representative of the equivalence class . We now show that this mapping is bijective and, with its help, transfers the vector space operations from to ; one also shows that this construction is independent of the choice of card .
First algebraic definition: generalized derivatives
Be a manifold. A function belongs to the class if it is infinitely differentiable for each card . That so defined is an associative algebra .
Let's fix a point in . A Derivation of a linear map , which for all and in the (analogous to product usually has) following property: . These derivations naturally form a real vector space ; this is the tangent space .
The relationship between the previously defined tangential vectors and the derivatives is as follows: if a curve is with tangential vector , then the corresponding derivation is (with the derivative in the usual sense, since is a function of to ).
Second algebraic definition: dual space of
Be another -manifold and a point in . Now consider the ideal of which consists of all smooth functions is that to represent. Then and are real vector spaces, and is defined as the dual space of the quotient space. is also referred to as the cotangent space (see below ).
While this definition is the most abstract, it is also the one that can most easily be carried over to other situations, for example to varieties such as those considered in algebraic geometry .
Be a derivation . Then for each is in (because it exist with , thus ), which induces a linear mapping . The reverse is a derivation when is a linear mapping. This shows that the via derivations and the tangent space defined via correspond.
Tangent space in algebraic geometry
The two algebraic definitions also work for algebraic varieties, whereby the tangent space is also referred to as the Zariski tangent space . In contrast to manifolds, algebraic varieties can have singularities, where the tangent space then has a higher dimension than in smooth points.
properties
If is an open subset of , then one can naturally consider a manifold. All cards are here the identity, and the tangential spaces are identified with the .
Tangential vectors as direction derivatives
One way of looking at tangent vectors is to see them as direction derivatives. For a vector in defining the directional derivative of a smooth function at a point by
This figure is obviously a derivation. In fact, every derivation of ( ) is of this form. There is a bijection between vectors ( conceived as a tangential vector at the point ) and the derivatives.
Since tangent vectors on a general manifold can be defined as derivatives, it is only natural to see them as directional derivatives as well. Specifically, for a tangential vector of at a point (seen as a derivation) the directional derivative in the direction for element of can be defined as follows:
If we see in the sense of the geometric definition of the tangent space as for a curve , we write
- .
The total derivative of an illustration
Every differentiable mapping between two differentiable manifolds induces a linear mapping
between the corresponding tangent spaces, defined by
for the geometric definition of the tangent space and
for the definition using derivatives.
The linear mapping is called differential , derivative , total derivative or also tangential mapping . Here, too, the notations vary greatly. Are mainly used: , , and .
In a sense, the total derivative is the best linear approximation of in a neighborhood of . The total derivative can be represented as a Jacobian matrix in local coordinates.
If the tangential mapping is surjective, i.e. if the Jacobi matrix has full rank everywhere, the underlying function is called submersion ; the tangential mapping is injective, immersion .
An important result regarding tangential mapping is the theorem :
- If and only if there is a local diffeomorphism at in , is a linear isomorphism .
This is a generalization of the theorem about inverse functions on mappings between manifolds.
Cotangent space
Since the tangent space at the point of the manifold has the structure of a vector space, the dual space can be formed from it. This space is called the cotangent space and is usually noted. According to the last definition, the space is isomorphic to . The cotangent space also plays a very important role in differential geometry. For example, you can use the total differential
- from
understand as a linear mapping, which assigns the directional derivative in its direction to each tangential vector . The total differential is thus an element of the cotangent space of at the point .
literature
- Theodor Bröcker : Analysis. Volume 3. BI-Wissenschafts-Verlag, Mannheim et al. 1992, ISBN 3-411-15851-4 .
- Klaus Jänich : Vector analysis. 5th edition. Springer Verlag, Berlin et al. 2005, ISBN 3-540-23741-0 ( Springer textbook ).
- R. Abraham, Jerrold E. Marsden , T. Ratiu: Manifolds, Tensor Analysis and Applications. Springer-Verlag, Berlin et al. 2003, ISBN 0-201-10168-8 .