Ensemble (physics)

In statistical physics, an ensemble ( listen ^{? / I} ) or a whole is a set of similarly prepared systems of particles in thermodynamic equilibrium . The ensemble is an extremely important term for theory, even though in reality we are usually only dealing with a subset of the ensemble, often with just a single system. Nevertheless, statistical predictions obtained from the ensemble assumption are correct, e.g. B. ensemble mean values , due to the ergodic hypothesis, agree with time mean values ​​of individual systems.

Representation of different ensembles.

Important physical ensembles

Name (alternative name )	given sizes	thermodynamic potential extremalized in equilibrium	inner energy ${\displaystyle U}$	realization	see also	associated state sum
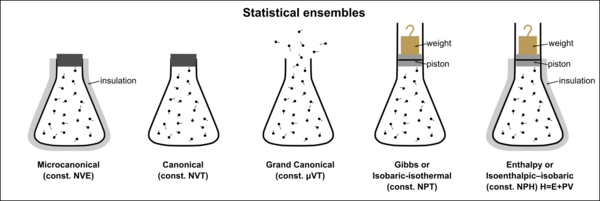
micro-canonical ensemble	${\displaystyle U,V,N}$	Entropy maximum ${\displaystyle S}$	constant	closed systems (idealization)	statistical entropy	micro-canonical ZS
canonical ensemble	${\displaystyle T,V,N}$	free energy minimal ${\displaystyle F}$	${\displaystyle U=TS+F}$	closed systems in the heating bath	Boltzmann statistics	canonical ZS
isothermal-isobaric ensemble (canonical-harmonic ensemble)	${\displaystyle T,p,N}$	free enthalpy minimal ${\displaystyle G}$	${\displaystyle U=TS-pV+G}$	closed systems in the heating bath
grand canonical ensemble (superadditive-canonical ensemble)	${\displaystyle T,V,\mu }$	grand canonical potential minimal ${\displaystyle \Omega }$	${\displaystyle U=TS+\mu N+\Omega }$	open systems in the heat bath		grand canonical ZS

with the given variables

• Internal energy or temperature ${\displaystyle U}$ ${\displaystyle T}$
• Volume or pressure ${\displaystyle V}$ ${\displaystyle p}$
• Particle number or chemical potential per type of particle ${\displaystyle N}$ ${\displaystyle \mu }$
• entropy ${\displaystyle S}$

In the thermodynamic limit (and only then) all thermodynamic ensembles give the same results.

Further thermodynamic ensembles

In addition to the ensembles mentioned above, there are others. One example is the semi-grand canonical ensemble : It is suitable for describing a system made up of several types of particles in which there is a semipermeable membrane that is only permeable to one type of particle.

In the reaction ensemble, fluctuations in the number of particles only occur according to the stoichiometry of the chemical reactions present in the system .

Ensemble in quantum statistics

In quantum statistics , an ensemble denotes the imaginary totality of all systems that result from a certain quantum mechanical preparation process. These systems can each consist of one or more particles.

An interpretation of Heisenberg's uncertainty principle , the ensemble interpretation , is based on ensembles .

The quantum mechanical concept of state is to be seen statistically by its nature . Even with the best possible preparation of a quantum mechanical system, i. H. maximum knowledge in the above sense, the system can be described by a pure state, but even then no statements can generally be made about the outcome of a single experiment . Rather, all statements about the outcome of an experiment are statistical, i.e. H. mean values, standard deviations and other moments of probability distributions are predicted. The origin of this character of quantum mechanics can be seen in Heisenberg's uncertainty relation.

Quantum mechanics therefore does not make any statements about individual measurements on a system, but rather about measurements that are repeated as often as possible under the same preparation conditions . Therefore it is also doubtful whether the term state is permissible as the description of the properties of a concrete individual quantum system. The modern interpretation of quantum mechanics understands this term to mean the totality of very many (ideally any number) under the same conditions independently prepared systems of the same type. This totality is called an ensemble.

The concept of the ensemble now suggests expanding the concept of state in the same way as in statistical mechanics . We see that although every pure state defines an ensemble, not all ensembles of quantum mechanical states can be characterized by pure states. The reason for this lies in the fact that nobody forces the taxidermist in the above scheme to prepare as precisely as possible. The simplest case is e.g. B. that during the preparation, there is a chance with certain probabilities of switching between different "pure" preparations. Such a preparation is called a mixture . Is z. If, for example, there is a mixture of different states in which the pure state was probably prepared, this ensemble is made up of the density matrix ${\displaystyle p_{\mathrm {i} }}$ ${\displaystyle \left|\psi _{i}\right\rangle }$

${\displaystyle \rho =\sum _{\mathrm {i} }p_{\mathrm {i} }\left|\psi _{\mathrm {i} }\right\rangle \left\langle \psi _{\mathrm {i} }\right|}$

described. It should be noted that the individual terms of this sum contain no information about the global phase of the states, i.e. a mixed state is not a coherent superposition of pure states. ${\displaystyle \left|\psi _{\mathrm {i} }\right\rangle }$

In general, it can be shown that every ensemble, especially those that result from poor preparation , can be defined by mixed states . However, in contrast to classical statistical mechanics, such states cannot be clearly broken down into pure states. Different mixtures can define the same state. This is a further reason why it is inadmissible to regard mixed states as an ensemble of pure states, which all describe a single system.

Individual evidence

1. ↑ Basic course Theoretical Physics 6: Statistical Physics, Wolfgang Nolting, Springer DE, 2007, p. 373, Google Books
2. ↑ An Introduction to Applied Statistical Thermodynamics, ISBN 0-470-91347-9 , p. 93, Google Books
3. ↑ Simulation of chemical reaction equilibria by the reaction ensemble Monte Carlo method: a review https://doi.org/10.1080/08927020801986564